Неявные методы решения систем дифференциальных уравнений

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Неявные методы решения дифференциальных уравнений

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

1. Неявные методы

Методы численного решения ОДУ, с которыми мы познакомились в первом разделе этого курса (метод Эйлера, метод средней точки и т. п.), называются «явными» методами. Однако иногда система ОДУ может стать «жесткой», а решать такие системы явными методами неудобно. В этом случае желательно изменить формулировку задачи так, что не пришлось иметь дело с жесткой системой. Но это не всегда возможно, поэтому вы должны уметь решать жесткие ОДУ. Для этого, как правило, используют методы решения, которые называются «неявными».

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

2. Пример жесткого ОДУ

Во-первых, в чем смысл и причина появления жестких уравнений? Давайте рассмотрим пример, который часто возникает в динамике. Предположим, что у нас есть частица, с координатами ((x(t),y(t))) , и предположим, что мы хотим, чтобы ее (y) -координата всегда оставалась равной нулю. Один из способов добиться этого — добавить слагаемое (-ky(t)) , к производной (dot(t)) , где (k) — большая положительная постоянная. Если (k) достаточно велико, то частица никогда не уйдет далеко от (y(t)=0) , так как слагаемое (-ky(t)) всегда приведет (y(t)) обратно к нулю. Предположим далее, что мы хотим, чтобы пользователь мог перемещать частицу как угодно вдоль оси (x) . Дифференциальное уравнение, описывающее движение данной системы, будет иметь вид

(Кроме того, мы предполагаем, что частица не запускается из (y_0=0) ). В результате частица будет сильно притягиваться к прямой (y = 0) , и менее сильно — к (x = 0) . Если решать ОДУ на достаточно продолжительном интервале времени, то частица рано или поздно попадет в точку ((0, 0)) и останется в ней.

Теперь предположим, что для решения уравнения мы используем метод Эйлера. Если сделать шаг размера (h) , то получим

Если мы посмотрим на (у) -компоненту этого уравнения, то увидим, что при (|1-hk|>1) , вычисленное нами (y_) будет по модулю больше, чем (|у_0|) . Другими словами, при (|1-hk|>1) метод Эйлера будет неустойчив: каждый шаг приводит к увеличению (y_) по сравнению с предыдущим значением и приближенное решение будут все дальше отклоняться от нуля. Таким образом, для обеспечения устойчивости метода нужно, чтобы (1-hk>-1) или (hk . Самый большой шаг, который мы можем сделать не нарушив устойчивости, должен быть меньше (2/k) .

Теперь, если (k) – большое число, мы вынуждены делать очень маленькие шаги. Это означает, что частица будет двигаться к ((0,0)) мучительно медленно. Даже если взять (y_0) очень близким к нулю, то придется делать настолько маленькие шаги, что изменение (x) -координаты будет практически незаметно. Вот так выглядит жесткое ОДУ. В данном случае жесткость возникает из-за слишком большого (k) , призванного удержать частицу возле прямой (у = 0) . Позже, когда мы будем рассматривать частицы, соединенные пружинами, мы увидим то же самое явление: от жесткости пружины и происходит термин «жесткое» ОДУ. Даже если мы используем более совершенный численный метод, такой как метод Рунге-Кутта 4-го порядка, это лишь слегка улучшит ситуацию с выбором величины шага, но мы все равно будем иметь серьезные вычислительные проблемы.

Теперь, как мы уже говорили выше, нужно попытаться переформулировать свою задачу так, чтобы избежать появления жесткого ОДУ. Если же это не получится, то нужно использовать неявный метод решения ОДУ. Метод, который мы покажем ниже, является самым простым из неявных методов. Он основан на том, что шаг обычного метода Эйлера выполняется «наоборот».

Видео:Неявные методы решения жестких систем ОДУ и возможность их параллельной реализацииСкачать

3. Решение жесткого ОДУ

Пусть дано дифференциальное уравнение

Формула явного метода Эйлера

продвигает систему вперед на шаг (h) во времени. Для жестких систем, однако, удобнее заменить эту формулу на следующую

То есть, нам нужно вычислить (f) в точке, в которую мы стремимся попасть ( (textbf_) ), а не в исходной ( (textbf_0) ). (Если представить, что время может двигаться в обратном направление, то смысл этого уравнения очевиден. Оно говорит: «если вы находитесь в (textbf_) , и сделаете шаг (-hf (textbf_)) , то попадете в (textbf_0) ». Так что если ваше ДУ представляет собой систему, движущуюся вспять во времени, то этот шаг имеет смысл. Это просто поиск точки (textbf_) такой, что если запустить время вспять, вы в конечном итоге окажетесь в (textbf_0) .) Таким образом, мы ищем точку (textbf_) такую, что (f) , вычисленная в ней и умноженная на (h) , приводит к исходной точке (textbf_0) . К сожалению, найти (textbf_) из уравнения eqref в общем случае невозможно, если только (f) не является линейной функцией.

Чтобы справиться с этим, заменим (f (textbf_)) линейной аппроксимацией, основанной на разложении (f) в ряд Тейлора. Введем обозначение (Deltatextbf=textbf_-textbf_0) . Подставив его в уравнение eqref, получим

Теперь заменим (f(textbf_0 + Deltatextbf)) следующим приближением

(Заметим, что поскольку (f(textbf_0)) является вектором, то производная (f^prime(textbf_0)) является матрицей.) Используя это приближение, мы можем записать (Deltatextbf) как

Разделим обе части последнего соотношения на (h) и перепишем результат в виде

где (I) — единичная матрица.

Разрешая это соотношение относительно (Deltatextbf) , получим

Вычисление (textbf_=textbf_0+Deltatextbf) для неявного метода очевидно требует больших вычислительных затрат, чем при использовании явного метода, так как мы должны решать систему линейных уравнений на каждом шаге. Хотя это может показаться серьезным недостатком (в вычислительном плане), не отчаивайтесь (пока). Для многих классов задач, матрица (f^prime) будет разреженной — например, для «решетки» частиц, соединенных пружинами, (f^prime) будет иметь структуру, которая соответствует связям между частицами. (Обсуждение разреженности и методов решений, применимых в этом случае, см. Baraff и Witkin [1]. Основной материал в Press et al. [2] также будет полезен.) В результате, как правило, можно решить уравнение eqref в линейном времени (т. е. за время, пропорциональное размерности (textbf) ). Выигрыш в таких случаях будет весьма существенным: мы, как правило, можем делать большие шаги по времени без потери устойчивости (т. е. без расхождения, как это происходит для явного метода, если длина шага слишком велика). Время, необходимое для решения каждой линейной системы, таким образом, более чем компенсируется тем, шагов можно зачастую сделать на порядки больше, чем при использовании явных методов. (Конечно, код, необходимый для реализации всего этого, гораздо сложнее, чем в явном случае; как мы уже говорили: переделывайте свои задачи в нежесткие, а если не получается, то платите положенную цену.)

Применим теперь неявный метод для решения уравнения eqref. В нашем случае (f(textbf(t))) равно

Дифференцирование по (textbf) дает

Тогда матрица ((1/h)textbf — f^(textbf_0)) будет равна

Обращая эту матрицу и умножая на (f(textbf_0)) , получим

Какова же предельная длина шага в этом случае? Ответ: нет предела! Если позволить (h) расти до бесконечности, мы получаем следующее

Это означает, что мы достигнем (textbf_=textbf_0 + (-textbf_0)=0) за один шаг! В общем случае для жесткого ОДУ мы не сможем сделать шаг произвольного размера, но мы сможем сделать его гораздо большим, чем если бы использовали явный метод. Дополнительные расходы на решение системы линейных уравнений компенсируются экономией, возникающий благодаря возможности сделать меньше шагов.

Видео:Метод Эйлера. Решение систем ДУСкачать

4. Решение уравнений второго порядка

Большинство задач динамики записывается в виде ДУ 2-го порядка

Это уравнение легко преобразуется систему ДУ 1-го порядка, добавлением новых переменных. Если мы определим (textbf=dot<textbf>) , то сможем переписать уравнение eqref в виде

что представляет собой систему ДУ 1-го порядка. Однако, применяя обратный (неявный) метод Эйлера к уравнению eqref, получим линейную систему размера (2n times 2n) где (n) — размерность (textbf) . Простое преобразование позволяет уменьшить размер линейной системы до (n times n) . Важно отметить, что обе системы — исходная и преобразованная — будут иметь одинаковую степень разреженности. Таким образом, решение системы меньшего размера будет выполняться быстрее.

Система (n times n) , которая должна быть решена, получается следующим образом. Введем для краткости следующие обозначения (textbf_0=textbf(t_0)) и (textbf_0=textbf(t_0)) . Определяем (Deltatextbf) и (Deltatextbf) как (Deltatextbf = textbf(t_0+h)-textbf(t_0)) и (Deltatextbf = textbf(t_0+h)-textbf(t_0)) . Очередное приближение по неявному методу Эйлера, примененному к уравнению eqref, дает в результате

Применяя к (f) разложение в ряд Тейлора, которое в данном контексте является функцией и (textbf) и (textbf) , получим приближение 1-го порядка

В этом уравнении, производная (partial f / partialtextbf) оценивается в точке ((textbf_0, textbf_0)) и аналогично вычисляется (partial f / partialtextbf) . Подставляя это приближение в уравнение eqref, получим линейную систему

Подставив во вторую строку последнего равенства соотношение (Deltatextbf = h(textbf_0 + Deltatextbf)) (т. е. первую строку того же равенства), придем к

Вводя единичную матрицу (I) и перегруппировав члены, получим соотношение

из которого находим (Deltatextbf) . А зная (Deltatextbf) легко вычислить (Deltatextbf = h(textbf_0 + Deltatextbf)) .

Выше, мы предполагали, что функция (f) не зависит явно от времени. Если же (f) зависит от времени явно (например, если (f) описывает изменяющиеся во времени внешние силы), то в уравнение eqref добавляется член, позволяющий учесть эту зависимость

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Ссылки

1. D. Baraff and A. Witkin. Large steps in cloth simulation. Computer Graphics (Proc. SIGGRAPH), 1998.
2. W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling. Numerical Recipes. Cambridge University Press, 1986.

Читайте также

Видео:06 Неявные методы Рунге-КутыСкачать

Комментарии

Дмитрий Храмов
Компьютерное моделирование и все, что с ним связано: сбор данных, их анализ, разработка математических моделей, софт для моделирования, визуализации и оформления публикаций. Ну и за жизнь немного.

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Методы явные и неявные

Дата добавления: 2015-06-12 ; просмотров: 15060 ; Нарушение авторских прав

Процесс формирования математической модели для численного интегрирования обязательно включает этап алгебраизации, который состоит в преобразовании обыкновенных дифференциальных уравнений в алгебраические. Он основан на использовании одного из методов численного интегрирования.

Если задано дифференциальное уравнение

(3.1)

и начальные условия , то очередное значение может быть получено интегрированием (3.1):

(3.2)

Определенный интеграл в (3.2) численно равен площади под кривой на интервале (рис. 3.2).

Приближенно эта площадь может быть вычислена как площадь прямоугольника, высота которого равна значению функции на левой границе интервала или значению на правой границе интервала. Очевидно, площади обоих прямоугольников, ограниченных сверху отрезками 1 и 2 на рис. 3.3, будут тем ближе к точному значению интеграла, чем меньше шаг интегрирования .

Подставив в (3.2) приближенные значения интеграла, можно получить две формулы:

(3.3)

. (3.4)

Выражение (3.3) представляет собой формулу явного метода Эйлера. Называется метод явным потому, что неизвестное значение 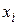может быть непосредственно вычислено по известному значению в предыдущей точке.

Формула (3.4) соответствует неявному методу Эйлера. Здесь в правой части выражения используется неизвестное значение 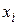, поэтому вычислить его непосредственно по этой формуле нельзя.

Более точное значение интеграла (3.2) дает метод трапеций, которому соответствует отрезок 3 на рис. 3.3. Тогда

. (3.5)

Эта формула относится, очевидно, тоже к неявным.

Для явных методов процедура формирования модели для численного интегрирования ограничивается алгебраизацией исходных дифференциальных уравнений. В частности, формула (3.3) не требует дальнейших преобразований и готова для применения.

Для неявных методов дальнейшие действия зависят от того, какой метод решения системы нелинейных уравнений реализован в данном пакете. Одним из вариантов может быть использование итерационного метода Ньютона, который, как известно, обладает наибольшей скоростью сходимости среди практически применяемых методов, и в котором многократно решается система линеаризованных алгебраических уравнений.

В этом случае реализуется второй этап подготовки математических моделей для неявных методов, который состоит в линеаризации нелинейных алгебраических уравнений, т.е. в разложении нелинейных функций в ряд Тэйлора и сохранении в результате только линейных членов.

Пусть задано нелинейное алгебраическое уравнение

(3.6)

где – вектор переменных.

Разложение (3.6) в ряд Тэйлора с сохранением только линейных членов дает приближенную замену

(3.7)

где –начальное приближение, в качестве которого берутся значения переменных на предыдущем шаге интегрирования;

– неизвестное значение переменной на шаге интегрирования.

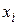
Выражение (3.7) может быть записано как линейное алгебраическое уравнение

,(3.8)

где – вычисляется для известных значений переменных на предыдущем шаге интегрирования;

Таким образом, процесс численного моделирования в общем случае нелинейных систем неявными методами состоит в формировании и решении на каждом шаге интегрирования системы линейных алгебраических уравнений

, (3.9)

которая включает компонентные и топологические уравнения моделируемой схемы. При этом, процедурам алгебраизации и линеаризации подвергаются только компонентные уравнения, так как топологические уравнения всегда линейные алгебраические.

Рассмотрим пример связанный с подготовкой модели для численного решения нелинейного дифференциального уравнения второго порядка

Первым шагом является сведение данного уравнения к задаче Коши, т.е. к системе уравнений первого порядка за счет введения новой переменной :

Явные формулы метода Эйлера имеют вид

Неявные формулы запишутся следующим образом:

Для перехода к матричной записи выполним ряд преобразований:

Здесь ,

Матричная запись имеет вид

.

Формулу (3.7), вообще говоря, необходимо применять итерационно. Решение этого уравнения, найденное для заданного начального приближения , следует использовать в качестве очередного приближения в (3.7) и повторять формирование и решение линейного алгебраического уравнения до тех пор, пока два последовательных приближения не станут близкими с заданной точностью. При численном моделировании можно ограничиться только одной итерацией, выбирая достаточно малый шаг интегрирования и учитывая, что при этом значения переменных на предыдущем шаге являются достаточно хорошим приближением.

3.2.3. Выбор между явными и неявными методами
в процедурах моделирования технических систем

Выбор между явными и неявными методами представляет серьезную проблему. Многие специалисты считают неявные методы более мощным и универсальным инструментом для решения задач моделирования технических систем [23, 15]. Следует, однако, заметить, что лишь недавно появились достаточно мощные и универсальные системы автоматизированного моделирования, такие, как, например, MATLAB или МВТУ [17], допускающие выбор явного или неявного метода решения задачи. Раньше использовались либо явные, либо неявные методы, так как это требовало разных компонентных моделей.

В современных перспективных системах автоматизированного моделирования, пригодных для моделирования технических систем, применяются, как правило, неявные методы численного интегрирования. Неявные методы лучше приспособлены для решения систем дифференциальных и алгебраических уравнений, к тому же они более устойчивы. В результате, несмотря на большие затраты машинного времени на каждом шаге интегрирования, связанные с необходимостью решения СЛАУ, общие затраты могут быть значительно меньше за счет увеличения шага интегрирования и уменьшения общего количества шагов.

Рассмотрим эту особенность неявных методов на примере явного и неявного методов Эйлера [21], определяемых формулами (3.3) и (3.4), соответственно.

Применим указанные формулы для численного интегрирования простейшего линейного дифференциального уравнения

.

Характеристическое уравнение данной динамической системы имеет вид

, или ,

где – постоянная времени системы.

Единственный полюс системы находится в левой полуплоскости, следовательно, исходная система устойчива. Соответственно, любое решение уравнения, при , стремится к нулю.

Разностное уравнение, соответствующее численному решению явным методом Эйлера, запишется как

.

Известно, что условием устойчивости полученного разностного уравнения является

или .

Это означает, что выбор может качественно изменить вид решения, превратив устойчивый процесс в неустойчивый.

Таким образом, на шаг интегрирования наложено очевидное ограничение – он не может быть больше постоянной времени системы, иначе дискретная аппроксимация станет неустойчивой. Если система имеет несколько постоянных времени, то подобное ограничение связывает шаг интегрирования с самой маленькой постоянной времени.

Переход к методам более высокого порядка мало меняет картину. Для метода Рунге – Кутты 4-го порядка требование устойчивости ограничивает шаг величиной , или, в более общем виде, , где – максимальное собственное значение матрицы Якоби [29].

Применение неявного метода Эйлера к той же системе дает

,

где ограничение на величину шага выглядит по-другому:

,

что позволяет выбрать шаг любой величины, ориентируясь только на требуемый уровень погрешности.

Видео:Системы дифференциальных уравнений. Часть 2Скачать

Курсовая работа: Решение систем дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка

Кафедра вычислительной математики и программирования

Пояснительная записка к курсовому проекту

«Решение систем дифференциальных уравнений при

помощи неявной схемы Адамса 3-го порядка»

1. Постановка задачи

2. Описание математических методов решения

3. Описание используемого метода

4. Описание блок-схемы

5. Описание программы

6. Анализ результатов

Бурное развитие в последнее десятилетие информационных технологий и компьютерной техники способствует возникновению всё более сложных математических задач, для решения которых без применения численных методов требуется значительное время. Очень часто перед специалистом возникают задачи, не требующие абсолютно точного решения; как правило, требуется найти приближенное решение с заданной погрешностью. Наряду с совершенствованием компьютерной техники происходит процесс совершенствования и численных методов программирования, позволяющих за минимальный отрезок времени получить решение поставленной задачи с заданной степенью точности.

Одной из таких задач является решение систем дифференциальных уравнений. Обыкновенными дифференциальными уравнениями можно описать поведение материальных точек в силовом поле, законы химической кинетики, уравнения электрических цепей и т. д. Ряд физических задач может быть сведён к решению дифференциальных уравнений или системы дифференциальных уравнений. Задача решения системы дифференциальных уравнений имеет важное прикладное значение при решении научных и технических проблем. Кроме того, она является вспомогательной задачей при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований. Поэтому для инженеров крайне важно грамотно находить решение этой задачи.

1. Постановка задачи

Необходимо решить с заданной степенью точности задачу Коши для системы дифференциальных уравнений на заданном интервале [a,b]. Добиться погрешности на втором конце не более 0,0001. Результат получить в виде таблицы значений приближенного и точного решений в точках заданного интервала. Построить графики полученных решений и сравнить их с точным решением.

– система дифференциальных уравнений вида:

– интервал, на котором ищется решение: [a,b]

– погрешность, с которой ищется решение: е

– формулировка задачи Коши в начальной точке заданного интервала: u(a)=u, v(a)=v

– количество узлов сетки, для которой формируется таблица значений приближенного и точного решений системы: nx

– шаг вывода на экран значений искомых функций в узлах заданной сетки: np

– таблица значений приближенного и точного решений в узлах заданной сетки;

– графики полученных и точных решений.

2. Описание математических методов решения задачи

Конкретная прикладная задача может привести к дифференциальному уравнению любого порядка или к системе таких уравнений. Произвольную систему дифференциальных уравнений любого порядка можно привести к некоторой эквивалентной системе дифференциальных уравнений первого порядка. Среди таких систем выделяют класс систем, разрешённых относительно производной неизвестных функций:

(2.1)

Дифференциальное уравнение или система дифференциальных уравнений имеет бесконечное множество решений. Единственные решения выделяют с помощью дополнительных условий, которым должны удовлетворять искомые решения. В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование и единственность решений.

Первый тип – это задачи Коши, или задачи с начальными условиями. Для таких задач кроме исходного уравнения в некоторой точке a должны быть заданы начальные условия, т.е. значения функции u1(a),…, um(a):

u1(a)=,…, um(a)= (2.2)

Ко второму типу задач относятся так называемые граничные, или краевые задачи, в которых дополнительные условия задаются в виде функциональных соотношений между искомыми решениями. Количество условий должно совпадать с порядком n уравнения или системы. Если решение задачи определяется в интервале xÎ[a,b], то такие условия могут быть заданы как на границах, так и внутри интервала.

Третий тип задач для систем дифференциальных уравнений – это задачи на собственные значения. Такие задачи отличаются тем, что кроме искомых функций u1(x),…, um(x) в уравнения входят дополнительно n неизвестных параметров l₁ , l₂ , . l_n , которые называются собственными значениями. Для единственности решения на интервале [a,b] необходимо задать n + m граничных условий.

Рассмотрим подробнее задачу Коши. Воспользуемся компактной записью задачи (2.1), (2.2) в векторной форме:

(2.3)

Требуется найти на интервале [a,b].

Задачу Коши удобнее всего решать методом сеток. Метод сеток состоит в следующем :

1) Выбираем в области интегрирования упорядоченную систему точек a=x1

#pragma resource «*.dfm»

char *opz(char *); // ф-ия преобразования в обратную польскую запись;

double fpr(char *str,double u, double v,double x); // обратныйходпольской

int p=1,s=1,j=1,o=0; // записи;

__fastcall TForm1::TForm1(TComponent* Owner)

void __fastcall TForm1::N5Click(TObject *Sender)

void __fastcall TForm1::Button3Click(TObject *Sender)

void __fastcall TForm1::N7Click(TObject *Sender)

void __fastcall TForm1::N2Click(TObject *Sender) // очисткаформы

🎥 Видео

Системы дифференциальных уравненийСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Метод ЭйлераСкачать

Математика это не ИсламСкачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Система дифференциальных уравнений. Операционный методСкачать

7.3 Функция устойчивости неявных методов Рунге КуттыСкачать

01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать