Нестационарное температурное поле бесконечной пластины описывается уравнением

НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ.

Общие положения. Описание процесса.

Ранее были рассмотрены условия распространения теплоты при стационарном режиме, когда температурное поле не менялось во времени, оставалось постоянным.

Если же температурное поле меняется во времени, т.е. является функцией времени, то протекающие в таких условия процессы называются нестационарными.

Нестационарные процессы теплопроводности встречаются при охлаждении и нагреве металлических заготовок, прокалывании твердых тел, в производстве стекла, обжига кирпича и т.д.

В качестве примера рассмотрим такой случай. Тело внесено в среду более высокой температурой; сразу же между средой и телом возникает процесс теплообмена, и тело начинает прогреваться. Сначала нагреваются поверхностные слои, но постепенно процесс прогрева распространяется вглубь тела (рис. 1.6.1).

По истечении некоторого времени (теоретически бесконечно большого) температура всех частей тела выравнивается и становится равной температуре окружающей среды, т.е. наступает тепловое равновесие.

На рис. 1.6.1 показан характер кривых, полученных при нагревании однородного твердого тела в среде с постоянной температурой .По мере нагрева температура в каждой точке асимптотически приближа­ется к температуре нагревающей среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела. С увеличением времени прогрева эта разность будет уменьшаться и теоретически через достаточно большой отрезок времени она будет равна нулю.

При нестационарном режиме количество переданной теплоты также непостоянно во времени (рис. 1.6.2). По мере прогрева тела количество воспринимаемой теплоты уменьшается и в пределе становится равным нулю. Площадь, заключенная между осями и кривой, определяет собой полное количество теплоты, переданное за время . Эта теплота аккумулируется телом. Нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества.

Аналогичным образом протекает и процесс охлаждения тела, при этом выделенная теплота передается в окружающую среду.

Скорость теплового процесса при нестационарном режиме определяется значением коэффициента температуропроводности

а , .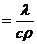

Любой процесс нагревания или охлаждения тела можно разделить на три режима.

Первый режим — начало процесса.

Характерной особенностью этого режима является распространение температурных возмущений в пространстве и захват все новых и новых слоев тела. Скорость изменения температуры в отдельных точках при этом режиме различна и зависит от начальных условий.

Это режим неупорядоченного процесса.

С течением времени скорость изменения температуры во всех точках тела становится постоянной. Это режим упорядоченного процесса, он называется регулярным режимом.

По прошествии длительного времени наступает третий режим, характерной особенностью которого является постоянство распределения температур во времени – это стационарный режим.

Например, в работе паровых котлов нестационарный режим возникает лишь при пуске в работу, выключении и изменении режима работы и имеет временный характер. Поэтому расчет таких аппаратов производится лишь для основного, стационарного режима, а для нестационарного совсем не рассчитывается. В работе же нагревательных печей, наоборот, нестационарный режим является основным, при их расчете приходится определять время, необходимое для прогрева металла до заданной температуры, или температуру, до которой металл нагреется в течение определенного промежутка времени.

Описанный характер изменения температуры и количества переданной теплоты справедливы лишь для твердых тел.

Решение задач нестационарной теплопроводности.

Решить задачу нестационарной теплопроводности это значит найти зависимость изменения температуры и количество теплоты переданной телу во времени для любой точки тела:

Для аналитического нахождения этих зависимостей может быть использовано дифференциальное уравнение теплопроводности Фурье:

.

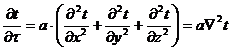
Это уравнение решается с помощью рядов Фурье. Аналитическое решение получается очень сложным и возможно лишь для тел простой формы (пластины, цилиндра и шара) при целом ряде упрощающих предпосылок.

Аналитическое описание процесса теплопроводности кроме дифференциального уравнения также включает в себя и условия однозначности.

Условия однозначности задаются в виде:

· физических параметров , , ;

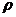
· формы и геометрических размеров объекта ;

· температуры тела в начальный момент времени 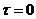; t = t₀ = f(x, у, z).

· граничных условий, которые могут быть заданы в виде граничных условий третьего рода:

.

Дифференциальное уравнение теплопроводности совместно с условиями однозначности дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции, которая удовлетворяла бы уравнению и условиям однозначности.

t=f(x,y,z,i,a,t₀,t_ж, )

Если решить это уравнение для плоской стенки и рассмотреть процесс изменения температуры только в одном направлении x, то решение будет иметь следующий вид:

,

где b иcопределяются из условий стационарности процесса, т.е. при ;

, — из граничных условий 3 рода;

— из начальных условий, т.е. при .

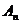
Из уравнения видно, что искомая функция t зависит от большого числа переменных, которые можно сгруппировать в 3 безразмерных комплекса, эти комплексы называются числами подобия.

Первое число подобия — Число Био:

,

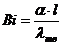
где — коэффициент теплоотдачи на границе жидкости и твердого тела;

λ — коэффициент теплопроводности твердого тела;

l— характеристический размер, который определяется в зависимости от формы тела:

для пластины l=δ;

для цилиндра l= ;

для шара l= .

Второе число подобия — Число Фурье:

,

гдеa— коэффициент температуропроводности;

Число Фурье называют также безразмерным временем.

Третий безразмерный комплекс — безразмерная координата:

.

Установлено, что θ— безразмерная температура, является функцией чисел Био и Фурье, для фиксированных значений , т.е.

.

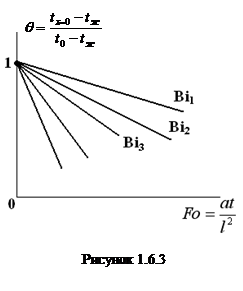
Изменение безразмерной температуры θ для центра ( 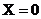) и поверхности ( ) можно представить графическим решением, которое приведено на рисунке 1.6.3.

Подобные графики построены для центра и поверхности пластины, цилиндра и шара, а так же для безразмерного количества теплоты, которая является функцией числа Bi и :

.

Следовательно, чтобы определить температуру на поверхности или в центре тела необходимо знать две величины: число Bi и число .

Таким образом, метод решения задач нестационарной теплопроводности заключается в следующем:

1) задаются геометрическими, начальными и граничными условиями [(с;λ; ; ;α; ),( или )];

2) вычисляют числа Bi и ;

, ;

3) зная числа Bi и по графику, определяют безразмерную температуру θ;

4) определив θ, рассчитывают температуру в центре

или на поверхности тела

,

где — начальная температура тела;

— температура среды.

Рассмотрим влияние значений чисел Bi на распределение температуры в теле на примере охлаждения пластины.

Из полученного решения следует, что для любого момента времени температурное поле имеет вид симметричной кривой с максимумом на оси пластины ( ). В каждый последующий момент будет своя кривая, монотонно убывающая к поверхности (рис. 1.6.4).

Для любого момента времени касательные к кривым в точках проходят через направляющие точки +А и

– А, которые расположены на расстоянии от поверхности пластины, причем

или ,

отсюда , т.е. расстояние до точки А полностью определяется условиями однозначности.

Сказанное справедливо для всех поверхностей.

Видео:Основы теории теплообменаСкачать

Нестационaрные поля температур в многослойной пластине с переменными характеристиками Текст научной статьи по специальности « Математика»

Видео:Температурное поле в плоской пластинке с объемными источниками теплотыСкачать

Аннотация научной статьи по математике, автор научной работы — Осипов Михаил Иванович, Пылаев Анатолий Михайлович

Представлено аналитическое решение задачи расчета нестационарных температурных полей в многоcлойной стенке теплообменного аппарата при условиях третьего рода на граничных поверхностях, первого или второго рода на торцах и при условиях склейки общего вида. Учтена зависимость режимных и теплофизических характеристик от времени и от координат. В решении применена модификация метода Бубнова-Галеркина . В роли базисных функций использованы комбинации полиномов по координатам и тригонометрических функций по времени, удовлетворяющие — с произвольными константами — всем краевым условиям. Приведены примеры расчета распределения температур для теплообменника с винтовой перегородкой и для лопаток высокотемпературных газовых турбин .

Видео:Лекция по теплофизике. 21.10.2021Скачать

Похожие темы научных работ по математике , автор научной работы — Осипов Михаил Иванович, Пылаев Анатолий Михайлович

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Текст научной работы на тему «Нестационaрные поля температур в многослойной пластине с переменными характеристиками»

Николай Константинович Никулин — канд. техн. наук, доцент кафедры «Вакуумная и компрессорная техника» МГТУ им. Н.Э. Баумана. Автор более 100 научных работ в области вакуумной техники.

N.K. Nikulin — Ph. D. (Eng.), assoc. professor of «Vacuum and Compressor Technology» department of the Bauman Moscow State Technical University. Author of more than 100 publications in the field of vacuum technology.

Елена Владимировна Свичкарь — ассистент кафедры «Вакуумная и компрессорная техника» МГТУ им. Н.Э. Баумана. Автор четырех научных работ в области вакуумной техники.

Ye.V. Svichkar — assistant of «Vacuum and Compressor Technology» department of the Bauman Moscow State Technical University. Author of 4 publications in the field of vacuum technology.

УДК 621.184.64; 536.24

М. И. Осипов, А. М. Пылаев

НЕСТАЦИОНAРНЫЕ ПОЛЯ TЕМПЕРАТУР В МНОГОСЛОЙНОЙ ПЛАСТИНЕ С ПЕРЕМЕННЫМИ ХАРАКТЕРИСТИКАМИ

Представлено аналитическое решение задачи расчета нестационарных температурных полей в многослойной стенке теплооб-менного аппарата при условиях третьего рода на граничных поверхностях, первого или второго рода на торцах и при условиях склейки общего вида. Учтена зависимость режимных и теплофи-зических характеристик от времени и от координат. В решении применена модификация метода Бубнова-Галеркина. В роли базисных функций использованы комбинации полиномов по координатам и тригонометрических функций по времени, удовлетворяющие — с произвольными константами — всем краевым условиям. Приведены примеры расчета распределения температур для теплообменника с винтовой перегородкой и для лопаток высокотемпературных газовых турбин.

Ключевые слова: нестационарная теплопроводность, многослойная пластина, модификация метода Бубнова-Галеркина, теплообменник, газовая турбина.

При создании высокоэффективных и надежных теплообменных аппаратов и систем охлаждения газотурбинных установок и теплообменных аппаратов различного назначения ставится задача численного и аналитического исследования внутреннего и нестационарного теплообмена в многослойных стенках корпусных деталей теплообменников и сопловых лопаток. В связи с этим рассмотрим задачу о нестационарных температурных полях (T = T(t, x,y)) в J-слойной пластине

при условиях третьего рода

ag(Tg — T) = (-1)gAdt/dy;

У = ymax = Y g = 2; y = ymin = 0, g = 1 на границах с нормальными координатами, а также при задании тепловых потоков q или температур T при следующих значениях продольных координат:

Q = QCb x = x min = -X/2; Q = (2)

x = x max = X/2; Q G.

В условиях (1) ag — коэффициенты теплоотдачи; Tg — температура среды. В процессе решения учитываем зависимости режимных и те-плофизических характеристик от времени и координат.

При использовании программы для ЭВМ, реализующей численное решение задачи конечно-разностным методом, представляет интерес разработка модификации расчетного метода, не связанного с пошаговой (как по времени, так и по координатам) процедурой и, по-возможности, близкого к аналитическому. Такое решение, в частности, полезно для тестирования численных расчетов.

Основу математической постановки задачи составляет дифференциальное уравнение с кусочно-непрерывными функциями теплопроводности A, объемных теплоемкостей с и тепловыделения W:

cdT = д (AdT ^ + д (AdT ^ + W;

dt dx V dx / dy V dy / ‘ (3)

t > 0, x G (-X/2; X/2), y G (0; Y).

В связи с тем, что функция A не дифференцируема на границах контакта (в точной постановке задачи), вместо уравнения (3) следует рассматривать систему из уравнений теплопроводности, записанных для каждого из слоев в отдельности, при общей односторонней параболической переменной времени [1] :

с 0, x G (-X/2; X/2), y G (yii; yi2).

Однозначное решение задачи (1), (2) и (4) выполнено при дополнительном учете начального распределения температуры:

Тг = Ti^x,y); t = 0, x G [-X/2; X/2], y G [yii;^2], (5) а также при учете для I слоев пластины условий склейки типа

AdTi2 = A дТг+1>1 + P ;

t> 0, Ti2 = Ti+1,1 + Qi; i G .

Слагаемые в уравнении (6), формально соответствующие неидеальности теплового контакта (при = 0) и поверхностному, контактному тепловыделению (при р = 0), включены в целях использования соответствующей программы для ЭВМ при итерационном решении нелинейных задач.

Публикаций по решению рассматриваемой задачи в полной постановке не найдено. Известны лишь результаты анализа для задач в существенно упрощенной постановке, а также общие рекомендации, в частности, по применению обязательно точных методов математической физики для выявления зависимости решения от времени. Применение же, при необходимости, приближенных подходов допустимо лишь по эллиптическим координатам [1]. Судя по публикациям (например, [2]), весьма эффективным представляется метод Бубнова-Галеркина. Применительно к задаче класса (1), (2), (4)-(6) построение решения рекомендовано в виде линейной суперпозиции некоторых функций, называемых базисными и удовлетворяющих граничным условиям. При этом указывается, что коэффициенты разложения следует определять из условий минимизации ортогональной проекции невязки по всей области решения, и подчеркивается, что успех в применении метода определяется выбором структуры и числа базисных функций, входящих в разложение. Но для рассматриваемой задачи конкретных указаний нет.

В нестационарных задачах эти коэффициенты в общем случае представляются функциями времени; поэтому их определению соответствует система линейных дифференциальных уравнений изменения времени. Следует отметить, что в стационарных задачах эти коэффициенты принимаются постоянными и выявляются на основе решений линейных алгебраических систем уравнений, что намного проще. В связи с этим эффективен аналитико-численный подход [1], включающий в себя интегральное преобразование Лапласа, процедуру минимизации невязки для изображения и, наконец, переход к оригиналу. Для определения коэффициентов в разложениях для изображений в данном случае также логично использовать линейные алгебраические уравнения, что и является основным преимуществом названного подхода. К сожалению, в случаях с зависимостью от времени хотя бы немногих параметров (ад, А^, применимость преобразования Лапласа практически исключена.

Сведение трудностей задачи к рассмотрению линейных алгебраических уравнений и без преобразования Лапласа допустимо при использовании в роли совокупности базисных функций систем из произведений тригонометрических функций от времени £ и координат. Такой подход, ранее использованный при решении стационарных задач [3,4], формально применим и при использовании времени в роли аргумента.

Но при этом всегда получаются принципиально бесконечные системы линейных алгебраических уравнений и необходимо обоснование возможности редукции конкретных систем [5], что для рассматриваемой задачи представляется проблематичным.

В настоящей работе опробована модификация метода Бубнова-Галеркина, позволившая ограничиться рассмотрением только систем линейных алгебраических уравнений, применительно к процессам с ограниченной протяженностью во времени £ € [0; £тах = т]. В основном варианте анализа зависимости W = Тн = ,

Я0 = , Ях = считаются кусочно-линейными по нормали к стенке (по у), т.е. линейными по толщине любого слоя. При необходимости учета более сложной зависимости функций от поперечной координаты для каких-либо из физически однородных слоев возможно разбиение каждого из них, например, на ] подслоев с заданием соответствующих подсовокупностей из ] линейных функций. Для характеристики зависимостей температуры Тн от продольной координаты х, тепловых потоков Я0 и Ях от времени , а также искомого решения от х и предусмотрено использование полиномных по х и тригонометрических по времени £ аппроксимаций. Отметим, что применение тригонометрических рядов по времени (при достаточно большом числе слагаемых с заранее неизвестными коэффициентами) в составе каждой из базисных функций обеспечивает принципиально точное решение. Число слагаемых в разложениях для искомых решений ограничено лишь возможностями вычислительных средств, которые позволяют использовать и большое число необходимых уравнений.

Решение Тг, г = 1. I строится в виде суммы трех групп функций: м,и

Тг = Рг+ ^ ^ Нгр Е.р; г = 1. N+М ^ S, (7)

где Нр; р € — функции, последовательно (при £ = 0, х = — Х/2; х = Х/2) удовлетворяющие заданным условиям на границах пространственно-временной области решения; Ер — функции, единичные на соответствующих границах и быстро убывающие до нуля в их окрестностях, например Ер = ехр(—Срр), Ср ^ 1; Рг — функции, удовлетворяющие условиям (1) и (6) и однородным условиям при £ = 0, х = —Х/2; х = Х/2 — функции, удовлетворяющие всем однородным условиям, сответствующим (1), (2), (5), (6). Авторами настоящей работы использована возможность построения функции Р в форме разложений по продольной координате и времени с кусочно-линейными коэффициентами, а именно

Р = Аг + Вг • у, г = 1. I; А = Т + А 1В1/а1, (8)

+ E (^k+i E Pi/Ak+i + Qk))/(AiR); R = E a-1 + E 4/Ak, (9)

4=yk2 — yk2; Ai+i = Аг + (Вг — Bi+i)yi2 — Qi,

Bi+i = (AiBi — Pi)/Ai+i, i = 1. / — 1.

Для базисных функций Gvnm целесообразно применение структуры следующего вида:

Gvnm = Ф(у)(этmt + DvnmcosшД1 — £Vi))^n(x); mt = 2mtn/r; Ф(у) = ,

💥 Видео

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Решение задач теплопроводности (часть 1)Скачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

Решение задач теплопроводности (короткая версия)Скачать

Урок 218. Напряженность электрического поляСкачать

Теплопроводность плоской стенкиСкачать

Подобие процессов конвективного теплообменаСкачать

52. Е.Ю. Просвиряков. Точные решения уравнений гидродинамики для вертикально завихренных теченийСкачать

Учебный фильм - ТеплообменСкачать

Нестационарный теплообмен. часть 1Скачать

6-1. Уравнение теплопроводностиСкачать

Решение уравнения теплопроводности / граничные условия второго и третьего родаСкачать

6-2. Метод сетокСкачать

Вывод уравнения теплопроводностиСкачать

Уравнение теплопроводности в цилиндрических координатахСкачать

Плавление и кристаллизация твердых тел, температура плавления, удельная теплота плавления. 8 класс.Скачать