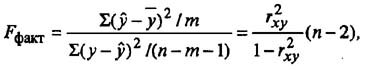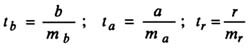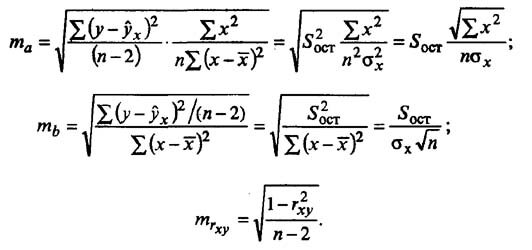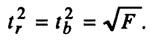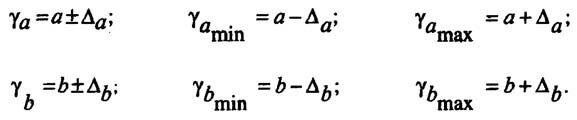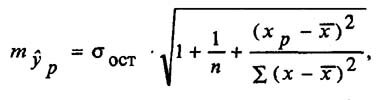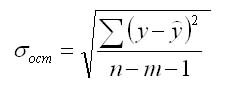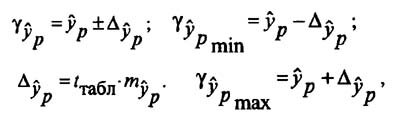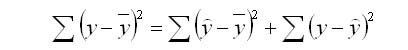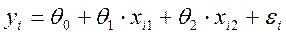Данная задача является модификацией примера регрессионного анализа, рассмотренного в учебнике по экспериментальной психологии Джеймса Гудвина (С. James Goodwin) (2004, с.484, 486-487).
Исследователь пытается выявить взаимосвязь между количеством времени X, бесполезно потраченного студентами, и средним баллом Y их академической успеваемости, который варьируется в пределах от 2,0 до 5,0. Под потраченным без пользы временем понимается количество часов определенного соответствующего времяпровождения в неделю (например, занятого просмотром «мыльных» телесериалов). Данные для выборки студентов приведены в табл. 1
Требуется построить линейную регрессионную зависимость среднего балла успеваемости от показателя бесполезно потраченного времени, а также выполнить прогноз успеваемости для значений X, равных 20, 30 и 40 часов.
В ответе к задаче приведите: а) скорректированный процент объясняемой моделью дисперсии отклика, б) оценку уровня значимости регрессии по F-критерию, в) нестандартизованные коэффициенты регрессионного уравнения и оценки их значимости по t-критерию, г) номер наблюдения, имеющего наибольший по модулю остаток, д) прогнозируемые значения отклика.
Средний балл успеваемости студентов и показатель бесполезно потраченного ими времени
| № | X | Y | № | X | Y | № | X | Y |
| 1 | 2,8 | 4 | 3,9 | 7 | 3,4 | |||
| 2 | 4,0 | 5 | 4,7 | 8 | 4,4 | |||
| 3 | 3,2 | 6 | 4,0 | 9 | 3,80 |
Задачу необходимо при помощи простой регрессионной модели.
Первоначально посмотрим на значение р-уровня значимости по критерию F-Фишера.
| Дисперсионный анализ b | |||||
| Модель | Сумма квадратов | ст.св. | Средний квадрат | Щ | Знч. |
| Регрессия | 2,210 | 2,210 | 27,124 | ,001 a | |
| Остаток | ,570 | ,081 | |||
| Всего | 2,780 | ||||
| a. Предикторы: (конст) время потраченное зря | |||||
| b. Зависимая переменная: успеваемость |
Из таблицы 2 видно, что р-уровень значимости статистически достоверен, поэтому модель может быть содержательно интерпретирована.
Далее посмотрим на значение скорректированного R-квадрата.
| Сводка для модели b | ||||
| Модель | Н | R-квадрат | Скорректи-рованный R-квадрат | Стд. ошибка оценки |
| ,892 a | ,795 | ,766 | ,2854 | |
| a. Предикторы: (конст) время потраченное зря | ||||
| b. Зависимая переменная: успеваемость |
Из таблицы 3 видно, что значение КМД (0,795) достаточно велико, т.е. регрессионная модель объясняет более 79,5% дисперсии зависимой переменной, и результаты предсказания могут быть приняты во внимание, а скорректированный процент объясняемой моделью дисперсии отклика равен 76,6%, что приводит к незначительному уменьшению R-квадрат.
| Коэффициенты a | |||||
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | t | Знч. | |
| B | Стд. Ошибка | Бета | |||
| (Константа) | 5,521 | ,344 | 16,057 | ,000 | |
| Время, потраченное зря | -,060 | ,011 | -,892 | -5,208 | ,001 |
| a. Зависимая переменная: успеваемость |
Из таблицы 4 видно, что значимость регрессионного коэффициента по критерию t-Стьюдента является достоверной (0,001). Вклад переменной (Время, потраченное зря) является значимым — 89%, и мы можем включить данный коэффициент в уравнение.
| № | Время потраченное зря | Успеваемость | Остаток |
| 2,8 | -0,21909 | ||
| 4,0 | -0,15075 | ||
| 3,2 | -0,47426 | ||
| 3,9 | 0,46399 | ||
| 4,7 | 0,13232 | ||
| 4,0 | 0,02793 | ||
| 3,4 | 0,20223 | ||
| 4,4 | 0,01101 | ||
| 3,8 | 0,00662 |
По полученным остаткам, приведенным в базе «Задача 1», видим, что наибольший по модулю остаток имеет испытуемый №3.
У (х)= 5,521 – 0,060*(время потраченное зря).
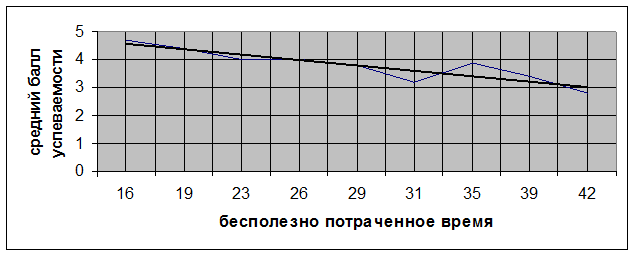
Построим линейную регрессионная зависимость среднего балла успеваемости от показателя бесполезно потраченного времени:
Рис 1. Линейная регрессионная зависимость среднего балла успеваемости от показателя бесполезно потраченного времени.
Прогноз успеваемости для значений X, равных 20, 30 и 40 часов:
У (20) = 5,521 – 0,060 * 20 = 4,321
— студенты, тратящие примерно 20 часов в неделю на бесполезные дела, имеют более высокие оценки зависимой переменной, следовательно, их академическая успеваемость намного выше;
У (30) = 5,521 – 0,060 * 30 = 3,721
— студенты, тратящие без пользы 30 часов в неделю, имеют менее высокие оценки зависимой переменной, соответственно у них наблюдается средняя академическая успеваемость;
У (40) = 5,521 – 0,060 * 40 = 3,121
— учащиеся, которые тратят по 40 часов в неделю без пользы, обладают самыми низкими показателями оценки зависимой переменной и низкой академической успеваемостью.
Таким образом, мы можем сделать вывод о том, что чем большее количество времени тратится студентом на бесполезные дела, тем ниже его академическая успеваемость.
а) скорректированный процент объясняемой моделью дисперсии отклика равен 76,6%;
б) оценка уровня значимости регрессии по F-критерию равна 28, 5;
в) нестандартизованный коэффициент регрессионного уравнения и оценка его значимости по t-критерию равны -0,060 и 0,001 соответственно;
г) наибольший по модулю остаток имеет испытуемый №3;
д) чем большее количество времени тратится студентом на бесполезные дела, тем ниже его академическая успеваемость.
- Технологическая карта дисциплины «Математические методы в психологии» (стр. 7 )
- Критерий Фишера и критерий Стьюдента в эконометрике
- Таблицы по нахождению критерия Фишера и Стьюдента
- Критерии Стьюдента
- Видео лекциий по расчету критериев Фишера и Стьюдента
- Определение доверительных интервалов
- Анализ линейных моделей множественной регрессии
- Страницы работы
- Содержание работы
- 🔍 Видео
Видео:Т-критерий Стьюдента за 12 минут. Биостатистика.Скачать

Технологическая карта дисциплины «Математические методы в психологии» (стр. 7 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |
Выполнить дисперсионный анализ MANOVA. Проанализировать результаты эксперимента.
Задания к отчету 4 по дисциплине ММП
Задача 1 Данная задача является модификацией примера регрессионного анализа, рассмотренного в учебнике по экспериментальной психологии Джеймса Гудвина (С. James Goodwin) (2004, с.484, 486-487).
Исследователь пытается выявить взаимосвязь между количеством времени X, бесполезно потраченного студентами, и средним баллом Y их академической успеваемости, который варьируется в пределах от 2,0 до 5,0. Под потраченным без пользы временем понимается количество часов определенного соответствующего времяпровождения в неделю (например, занятого просмотром «мыльных» телесериалов). Данные для выборки студентов приведены в табл. 1
Требуется построить линейную регрессионную зависимость среднего балла успеваемости от показателя бесполезно потраченного времени, а также выполнить прогноз успеваемости для значений X, равных 20, 30 и 40 часов.
В ответе к задаче приведите: а) скорректированный процент объясняемой моделью дисперсии отклика, б) оценку уровня значимости регрессии по F-критерию, в) нестандартизованные коэффициенты регрессионного уравнения и оценки их значимости по t-критерию, г) номер наблюдения, имеющего наибольший по модулю остаток, д) прогнозируемые значения отклика.
Средний балл успеваемости студентов и показатель бесполезно потраченного ими времени
Задача 2 В консультационной фирме проведено исследование, в ходе которого у группы сотрудников информационно-аналитического отдела в шкале стэнайнов определялись следующие показатели: УПМ — уровень профессиональной мотивации, УКХ — суммарный уровень когнитивных характеристик, ОЭФ — объективный показатель эффективности профессиональной деятельности. Полученные данные приведены в табл. 2
Требуется построить линейную регрессионную зависимость эффективности изучаемой трудовой деятельности от показателей профессиональной мотивации и суммарного уровня когнитивных характеристик. Кроме этого, надо построить графики распределения остатков, в частности — гистограмму и график с нормальной прямой.
В ответе к задаче приведите: а) скорректированное значение коэффициента множественной детерминации, б) оценку уровня значимости регрессии по F-критерию, в) нестандартизованные коэффициенты регрессионного уравнения и оценки их значимости по t—критерию, г) номер наблюдения, имеющего наибольший по модулю остаток.
Показатели профессиональной мотивации, когнитивных характеристик и эффективности труда
Задача 3 В централизованной бухгалтерии, обслуживаю щей сеть подразделений и филиалов коммерческой организации, измерен (в стэнайнах) ряд частных критериев эффективности труда бухгалтеров: Э1 — оценка качества труда специалиста руководителем предприятия, Э2 — количество выполненных хозяйственных операций, ЭЗ — количество ошибок в журнале операций, Э4 — количество нарушений графика сдачи отчетности, Э5 — оценка коллегами качества трудового взаимодействия с данным специалистом, Э6 — количество обработанных первичных документов, Э7 — фактическое рабочее время (на рабочем месте), Э8 — количество кон тактов с внешними контрагентами предприятия, Э9 — субъективная удовлетворенность трудом. Кроме того, с помощью экспертного оценивания для каждого испытуемого определено значение Эинт. интегрального (суммарного) показателя эффективности труда (табл. 3).
Постройте оптимальную линейную регрессионную зависимость интегрального показателя эффективности изучаемого труда от частных показателей, применив в качестве критерия оптимальности наименьшее количество предикторов, обеспечивающее: а) уровень значимости модели по F-критерию Фишера не хуже 0,01, б) объяснение не менее 80% дисперсии отклика, в) значимость коэффициентов регрессионного уравнения не ниже 0,05. Кроме этого, постройте графики распределения остатков, в частности — гистограмму и график с нормальной прямой.
В ответе к задаче приведите: а) скорректированный процент объясняемой дисперсии отклика, б) оценку уровня значимости регрессии, в) нестандартизованные коэффициенты регрессии и оценки их значимости, г) номер наблюдения, имеющего наибольший по модулю остаток.
Показатели эффективности профессиональной деятельности специалистов экономического профиля
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Видео:t-критерий Стьюдента для проверки гипотезы о средней в MS ExcelСкачать
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео:T-критерий или критерий стьюдента. Однофакторная регрессионная модель. Коэффициент корреляцииСкачать

Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Видео:Проверка гипотезы о значимости коэффициентов уравнения регрессииСкачать

Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
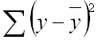
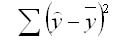
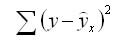
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R 2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Видео:Однофакторная регрессионная модель. Коэффициенты детерминации, корреляции. Критерий ФишераСкачать

Анализ линейных моделей множественной регрессии
Страницы работы
Содержание работы
Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
по лабораторной работе №3
Студентки: Габова Л.А.
Преподаватель: Колесникова А.Ю.
Цель: ознакомиться с основными положениями, понятиями и методами анализа линейных моделей множественной регрессии.
1. Уравнение зависимости веса собранного урожая от количества обобранных кустов винограда и орешника:
где 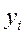
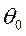
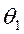
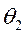
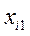
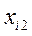
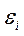
2. С помощью метода наименьших квадратов нашли оценки всех неизвестных параметров уравнения регрессии.
🔍 Видео
Критерий Стьюдента и Фишера в Excel, проверка уравнения множественной регрессии в ExcelСкачать

Коэффициент корреляции. Статистическая значимостьСкачать

Пример проверки гипотезы о незначимости регрессииСкачать

Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Математика #1 | Корреляция и регрессияСкачать

Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Регрессия в ExcelСкачать

Критерий Фишера для проверки адекватности построенной регрессииСкачать

Эконометрика. Линейная парная регрессияСкачать

Стандартизованные коэффициенты регрессииСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Ранговая корреляция СпирменаСкачать