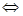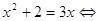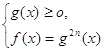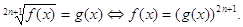Вы умеете решать неравенства? Уверены?
Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.
При решении неравенств мы можем:
1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.
При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.
2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны
3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.
Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.
4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).
5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.
Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.
1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.
Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.
Получаем, что . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.
2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.
Как, например, решить неравенство
Перенесем все в левую часть неравенства, чтобы в правой остался ноль.
Разложим левую часть на множители.
Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: .
Запомним: ответы типа « > » абсурдны.
Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .
4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.
5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.
6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.
7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.
При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.
Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.
А теперь – полезный лайфхак для решения дробно-рациональных неравенств.
Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.
Может быть, сделаем проще? Представим дробь в виде суммы дробей и .
Продолжаем упрощать левую часть:
Теперь можно и привести дроби к одному знаменателю.
Все, больше ничего не пишем. Решаем неравенство методом интервалов.
- Возведение обеих частей уравнения в квадрат
- Квадратные неравенства. Как решать квадратные неравенства?
- Квадратными неравенствами называют неравенства, которые можно привести к виду (ax^2+bx+c) (⋁) (0), где (a),(b) и (с) — любые числа (причем (a≠0)), (x) – неизвестная переменная, а (⋁) – любой из знаков сравнения ((>),( к вадратные уравнения , но со знаком сравнения вместо знака равно. Примеры:
- Как решать квадратные неравенства?
- 💥 Видео
Видео:Когда можно возводить в квадрат неравенства? #shortsСкачать

Возведение обеих частей уравнения в квадрат
2. Возведение обеих частей уравнения в квадрат.
Пусть даны два уравнения 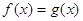
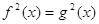
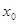
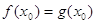
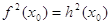
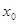
В то же время из равенства квадратов чисел не следует равенство этих чисел (числа могут быть противоположенными). Поэтому из уравнения (2) не следует уравнение (1). Отсюда вытекает, что если при решении уравнения использовалось возведение обеих частей уравнения в квадрат, то нужно повести дополнительное исследование, позволяющее исключить «посторонние» корни, если они появились.
Пример 1. Решить уравнение 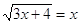
Решение. Возведем обе части этого уравнения в квадрат.
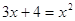
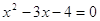
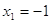
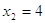
Если 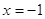
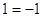
Если 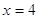
Следовательно, уравнение имеет единственный корень: 4.
3. Выполнение в одной части (или в обеих частях) уравнения тождественных преобразований, приводящих к расширению области определения равнения.
Если некоторое тождественное преобразование привело к расширению области определения уравнения, то получаем уравнения — следствие. При этом могут существовать такие значения переменной, которые являются корнями исходного уравнения.
Пример 1. Решить уравнение 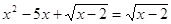
Решение. Выполнив приведение подобных слагаемых, получим: 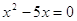
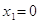
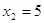
Если 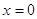
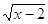
Если 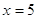
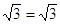
Следовательно, уравнение имеет единственный корень:5.
Пример 2. Решить уравнение 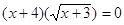
Решение. 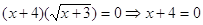
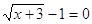
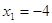
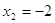
Если 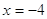
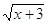
Если 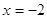
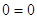
Следовательно, уравнение имеет единственный корень:-2.
Если при решении уравнения мы заменили его уравнением — следствием, то указанная выше проверка является неотъемлемой частью решения уравнения. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в следствие.
Рассмотрим уравнение 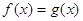
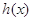
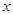
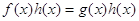
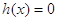
Значит, уравнение (4) есть следствие уравнения (3). Ясно, что уравнения (3) и (4) равносильны, если «постороннее» уравнение 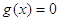
Теорема 1. Если обе части уравнения умножить на 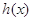
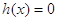
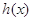
Пример 1. 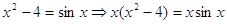
Заметим, что подобное преобразование, т.е. переход от уравнения (4) к уравнению (3) делением обеих частей уравнения (4) на выражение 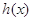
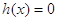
Пример 2. Уравнение 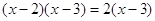
Деление обеих частей уравнения на 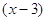
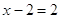
Снова возьмем уравнение (3) и возведем обе его части в квадрат. Получим уравнение: 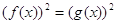
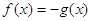
Пример 3. Уравнение 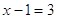
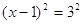
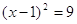
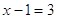
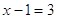
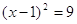
Теорема 2. При возведении обеих частей уравнения в квадрат (и вообще в любую четную степень) получается уравнение, являющееся следствием исходного.
Пример 1. 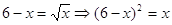
При решении иррационального уравнения чаще всего стараются заменить его более простым, но равносильным исходному. Поэтому важно знать равносильные преобразования.
Определение 10. Уравнение, имеющее одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными. Другими словами два уравнения называют равносильными, если множества их решений совпадают. Равносильность обозначается следующим образом: 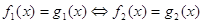
Пример 1. Уравнения 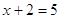
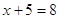
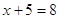
Пример 2. Уравнения 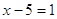
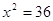
Пример 3. Уравнения 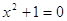
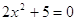
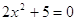
Определение 11. Пусть даны уравнения 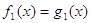
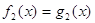
Пример 1. 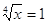
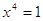
Отметим, что часто множество М совпадает либо с ОДЗ уравнения 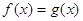
Имеется ряд теорем о равносильности уравнений.
Теорема 3. При возведении обеих частей уравнения в одну и ту же нечетную степень получается уравнение, равносильное исходному.
Пример 1. 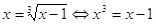
Теорема 4. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное исходному.
Пример 1. 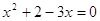
Теорема 5. Если обе части уравнения умножить или разделить на одно и тоже отличное от ноля число, то получится уравнение, равносильное исходному.
Пример 1. 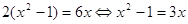
Теорема 6. Если в какой либо части уравнения выполнить тождественные преобразования, не меняющие области определения уравнения, то получится уравнение, равносильное исходному.
В школьной практике при решении иррациональных уравнений чаще всего используются два основных метода:
1) обеих частей уравнения в одну и ту же степень;
2) введение новых (вспомогательных) переменных.
Эти методы будем считать стандартными. В обязательном школьном курсе обычно этими методами и ограничиваются. Однако иногда приходится применять нестандартные методы и искусственные приемы решения иррациональных уравнений.
Типичная ошибка при решении иррациональных уравнений состоит в том, что школьники без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению «посторонних» корней.
При возведении обеих частей иррационального уравнения в одну и ту же степень надо иметь в виду, что если степень — не четное число, то получим равносильное уравнение, если же степень — четное число, то получим уравнение — следствие. Поэтому при решении иррациональных уравнений в большинстве случаев необходима проверка найденных решений.
Проверки можно избежать, если решать иррациональные уравнения с помощью равносильных замен. Для этого полезно знать следующие теоремы.
Теорема 7. Уравнение вида 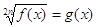
Уравнение вида
Теорема 8. Уравнение вида 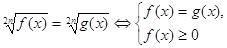
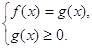
Уравнение вида 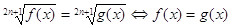
Далее рассмотрим более подробно типы иррациональных уравнений и методы их решения.
Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Квадратные неравенства. Как решать квадратные неравенства?
Квадратными неравенствами называют неравенства, которые можно привести к виду (ax^2+bx+c) (⋁) (0), где (a),(b) и (с) — любые числа (причем (a≠0)), (x) – неизвестная переменная, а (⋁) – любой из знаков сравнения ((>),( к вадратные уравнения , но со знаком сравнения вместо знака равно.
Примеры:
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Как решать квадратные неравенства?
Квадратные неравенства обычно решают методом интервалов . Ниже приведен алгоритм, как решать квадратные неравенства с дискриминантом больше нуля. Решение квадратных неравенств с дискриминантом равным нулю или меньше нуля – разобраны отдельно.
Приведите неравенство к виду (ax^2+bx+c⋁0).
Примеры:
(x^2-6x-16 корни (x_1) и (x_2). Затем запишите исходное выражение в виде (a(x-x_1 ) (x-x_2 )) Подробнее об этом можно почитать здесь .
(x^2-6x-16=0) (-9x^2+x+8=0)
(D=36-4 cdot 1 cdot (-16)=100=10^2) (D=1-4 cdot (-9) cdot 8=289)
(x_1=frac=-2) (x_1=frac=frac=-frac) (x_2=frac=8) (x_2=frac=frac=1)
((x-8)(x+2) )) то точки должны быть выколоты, если неравенство нестрогое (со знаком (≤) или (≥)), то точки должны быть закрашены.

Нанесенные корни разбивают числовую ось на несколько интервалов.
В первом справа интервале поставьте:
(-) знак плюс если перед скобками ничего не стоит или стоит положительное число
(-) знак минус если перед скобками стоит знак минус.
В следующих за ним интервалах поставьте чередующиеся знаки.

Заштрихуйте подходящие интервалы, то есть числовые промежутки :
(-) со знаком «(+)», если в неравенстве стояло «(>0)» или «(≥0)»
(-) со знаком «(-)», если в неравенстве стояло «( )) границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде ((x_1;x_2)) – скобки круглые. При нестрогих знаках неравенства ((≤) или (≥)) — границы интервала ВХОДЯТ в решение, и ответ записывается в виде ([x_1;x_2]), с квадратными скобками на точках.
💥 Видео
Иррациональное уравнение 634. Метод возведения обоих частей уравнения в одну и ту же степень.Скачать

Решение квадратных неравенств | МатематикаСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Возведение неравенства в квадрат | Иррациональные неравенстваСкачать

Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

Возведение иррационального уравнения в квадратСкачать

НЕРАВЕНСТВА возведение в степень 9 класс МакарычевСкачать

НЕРАВЕНСТВА. Контрольная № 1 Алгебра 9 класс.Скачать

Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Как решают уравнения в России и СШАСкачать

Иррациональное неравенство #8Скачать

Опасно возводить в квадрат! Тригонометрия и неравенство. 9, 10, 11 класс.Скачать

Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать