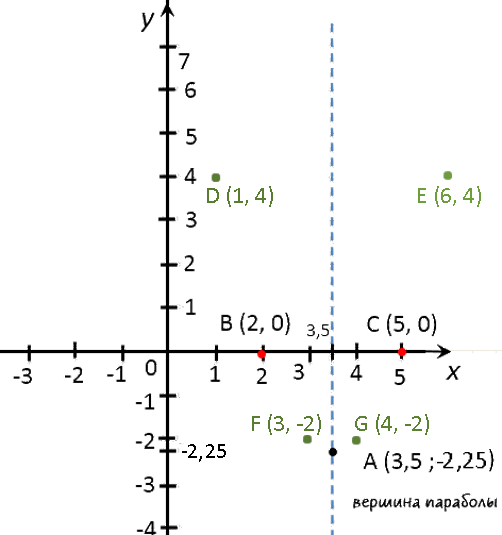- теория по математике 📈 уравнения
- Неполное квадратное уравнение при b=0: ax 2 +c=0
- Неполное квадратное уравнение при с=0: ax 2 +bx=0
- Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0
- Неполные квадратные уравнения
- Основные понятия
- Решение неполных квадратных уравнений
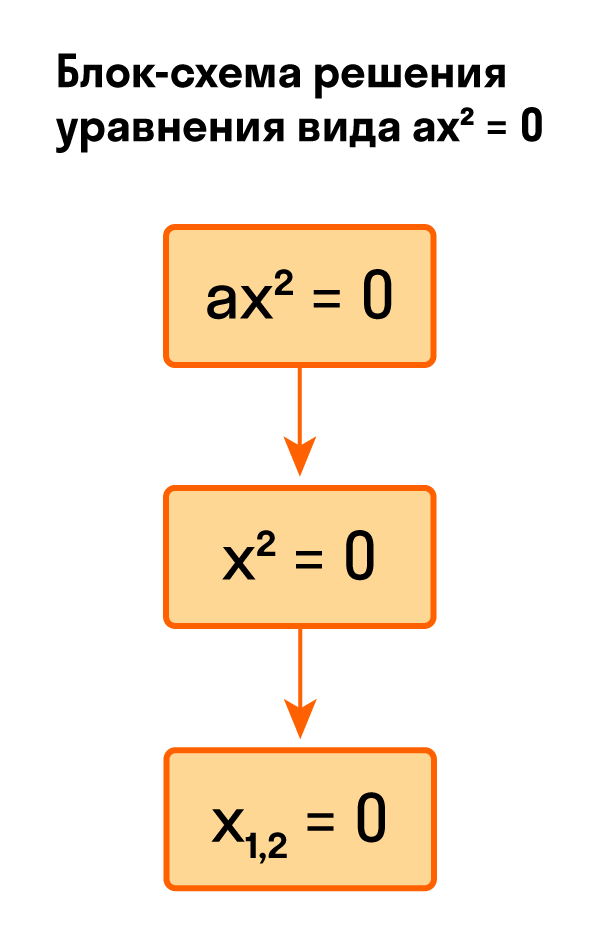
- Как решить уравнение ax² = 0
- Как решить уравнение ax² + с = 0
- В двух словах
- Как решить уравнение ax² + bx = 0
- График функции неполного квадратного уравнения
- Что называют квадратичной функцией
- Как построить график квадратичной функции
- Краткий пример построения параболы
- ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
- ПРАКТИЧЕСКАЯ ЧАСТЬ
- 🎦 Видео
теория по математике 📈 уравнения
Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.
Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.
Неполное квадратное уравнение при b=0: ax 2 +c=0
Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х 2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).
Пример №1. Решить уравнение:
Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х 2 =45; найдем переменную в квадрате, поделив обе части уравнения на 5: х 2 =9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:
Ответ: х=±3 или можно записать ответ так: х1=–3, х2=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:
Выполним решение уже известным способом: –6х 2 =90. х 2 =–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:
Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х1=10, х2=–10.
Неполное квадратное уравнение при с=0: ax 2 +bx=0
Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.
Пример №4. Решить уравнение:
Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.
Пример №5. Решить уравнение:
Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0
Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.
Пример №6. Решить уравнение:
Обе части уравнения делим на (–14) и получаем х 2 =0, откуда соответственно и единственный корень – нуль. Пример №6. Решить уравнение:
Также делим обе части на 23 и получаем х 2 =0. Значит, корень уравнения – нуль.
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Неполные квадратные уравнения
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Квадратное уравнение. 8 класс.Скачать

Основные понятия
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
Неполные квадратные уравнения бывают трех видов:
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Видео:МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать  Решение неполных квадратных уравненийКак мы уже знаем, есть три формулы неполных квадратных уравнений:
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль). Видео:РЕШЕНИЕ НЕПОЛНОГО КВАДРАТНОГО УРАВНЕНИЯ ЗА 5 СЕКУНДСкачать  Как решить уравнение ax² = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0. Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0. Пример 1. Решить −5x² = 0.
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса! Видео:НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ 8 классСкачать  Как решить уравнение ax² + с = 0Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней. В двух словахНеполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
Пример 1. Найти решение уравнения 9x² + 4 = 0.
Разделим обе части на 9: Ответ: уравнение 9x² + 4 = 0 не имеет корней. Пример 2. Решить -x² + 9 = 0.
Разделим обе части на -1: Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3. Видео:Алгебра 8 класс (Урок№27 - Квадратные уравнения. Неполные квадратные уравнения.)Скачать  Как решить уравнение ax² + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника. Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня: Пример 1. Решить уравнение 2x² — 32x = 0
Ответ: х = 0 и х = 16. Пример 2. Решить уравнение 3x² — 12x = 0 Разложить левую часть уравнения на множители и найти корни: Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать  График функции неполного квадратного уравненияПрежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике. Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче. Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать  Что называют квадратичной функциейКвадратичная функция — это функция вида Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит « x » — это « 2 », то перед нами квадратичная функция. Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты « a », « b » и « с ».
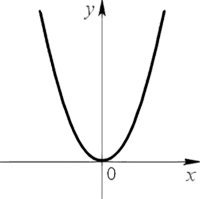
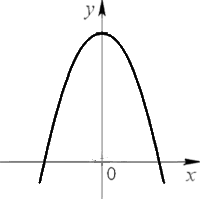
Как построить график квадратичной функцииГрафик квадратичной функции называют параболой. Парабола выглядит следующим образом. Также парабола может быть перевернутой. Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении. Чтобы было проще понять этот алгоритм, сразу разберем его на примере. Построим график квадратичной функции « y = x 2 −7x + 10 ».
Если « a > 0 », то ветви направлены вверх. Если « a », то ветви направлены вниз. В нашей функции « a = 1 », это означает, что ветви параболы направлены вверх. Координаты вершины параболы Чтобы найти « x » (координата вершины по оси « Ox ») нужно использовать формулу:
Найдем « x » для нашей функции « y = x 2 −7x + 10 ».
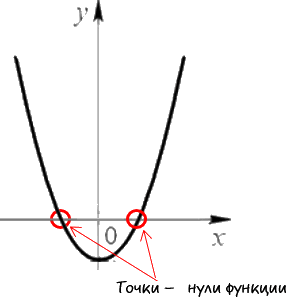
Теперь нам нужно найти « y » (координату вершины по оси « Oy »). Для этого нужно подставить найденное значение « x » в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции». Выпишем полученные координаты вершины параболы. (·) A (3,5; −2,25) — вершина параболы. Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси « Oy ». Для начала давайте разберемся, что называют нулями функции. Нули функции — это точки пересечения графика функции с осью « Ox » (осью абсцисс). Наглядно нули функции на графике выглядят так: Свое название нули функции получили из-за того, что у этих точек координата по оси « Oy » равна нулю. Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции. Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y = 0 ». Подставим в заданную функцию « y = x 2 −7x + 10 » вместо « y = 0 » и решим полученное квадратное уравнение относительно « x » . 0 = x 2 −7x + 10
| x2 = | 7 − 3 | |||||||||||||||||||||||
| 2 | |||||||||||||||||||||||||
| x1 = | |||||||||||||||||||||||||
| 10 | |||||||||||||||||||||||||
| 2 | x2 = | 4 | |||||||||||||||||||||||
| 2 | |||||||||||||||||||||||||
| x1 = 5 | x2 = 2 |
| x | 1 | 3 | 4 | 6 |
| y |
Для каждого выбранного значения « x » рассчитаем « y ».
- y(1) = 1 2 − 7 · 1 + 10 = 1 − 7 + 10 = 4
- y(3) = 3 2 − 7 · 3 + 10 = 9 − 21 + 10 = −2
- y(4) = 4 2 − 7 · 4 + 10 = 16 − 28 + 10 = −2
- y(6) = 6 2 − 7 · 6 + 10 = 36 − 42 + 10 = 4
Запишем полученные результаты в таблицу.
| x | 1 | 3 | 4 | 6 |
| y | 4 | −2 | −2 | 4 |
Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции « y = −3x 2 − 6x − 4 ».
- Направление ветвей параболы « a = −3 » — ветви параболы направлены вниз.

Координаты вершины параболы
| −b |
| 2a |
| −(−6) |
| 2 · (−3) |
| 6 |
| −6 |
y (−1) = (−3) · (−1) 2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
Точки пересечения с осью « Ox » ( y = 0 ).
−3x 2 − 6x − 4 = 0 |·(−1)
| −6 ± √ 6 2 − 4 · 3 · 4 |
| 2 · 1 |
| −6 ± √ 36 − 48 |
| 2 |
| −6 ± √ −12 |
| 2 |
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось « Ox ».
Вспомогательные точки для: « x = −3 »; « x = −2 »; « x = 0 »; « x = 1 ». Подставим в исходную функцию « y = −3x 2 − 6x − 4 ».
- y(−3) = −3 · (−3) 2 − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
- y(−2) = −3 · (−2) 2 − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
- y(0) = −3 · 0 2 − 6 · 0 − 4 = −4
- y(1) = −3 · 1 2 − 6 · 1 − 4 = −3 −6 − 4 = −13
| x | −3 | −2 | 1 | |
| y | −13 | −4 | −4 | −13 |
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки « (−2; −4) » и « (0; −4) ». Построим и подпишем график функции.
Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;
a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x1=2
x2=-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.
График квадратного уравнения вида ax 2 + bx + c или a(x – h) 2 + k представляет собой параболу (U-образную кривую). Для построения графика такого уравнения необходимо найти вершину параболы, ее направление и точки пересечения с осями Х и Y. Если вам дано относительно простое квадратное уравнение, то вы можете подставить в него разные значения «х», найти соответствующие значения «у» и построить график.
🎦 Видео
РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

АЛГЕБРА 8 класс : Решение неполных квадратных уравнений | ВидеоурокСкачать

Как решать неполное квадратное уравнение? 😎Скачать

Неполное квадратное уравнение.Решаем просто.Скачать

Неполное квадратное уравнение.Скачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

7. Неполное квадратное уравнение.Скачать

💂🏻♀️Решение неполного квадратного уравненияСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Реши неполное квадратное уравнение. Математика 8 класс.Скачать