Неотрицательное решение системы линейных уравнений

Системы линейных уравнений

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Содержание

Видео:Неоднородная система линейных уравненийСкачать

Введение

СЛУ можно использовать в экономике для решения экономических задач

Видео:Решение системы уравнений методом ГауссаСкачать

1 Метод нахождения неотрицательного решения СЛУ

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Что такое СЛУ

Система линейных алгебраических уравнений ( линейная система , также употребляются аббревиатуры СЛАУ , СЛУ ) — система уравнений , каждое уравнение в которой является линейным — алгебраическим уравнением первой степени. То есть система m линейных уравнений с n неизвестными ( или , линейная система ) в линейной алгебре — это система уравнений вида

Здесь m — количество уравнений, а n — количество переменных, <displaystyle x_,x_,dots ,x_> — неизвестные, которые надо определить, коэффициенты <displaystyle a_,a_,dots ,a_> и свободные члены <displaystyle b_,b_,dots ,b_> предполагаются известными. Индексы коэффициентов в системах линейных уравнений ( <displaystyle a_> ) формируются по следующему соглашению: первый индекс ( i ) обозначает номер уравнения, второй ( j ) — номер переменной, при которой стоит этот коэффициент.

Система называется , если все её свободные члены равны нулю ( <displaystyle b_=b_=dots b_=0> ), иначе — неоднородной .

Квадратная система линейных уравнений — система, у которой количество уравнений совпадает с числом неизвестных ( m = n ). Система, у которой число неизвестных больше числа уравнений является недоопределённой , такие системы линейных алгебраических уравнений также называются прямоугольными . Если уравнений больше, чем неизвестных, то система является переопределённой .

Система называется совместной , если она имеет хотя бы одно решение, и несовместной , если у неё нет ни одного решения. Решения считаются различными, если хотя бы одно из значений переменных не совпадает.

Система является совместной, так как она имеет, по крайней мере, одно решение ,

Совместная система с единственным решением называется определённой , при наличии более одного решения — неопределённой .

Система называется квадратной , если количество уравнений равно количеству неизвестных.

Равносильными называются две системы уравнений, если они имеют одно и тоже множество решений.

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

СЛУ в алгебре и геометрии

Лине́йная а́лгебра — раздел алгебры , изучающий объекты линейной природы : векторные (или линейные) пространства, линейные отображения , системы линейных уравнений , среди основных инструментов, используемых в линейной алгебре — определители , матрицы , сопряжение . Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры. Такие объекты как квадратичные и билинейные формы, тензоры и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре .

Линейная алгебра обобщена средствами общей алгебры , в частности, современное определение линейного (векторного) пространства опирается исключительно на абстрактные структуры, а многие результаты линейной алгебры обобщены на произвольные модули над кольцом . Более того, методы линейной алгебры широко используются и в других разделах общей алгебры, в частности, нередко применяется такой приём, как сведение абстрактных структур к линейным и изучение их относительно простыми и хорошо проработанными средствами линейной алгебры, так, например, реализуется в теории представлений групп . Функциональный анализ возник как применение методов математического анализа и линейной алгебры к бесконечномерным линейным пространствам, и во многом базируется на методах линейной алгебры и в дальнейших своих обобщениях. Также линейная алгебра нашла широкое применение в многочисленных приложениях (в том числе, в линейном программировании , в эконометрике ) и естественных науках (например, в квантовой механике ).

Слу в геометрии

(3.4)

Каждое уравнение описывает прямую на плоскости; координаты точки пересечения указанных прямых являются решением системы (3.4).

Возможны три случая взаимного расположения двух прямых на плоскости:

1) прямые пересекаются, т.е. коэффициенты системы (3.4) не пропорциональны:

; (3.5)

2) прямые параллельны, т.е. коэффициенты системы (3.4) подчиняются условиям

; (3.6)

3) прямые совпадают, т.е. все коэффициенты пропорциональны

. (3.7)

Запишем определитель системы (3.4)

.

Лишь при выполнении условия (3.5) определитель не равен нулю и система имеет единственное решение (прямые пересекаются в одной точке). В случаях отсутствия решений (прямые параллельны) или при бесконечном множестве решений (прямые совпадают) выполняются соответственно соотношения (3.6) и (3.7), из которых получаем .

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Методы нахождения неотрицательных (опорных) решений СЛУ

Совокупность чисел альфа, взятых в определенном порядке, называют решением слау, если они будучи подставлены в уравнения системы на место соответствующих неизвестных, обращают все уравнения в тождества. Решение называется неотрицательным, если все его компоненты альфа неотрицательны.

Можно считать, что правые части всех уравнений неотрицательны. Последовательно исключая неизвестные, можно привести систему к предпочитаемому виду. Если после этого правые части всех уравнений полученных систем окажутся неотрицательными, то соответствующие базисные решения тоже будут неотрицательными. Следовательно, чтобы получить неотрицательные базисные решения слау, надо сделать так, чтобы свободные члены всех уравнений на всех этапах процесса исключения оставались неотрицательными. Для этого достаточно выбирать разрешающий элемент по определенным правилам. При переходе системы в другую систему используем формулы исключения: ,где r – номер разрешающего уравнения, s – номер разрешающей неизвестной, i не =r. ,i=r. . . А – матрица коэффициентов, В – матрица свободных членов. Так как правые части уравнений должны быть неотрицательны и отбросив случай, когда правые части не изменяются, замечаем, что разрешающий элемент должен быть положительным: ars>0, т.е. в качестве разрешающей можно взять только такую неизвестную, при которой хотя бы в одном уравнении имеется положительный коэффициент. После должно быть выбрано разрешающее уравнение, исходя из условия: >0, откуда следует: . Правила выбора разрешающего элемента. В качестве разрешающей неизвестной можно принять любую неизвестную при которой есть хотя бы один положительный коэффициент, а затем в качестве разрешающего уравнения следует взять то уравнение, которое соответствует наименьшему отношению свободных членов к соответствующим положительным коэффициентам при выбранной неизвестой в этих уравнениях. Если преобразования слау осуществляются методом Жордана-Гаусса с учетом правила выбора разрешающего элемента, то они называются симплексными, т.е. приводящими гарантированно к неотрицательному решению.

Вырожденная слау – система, у которой в каком-либо предпочитаемом виде хотя бы один свободный член = 0, у нее отношение bа может быть одинаково в нескольких уравнениях.

Система не будет иметь ни одного неотрицательного решения, если в процессе симплексных преобразований в ней появится уравнение, в котором свободный член строго положителен, а среди коэффициентов при неизвестных нет ни одного положительного.

Если правые части всех уравнений полученных систем окажутся неотрицательными ,то соответственно базисные решения также будут неотрицательными. =>чтобы получить неотрицательные базисные решения СЛУ ,надо научиться вести процесс исключения неизвестных так, чтобы свободные члены всех уравнений на всех этапах этого процесса оставались неотрицательными. Для этого следует руководствоваться след правилам: 1)если в СЛАУ им отрицательные свободные члены, то все такие уравнения необходимы *(-1); 2)в качестве разрешающей принимать ту переменную, коэффициента при кот хотя бы в одном уравнении системы положителен; 3)для нахождения разрешающего уравнения находят тип отношений столбца свободных членов к положительным элементам разрешающего столбца, в этом сл k-ое уравнение будет разрешающим

Если хотя бы в одном из уравнений системы свободный член положителен, а все коэффициенты при неизвестных

Опорные решения системы линейных уравнений

Применение математических методов в экономике приводит к необходимости отыскания неотрицательных решений системы линейных уравнений, т.е. таких, в которых .

При этом особое значение имеют неотрицательные базисные решения, которые принято называть опорными решениями .

Таким образом, у опорных решений все базисные неизвестные должны иметь только неотрицательные значения.

Отсюда естественным образом получается один из способов отыскания опорных решений системы: из всех базисных решений выбрать одно, несколько или все (сколько требуется по условию задачи) неотрицательные решения (конечно, если они существуют в нужном количестве или вообще существуют).

Отсюда же видно, что число опорных решений системы может быть значительно меньше числа базисных решений, т.е. пытаться предварительно отыскать все базисные решения – не слишком благодарная работа. Еще раз отметим, что в базисном решении системы значения базисных неизвестных равны свободным членам системы, приведенной к единичному базису, и для того, чтобы базисное решение оказалось опорным, необходимо и достаточно, чтобы эти свободные члены были неотрицательными.

Поэтому задачу отыскания опорных решений системы естественно начать с того, чтобы сделать все ее свободные члены неотрицательными (для этого каждое уравнение с отрицательным свободным членом достаточно умножить на (-1)).

Далее можно воспользоваться тем же алгоритмом приведения системы к единичному базису, что и при получении базисных решений, только его следует дополнить специальным правилом выбора ключевого элемента : ключевой столбец (допустим р -й) выбирается так, чтобы он имел хотя бы один положительный элемент , и составляются отношения свободных членов к соответствующим положительным элементам ключевого столбца; то уравнение (пусть q -е), для которого указанное отношение оказывается наименьшим, выбирается в качестве ключевого (ключевой строки).

Таким образом (1)

После получения исходного (первого) опорного решения системы возникает вторая задача, как последовательно перейти от него к следующему, тоже опорному решению. Оказывается, для этого можно использовать алгоритм преобразования однократного замещения, дополненный этим же правилом (1) выбора ключевого элемента.

Преобразования системы с неотрицательными свободными членами к единичному базису, а также преобразования однократного замещения (и те, и другие), при которых выбор ключевого элемента производится по указанному правилу (1), принято называть симплексными преобразованиями .

Для симплексных преобразований справедлива следующая теорема:

Если все свободные члены уравнений системы неотрицательны, то после симплексных преобразований системы они останутся неотрицательными

Сформулированная теорема подтверждает правило отыскания опорного решения методом Жордана-Гаусса, состоящее в соблюдении следующих условий:

1) все свободные члены уравнений системы должны быть неотрицательными; если есть хотя бы один отрицательный свободный член, то соответствующее ему уравнение нужно умножить на (-1);

2) в базис можно ввести только то неизвестное, у которого есть хотя бы один положительный коэффициент;

3) если при неизвестной, вводимой в базис, имеются положительные коэффициенты в нескольких уравнениях, то неизвестная вводится в базис в том уравнении, которому соответствует наименьшее отношение свободных членов к этим положительным коэффициентам.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Примеры задач на нахождение неотрицательных (опорных) решений СЛУ

Пример 1. Найдите опорное решение системы уравнений

Так как во втором уравнении свободный член , умножим это уравнение на (-1). Заполним исходную таблицу Гаусса.

Все свободные члены положительные. При неизвестной есть положительные коэффициенты, значит, можно ее ввести в базис. Поскольку положительные коэффициенты при присутствуют во всех трех уравнениях, следует найти (согласно формуле (1)) минимальное отношение свободных членов к этим положительным коэффициентам, т.е. .

Это минимальное отношение соответствует как первой, так и третьей строке, следовательно, можно вводить в базис как в первом уравнении, так и в третьем. Введем в базис в первом уравнении: ключевой элемент , ключевая строка первая, ключевой столбец первый.

Составляем таблицу Гаусса I итерации.

При неизвестной есть положительные коэффициенты в первом и во втором уравнениях, причем во втором уравнении нет базисной переменной. Но можно ввести в базис только в том случае, если минимальное отношение свободных членов к положительным коэффициентам соответствует второму уравнению.

Находим .

Отсюда следует, что можно ввести в базис во втором уравнении.

Составляем таблицу Гаусса II итерации.

Итак, система приведена к единичному базису. Выпишем общее решение системы

и опорное решение .

Ответ : .

Пример 2. Найдите опорное решение системы уравнений

.

Так как , то в таблицу исходной системы запишем результат умножения первого уравнения на (1).

неизвестную нельзя ввести в базис, не выводя из него , т.к. , что соответствует второму уравнению.

Точно так же нельзя ввести в базис неизвестную , не выводя из него , т.к. приходится на второе уравнение. У неизвестной единственный положительный коэффициент также приходится на второе уравнение. У неизвестной все коэффициенты отрицательные.

Поэтому мы не можем получить опорное решение системы, вводя в базис первой неизвестную . Этот вывод можно было бы сделать быстрее, заметив, что в третьей строке при положительном свободном члене нет ни одного положительного коэффициента при неизвестных.

Попытаемся начать приведение системы к единичному базису с других неизвестных.

Для неизвестной : , поэтому вводим в базис во втором уравнении.

При этом исходная таблица имеет вид:

В третьей строке таблицы I итерации опять нет ни одного положительного коэффициента при неизвестных (при положительном свободном члене). Поэтому мы не можем получить опорные решения, вводя в базис первой неизвестную .

Для неизвестной : , поэтому вводим в базис во втором уравнении. При этом исходная таблица имеет вид:

Таблица I итерации выглядит так:

Теперь ни , ни , ни нельзя ввести в базис, не выводя из него . Остается единственная возможность: ввести в базис в первом уравнении. Получим таблицу II итерации:

Теперь в базис можно ввести лишь неизвестную , но только убрав из него (так как приходится на второе уравнение).

Мы исчерпали все допустимые возможности выбора первой базисной неизвестной (и других) и не смогли получить опорного решения. Следовательно, мы доказали, что данная система опорных решений не имеет.

Ответ : система не имеет опорных решений.

Пример 3 . Найдите опорное решение системы

.

Заполним исходную таблицу Гаусса.

При неизвестной есть два положительных коэффициента и так как , то ввести в базис можно как в первом, так и в третьем уравнении. Введем в базис в первом уравнении.

Получим таблицу I итерации:

Теперь в базис можно вводить неизвестные , , , и только в третьем уравнении ( ). Введем в базис и заполним таблицу II итерации:

Здесь во втором (единственном неиспользованном уравнении) положительный коэффициент только при , но приходится на уже использованное третье уравнение. Поэтому будем пробовать вводить в базис второй неизвестной одну из неизвестных , и (по очереди) и заполнять новые таблицы I и II итерации.Начнем с неизвестной :

Видео:Матричный метод решения систем уравненийСкачать

Примеры решения СЛАУ

Методы решения систем линейных уравнений широко используются в задачах математики, экономики, физики, химии и других науках. На практике, они позволяют не делать лишних действий, а записать систему уравнений в более компактной форме и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять основные методы решения и научиться выбирать оптимальный.

Перед изучением примеров решения задач советуем изучить теоретический материал по СЛАУ, прочитать все теоремы и методы решения. Список тем находится в правом меню.

Примеры по темам:

Видео:Решение систем уравнений методом подстановкиСкачать

СЛАУ: основные понятия, виды

Задание. Проверить, является ли набор $$ решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$

Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$ :

$$3 x-2 y=-6 Rightarrow 3 cdot 0-2 cdot 3=-6 Rightarrow-6=-6$$ $$5 x+y=3 Rightarrow 5 cdot 0+3=3 Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Ответ. Набор $$ является решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$

Задание. Систему $left<begin x-y+z-4 t=0 \ 5 x+y+t=-11 endright.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в матричной форме $A cdot X=B$ , где матрица системы:

$$A=left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)$$

$$A=left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)$$

вектор-столбец свободных коэффициентов:

то есть, запись СЛАУ в матричной форме:

$$left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)left(begin x \ y \ z \ t endright)=left(begin 0 \ -11 endright)$$

Задание. Записать матрицу и расширенную матрицу системы $left<begin 2 x_+x_-x_=4 \ x_-x_=5 endright.$

Решение. Матрица системы $A=left(begin 2 & 1 & -1 \ 1 & -1 & 0 endright)$ , тогда расширенная матрица $tilde=(A mid B)=left(begin 2 & 1 & -1 & 4 \ 1 & -1 & 0 & 5 endright)$

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Критерий совместности системы

Задание. При каких значениях $lambda$ система $left<begin 2 x_-x_+x_+x_=1 \ x_+2 x_-x_+x_=2 \ x_+7 x_-4 x_+2 x_=lambda endright.$ будет совместной?

Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы $tilde$ (слева от вертикальной черты находится матрица системы $A$ ):

и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от второй строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:

Третью строку складываем с первой:

и меняем первую и вторую строки матрицы местами

Видео:Базисные решения систем линейных уравнений (01)Скачать

Квадратные СЛАУ. Матричный метод решения

Теоретический материал по теме — матричный метод решения.

Задание. Найти решение СЛАУ $left<begin5 x_+2 x_=7 \ 2 x_+x_=9endright.$ матричным методом.

Решение. Выпишем матрицу системы $left<begin 5 x_+2 x_=7 \ 2 x_+x_=9 endright.$ и матрицу правых частей $B=left(begin 7 \ 9 endright)$ . Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю: $|A|=1$ ; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что

$$X=left(begin x_ \ x_ endright)=A^ B=left(begin 1 & -2 \ -2 & 5 endright) cdotleft(begin 7 \ 9 endright)=$$ $$=left(begin -11 \ 31 endright) Rightarrowleft(begin x_ \ x_ endright)=left(begin -11 \ 31 endright)$$

Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_=-11$, $x_=31$

Ответ. $x_=-11$, $x_=31$

Задание. Решить с помощью обратной матрицы систему $left<begin 2 x_+x_+x_=2 \ x_-x_=-2 \ 3 x_-x_+2 x_=2 endright.$

Решение. Запишем данную систему в матричной форме:

где $A=left(begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright)$ — матрица системы, $X=left(begin x_ \ x_ \ x_ endright)$ — столбец неизвестных, $B=left(begin 2 \ -2 \ 2 endright)$ — столбец правых частей. Тогда

Найдем обратную матрицу $A^-1$ к матрице $A$ с помощью союзной матрицы:

Определитель матрицы $A$

$$Delta=left|begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright|=2 cdot(-1) cdot 2+1 cdot(-1) cdot 1+1 cdot 0 cdot 3-$$ $$-3 cdot(-1) cdot 1-(-1) cdot 0 cdot 2-1 cdot 1 cdot 2=-4 neq 0$$

Отсюда искомая матрица

Видео:Базисные решения систем линейных уравнений (03)Скачать

Метод / Теорема Крамера

Теоретический материал по теме — метод Крамера.

Задание. Найти решение СЛАУ $left<begin 5 x_+2 x_=7 \ 2 x_+x_=9 endright.$ при помощи метода Крамера.

Решение. Вычисляем определитель матрицы системы:

$$Delta=left|begin 5 & 2 \ 2 & 1 endright|=5 cdot 1-2 cdot 2=1 neq 0$$

Так как $Delta neq 0$ , то по теореме Крамера система совместна и имеет единственное решение. вычислим вспомогательные определители. Определитель $Delta_$ получим из определителя $Delta$ заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:

$$Delta_=left|begin 7 & 2 \ 9 & 1 endright|=7-18=-11$$

Аналогично, определитель $Delta_$ получается из определителя матрицы системы $Delta$ заменой второго столбца столбцом свободных коэффициентов:

$$Delta_=left|begin 5 & 7 \ 2 & 9 endright|=45-14=31$$

Тогда получаем, что

Ответ. $x_=-11$, $x_ = 31$

Задание. При помощи формул Крамера найти решение системы $left<begin 2 x_+x_+x_=2 \ x_-x_=-2 \ 3 x_-x_+2 x_=2 endright.$

Решение. Вычисляем определитель матрицы системы:

$$Delta=left|begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright|=2 cdot(-1) cdot 2+1 cdot(-1) cdot 1+1 cdot 0 cdot 3-$$ $$-3 cdot(-1) cdot 1-(-1) cdot 0 cdot 2-1 cdot 1 cdot 2=-4 neq 0$$

Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:

$$Delta_=left|begin 2 & 1 & 1 \ -2 & -1 & 0 \ 2 & -1 & 2 endright|=2 cdot(-1) cdot 2+(-2) cdot(-1) cdot 1+$$ $$+1 cdot 0 cdot 2-2 cdot(-1) cdot 1-(-1) cdot 0 cdot 2-(-2) cdot 1 cdot 2=4$$ $$Delta_=left|begin 2 & 2 & 1 \ 1 & -2 & 0 \ 3 & 2 & 2 endright|=2 cdot(-2) cdot 2+1 cdot 2 cdot 1+2 cdot 0 cdot 3-$$ $$-3 cdot(-2) cdot 1-2 cdot 0 cdot 2-1 cdot 2 cdot 2=-4$$ $$Delta_=left|begin 2 & 1 & 2 \ 1 & -1 & -2 \ 3 & -1 & 2 endright|=2 cdot(-1) cdot 2+1 cdot(-1) cdot 2+$$ $$+1 cdot(-2) cdot 3-3 cdot(-1) cdot 2-(-1) cdot(-2) cdot 2-1 cdot 1 cdot 2=-12$$

Видео:Решение системы уравнений методом Крамера.Скачать

Метод Гаусса. Метод последовательного исключения неизвестных

Теоретический материал по теме — метод Гаусса.

Задание. Решить СЛАУ $left<begin 2 x_+x_+x_=2 \ x_-x_=-2 \ 3 x_-x_+2 x_=2 endright.$ методом Гаусса.

Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_$ равнялся 1 (это мы делаем для упрощения вычислений):

Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $frac$:

Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

От третьей строки отнимаем вторую, умноженную на 3:

Умножив третью строку на $left(-fracright)$ , получаем:

Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент $$tilde simleft(begin 1 & -1 & 0 & -2 \ 0 & 1 & 0 & 1 \ 0 & 0 & 1 & 3 endright)$$

Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:

Полученной матрице соответствует система

$left<begin x_+0 cdot x_+0 cdot x_=-1 \ 0 cdot x_+x_+0 cdot x_=1 \ 0 cdot x_+0 cdot x_+x_=3 endright.$ или $left<begin x_=-1 \ x_=1 \ x_=3 endright.$

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Однородные СЛАУ. Фундаментальная система решений

Теоретический материал по теме — однородные СЛАУ.

Задание. Выяснить, имеет ли однородная СЛАУ $left<begin 3 x-2 y=-1 \ x+3 y=7 endright.$ ненулевые решения.

Решение. Вычислим определитель матрицы системы:

$$Delta=left|begin 3 & -2 \ 1 & 3 endright|=9-(-2)=9+2=11 neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Задание. Найти общее решение и ФСР однородной системы $Delta=left|begin 3 & -2 \ 1 & 3 endright|=9-(-2)=9+2=11 neq 0$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=left(begin 1 & 1 & 0 & -3 & -1 \ 1 & -2 & 2 & -1 & 0 \ 4 & -2 & 6 & 3 & -4 \ 2 & 4 & -2 & 4 & -7 endright)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & -6 & 6 & 15 & 0 \ 0 & 2 & -2 & 10 & -5 endright)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 9 & -3 \ 0 & 0 & 0 & 12 & -4 endright)$$

От четвертой строки отнимем $$frac$$ третьей и третью строку умножим на $$frac$$ :

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 \ 0 & 0 & 0 & 0 & 0 endright)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 endright)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A simleft(begin 1 & 1 & 0 & -6 & 0 \ 0 & -2 & 2 & 5 & 0 \ 0 & 0 & 0 & 3 & -1 endright)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_, x_$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_,x_,x_$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3-2$ (для проверки, это число должно равняться количеству свободных переменных).

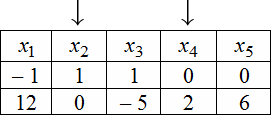
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_=1$ , $x_=0$ получаем, что $left<begin x_=-1+6 cdot 0=-1 \ x_=1-frac cdot 0=1 \ x_=3 cdot 0=0 endright.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_=0$ , $x_=2$, будем иметь, что $x_=12,x_=-5,x_=6$ , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

Общее решение является линейной комбинацией частных решений:

$$X=C_ X_+C_ X_=C_left(begin -1 \ 1 \ 1 \ 0 \ 0 endright)+C_left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

где коэффициенты $C_, C_$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_, C_$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

🔍 Видео

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Решение системы линейных уравнений методом ГауссаСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Графический метод решения систем линейных уравнений 7 классСкачать

Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать