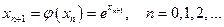- Введение
- Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
- Методы решения систем нелинейных уравнений
- Выбор модельной функции
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
- Метод итераций
- Правила ввода функции
- Достаточные условия сходимости метода итерации
- Итерационные методы решения нелинейных уравнений
- 🎬 Видео
Введение
Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме 
Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

Обозначим через 


Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].
Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.
С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.
Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.
Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.
scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней
method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.
Методы решения систем нелинейных уравнений
Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.
В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

Определим матрицу Якоби:

Запишем(3) в виде:

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

где 

При использовании записи (6) метод Ньютона (5) соответствует выбору:
Система линейных уравнений (5) для нахождения нового приближения 
При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.
Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

Выбор модельной функции
Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:
Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:
Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds
Решение для n=200:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds
Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:
Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds
Вывод: Программа работает и при изменении модельной функции.
Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500
Видео:Решение нелинейного уравнения методом простых итераций (программа)Скачать

Метод итераций
Правила ввода функции
- Примеры
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).
Видео:10 Численные методы решения нелинейных уравненийСкачать

Достаточные условия сходимости метода итерации
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках B2 , B3 .
- Копировать строки итераций до требуемой точности (столбец D ).
Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Итерационные методы решения нелинейных уравнений
Перечислим этапы применения метода итераций для получения корней нелинейных уравнений.
1. Доказать графическим и аналитическим методами существование единственного корня нелинейного уравнения на заданном отрезке.
2. Построить рабочие формулы метода простых итераций, метода Ньютона и модифицированного метода Ньютона, реализующие процесс поиска корня нелинейного уравнения на указанном отрезке.
3. Реализовать построенные итерационные процессы с использованием возможностей Mathcad.
Продемонстрируем выполнение некоторых этапов решения нелинейного уравнения 

1. Воспользуемся графическим методом для отделения корня и докажем его единственность для нелинейного уравнения. Из графика функции 
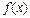



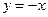
 |
Аналитический метод. Функция 




 |
2. Метод простых итераций. Для построения рабочей формулы перепишем уравнение в виде: 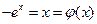

Если условие выполняется, то итерационный процесс строится по формуле
Заметим, что в точке 


Построим функцию 









Итерационный процесс (2) можно начать, задав произвольное начальное приближение 




3. Метод Ньютона. В качестве начального приближения 

Заметим, что в точке 

 |
Следовательно, в качестве начального приближения выбирается точка 

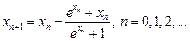
Условия выхода итерационного процесса (4) аналогичны условиям метода простых итераций.
4. Модифицированный метод Ньютона. Начальное приближение 



Условия выхода итерационного процесса (5) аналогичны условиям метода простых итераций.
Замечание: для того, чтобы сделать вывод о скорости сходимости методов, необходимо в каждом методе выбирать одинаковое начальное приближение.
Теоретические вопросы, выносимые на обсуждение
1.Какие команды обеспечивают выполнение символьных операций, которые позволяют упрощать математические выражения, содержащие алгебраические и тригонометрические функции, а также выражения со степенными многочленами.
2.Что означает упрощение.
3.С помощью какой команды можно выполнять символьные вычисления производных и определенных интегралов, заданных соответствующими операторами.
4.Дайте определение производной функции одной переменной.
5.Если речь идет о вычислении численного значения производной, то как оно производится.
6.В чем заключается геометрический смысл производной.
7.Если функции имеют разрывы в точках, то возможно ли определение производных в этих точках, и если да, то какие они.
8.Дайте определение производной второго порядка.
9.Как определяются производные третьего, четвертого и т. д. порядков, словом, производные высшего порядка.
10. Как выполняется взятие производной от функции f(х) в системе Mathcad в символьном виде.
11. Если заданы функции нескольких переменных f(х, у, z . ), то в этом случае о каких производных может идти речь.
12. С помощью каких команд возможно вычисление производных, как первого, так и высшего порядков.
13. В чем заключается геометрический смысл определенного интеграла.
14. Дать определение первообразной функции f(x).
15. Сколько первообразных существует для одной и той же функции f(х).
16. Как из одной интегральной кривой можно получить остальные.
17. С помощью каких команд возможно вычисление значений определенных интегралов приближенным численным методом.
18. Как выполняется взятие неопределенного интеграла в системе Mathcad в символьном виде.
19. С помощью какой команды возможно разложить выражение по степеням простого аргумента.
20. В каком случае команды Symbolics ► Expand и Symbolics ► Simplify являются взаимно обратными.
21. Что происходит при преобразовании выражений командой Expand.
22. С помощью какой команды можно разложить выражение или число на простые множители.
23. Что происходит при применении команды Symbolics ► Factor к полиному.
24. В чем заключается операция факторизации.
25. Как в Mathcad записывается разложение числа на простые множители.
26. В чем заключается операция Symbolics ► Collect.
27. Какая команда используется, если необходимо функцию ряда переменных представить в виде функции заданной переменной, имеющей вид степенного многочлена. Как при этом представлены другие переменные, входящие в заданную функцию.
28. Всегда ли комплектование функции нескольких переменных по базису указанной переменной возможно, и если нет, то, как об этом сообщает система Mathcad.
29. С помощью какой команды можно осуществлять подстановку вместо указанной переменной некоторое другое выражение.
30. Как выполняется подготовка к выполнению операции Symbolics ► Variable ► Substitute.
31. С помощью какой команды можно разложить выражение в ряд Тейлора относительно выделенной переменной с заданным по запросу п числом членов ряда.
32. Запишите ряд Тейлора.
33. В каком случае разложение в ряд называется рядом Маклорена.
34. Запишите ряд Маклорена.
35. Сколько членов по умолчанию выдает команда Symbolics ► Variable ► Expand to Series.
36. Как определить остаточную погрешность.
37. Как можно вычислить определенный интеграл, который не берется в явном виде.
38. Каким численным методом, встроенным в системе Mathcad, вычисляется значение определенного интеграла.
39. Как можно вычислить неопределенный интеграл, который не берется в явном виде.
40. Опишите процедуру взятия неопределенного интеграл с помощью ее разложения в ряд Тейлора и команды Simplify.
41. В чем заключается и когда применяется операция Symbolics ► Variable ► Solve .
42. В чем заключается операция Paste ► Edit.
43. В каком виде записывается результат после действия операции Paste ► Edit.
44. Перечислить этапы исследований в методе итераций для получения корней нелинейных уравнений.
45. Как используется графический метод для выделения корней нелинейного уравнения.
46. Можно ли графическим методом доказать единственность корня на отрезке.
47. Перечислите этапы аналитического метода выделения корней нелинейного уравнения и доказательства его единственности на отрезке.
48. Запишите формулу итерационного процесса.
49. Как определяется начальное значение для итерационного процесса.
50. Когда итерационный процесс завершается.
51. Запишите формулу итерационного процесса в методе Ньютона.
52. Какое достаточное условие должно выполняется, чтобы имела место сходимость метода Ньютона.
53. Как определяется начальное значение для метода Ньютона.
54. В чем заключаются условия выхода из итерационного процесса Ньютона.
55. В чем отличие итерационного процесса Ньютона от модифицированного метода Ньютона.
56. Как произвести сравнительную оценку о скорости сходимости используемых методов.
Задания к вариантам для самостоятельных работ
I Упросить:
1.  | 2.  | 3.  |
4. 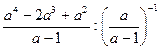 | 5.  | 6. 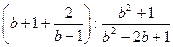 |
7.  | 8.  | 9.  |
10.  | 11.  | 12.  |
13.  | 14.  |
II Разложить подынтегральную функцию в ряд Тейлора и вычислить определенный интеграл. Сравнить полученное значение со значением определенного интеграла вычисленного без использования разложения подынтегральной функции в ряд.
1. 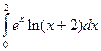 | 2.  | 3.  | 4.  | 5.  |
6.  | 7.  | 8.  | 9.  | 10.  |
11.  | 12.  | 13. 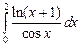 | 14.  . . |
III Найти все корни уравнения, изобразить функцию на координатной плоскости и указать месторасположение корней
1. 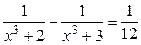 | 2.  | 3.  |
4.  | 5.  | 6.  |
7.  | 8.  | 9.  |
10. 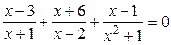 | 11.  | 12.  |
13.  | 14.  |
IV Разложить функцию по простому аргументу х:
| 1. tg5x | 2. sin6x | 3. cos5x | 4. sin8x | 5. ctg7x | 6. ctg4x | 7. tg5x |
| 8. cos7x | 9. sin7x | 10. tg4x | 11. cos9x | 12. tg7x | 13. sin9x | 14.  |
V Вычислить пределы:
1. а).  ; б). ; б).  | 2. а).  ; б). ; б).  . . |
3. а).  ; б). ; б).  | 4. а).  ; б). ; б).  |
5. а).  ; б). ; б).  | 6. а).  ; б). ; б).  |
7. а).  ; б). ; б).  | 8. а).  ; б). ; б).  |
9. а).  ; б). ; б). 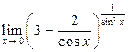 | 10. а).  ; б). ; б).  |
11. а).  ; б). ; б).  | 12. а).  ; б). ; б).  |
13. а).  ; б). ; б).  | 14. а).  ; б). ; б). 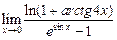 |
VI Вычислить неопределенный интеграл и производную подынтегральной функции
1.  | 2.  | 3.  | 4.  |
5.  | 6.  | 7.  | 8.  |
9. 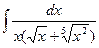 | 10.  | 11.  | 12.  |
13.  | 14.  |
VII Определить количество корней исходного нелинейного уравнения графическим методом. Доказать аналитическим методом единственность корня исходного нелинейного уравнения на указанном отрезке. Построить итерационные формулы, реализующие процесс поиска корня на отрезке методом простых итераций, методом Ньютона и модифицированным методом Ньютона. Провести вычислительный эксперимент и решить уравнение с точностью 

🎬 Видео
Метод Ньютона (метод касательных) Пример РешенияСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

1 3 Решение нелинейных уравнений методом простых итерацийСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Метод половинного деления решение нелинейного уравненияСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Метод простой итерации Пример РешенияСкачать

Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Нелинейные уравнения. Практическая часть. 9 класс.Скачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Метод итерацийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Численные методы решения нелинейного уравнени Теория Шаговый Метод половинного деления Метод НьютонаСкачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать



 ≡ x^2/(1+x)
≡ x^2/(1+x)