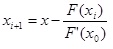Нелинейное уравнение в общем виде (2 видео)

Решение нелинейных уравнений

Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).

Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.

Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.

Рассмотрим несколько методов уточнения корней с определенно заданной точностью.

Содержание

Методы численного решения нелинейных уравнений
Нелинейные уравнения и системы уравнений. Методы их решения.
Нелинейные уравнения и системы уравнений. Методы их решения.
НЕЛИНЕ́ЙНОЕ УРАВНЕ́НИЕ
📽️ Видео

Методы численного решения нелинейных уравнений

Метод половинного деления.

Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b)

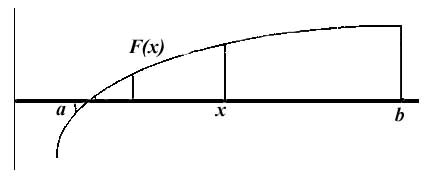
Рис.1. Использование метода половинного деления при решении нелинейных уравнений.

Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.

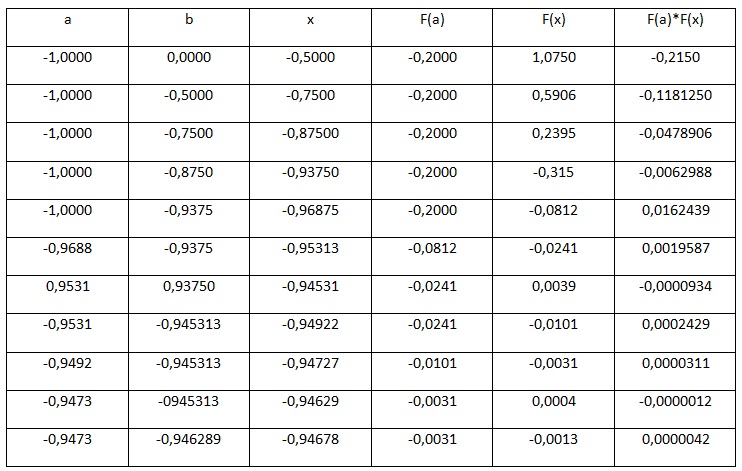
Рис.2. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z)

Рис.3. Использование метода хорд при решении нелинейных уравнений.

Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0;

Определим вторую производную F’’(x) = 6x-0,4.

F’’(-1)=-6,4 0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:

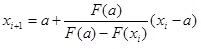
, где x0=b, F(a)=F(-1)=-0,2

Весь произведенный расчет отражен ниже в таблице.

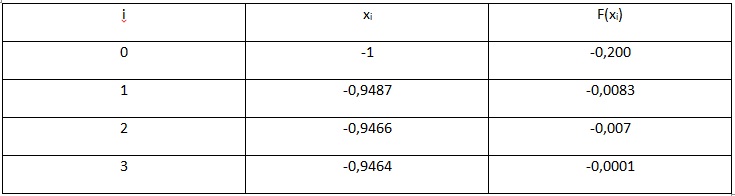
Рис.4. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

Метод касательных (Ньютона)

Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi)

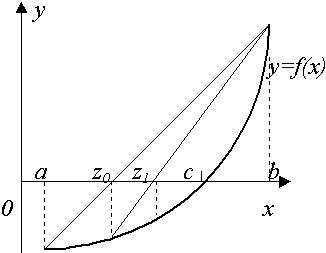
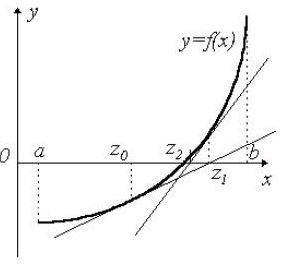
Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.

Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0 выполняется, поэтому расчеты производим по формуле:

Весь произведенный расчет отражен ниже в таблице.

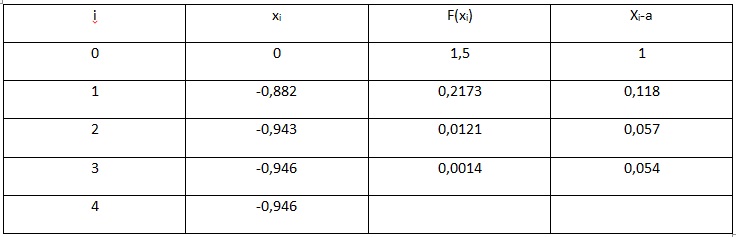
Рис.6. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Видео:Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

Нелинейные уравнения и системы уравнений. Методы их решения.

Видео:Нелинейные уравнения. Практическая часть. 9 класс.Скачать

Нелинейные уравнения и системы уравнений. Методы их решения.

Одной из важных задач прикладной математики является задача решения нелинейных уравнений, встречающихся в разных областях научных исследований.

Под нелинейными уравнениями ( nonlinear equations ) понимаются алгебраические и трансцендентные уравнения с одним неизвестным в следующем виде:

где — действительное число, — нелинейная функция.

Под системой нелинейных уравнений понимается система алгебраических и трансцендентных уравнений в следующем виде:

где < > — действительные числа, < … > — нелинейные функции.

Алгебраическое уравнение — это уравнение содержащие только алгебраические функции, которое можно представить многочленом n ‐ ой степени с действительными коэффициентами (целые, рациональные, иррациональные) в следующем виде:

Трансцендентное уравнение – это уравнение содержащие в своем составе функции, которые являются не алгебраическими. Простейшими примерами таких функций служат показательная функция, тригонометрическая функция, логарифмическая функция и т.д.

Решением нелинейного уравнения (или системы нелинейных уравнений) называют совокупность (группа) чисел , которые, будучи подставлены на место неизвестных , обращают каждое уравнение (или систему уравнений) в тождество:

Для решения нелинейных уравнений (или систем нелинейных уравнений) существует несколько методов решения: графические, аналитические и численные методы.

Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений.

Аналитические методы (или прямые методы) позволяют определить точные значения решения уравнений. Данный метод позволяет записать корни в виде некоторого соотношения (формул). Подобные методы развиты для решения простейших тригонометрических, логарифмических, показательных, а также алгебраических уравнений. Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. В таких случаях обращаются к численным методам, позволяющим получить приближенное значение корня с любой заданной точностью .

Численные методы решения нелинейных уравнений – это итерационный процесс расчета, который состоит в последовательном уточнении начального приближения значений корней уравнения (системы уравнений). При численном подходе задача о решении нелинейных уравнений разбивается на два этапа:

— локализация (отделение) корней

› Под локализацией корней понимается процесс отыскания приближенного значения корня или нахождение таких отрезков, в пределах которых содержится единственное решение

› Под уточнением корней понимается процесс вычисления приближенных значений корней с заданной точностью по любому численному методу решения нелинейных уравнений.

Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно. В случае повторения итерационного процесса при изменении стартовых точек отсутствуют гарантии, что найдется новый корень уравнения, так как итерационный процесс может сойтись к найденному корню.

Для поиска других корней используется метод удаления корней. Данный метод основан на принципе создания новой функции путем деление основной функции на найденный корень уравнения:

Так, например, если — корень функции то, чтобы произвести удаление найденного корня и поиск оставшихся корней исходной функции необходимо создать функцию . Точка будет являться корнем функции на единицу меньшей кратности, чем , при этом все остальные корни у функций и совпадают с учетом кратности. Повторяя указанную процедуру, можно найти все корни с учетом кратности.

Следует обратить внимание, что когда производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз. Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.

Локализация корней.

› Локализация корней аналитическим способом

Для отделения корней уравнения необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция непрерывна на отрезке , а на концах отрезка её значения имеют разные знаки , то на этом отрезке расположен, по крайней мере, один корень. Дополнительным условием, обеспечивающем единственность корня на отрезке является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства первой производной . Таким образом, если на отрезке функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень.

› Локализация корней табличным способом

Допустим, что все интересующие нас корни уравнения находятся на отрезке . Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи. Будем вычислять значения , начиная с точки , двигаясь вправо с некоторым шагом h . Как только обнаруживается пара соседних значений , имеющих разные знаки, так соответствующие значения аргумента x можно считать границами отрезка, содержащего корень.

Надежность рассмотренного подхода к отделению корней уравнений зависит как от характера функции , так и от выбранной величины шага h. Действительно, если при достаточно малом значении h ( ) на границах текущего отрезка функция принимает значения одного знака, то естественно ожидать, что уравнение корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции на отрезке могут оказаться корни уравнения (рис. 1, а). Также несколько корней на отрезке могут оказаться и при выполнении условия (рис. 1, б). Предвидя подобные ситуации, следует выбирать достаточно малые значения h .

Рис. 1. Варианты поведения функции на интервале локализации корня

Поскольку данный способ предполагает выполнение лишь элементарных арифметических и логических операций, количество которых может быть велико при малых значениях h , для его реализации целесообразно использовать вычислительные возможности компьютера.

Отделяя, таким образом, корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска ( h /2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.

Уточнение корней.

На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку , с заданной точностью (погрешностью) e . Это означает, что вычисленное значение корня должно отличаться от точного не более чем на величину e :

Существует большое количество численных методов решения нелинейных уравнений для уточнения корней, которые условно можно разделить:

› Методы решение уравнений с одним неизвестным. Основными представителями являются:

— метод половинного деления;

— метод простой итерации;

— метод Ньютона для уравнения с одним неизвестным;

Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

НЕЛИНЕ́ЙНОЕ УРАВНЕ́НИЕ

В книжной версии

Том 22. Москва, 2013, стр. 345-346

Скопировать библиографическую ссылку:

НЕЛИНЕ́ЙНОЕ УРАВНЕ́НИЕ, алгебраическое или трансцендентное уравнение вида $$f(x)=0,tag1$$ где $x$ – действительное число, $f(x)$ – нелинейная функция. Системой Н. у. называется система $$beginf_1(x_1, x_2. x_n)=0,\ f_2(x_1, x_2. x_n)=0,\ . \ f_n(x_1, x_2. x_n)=0,endtag2$$ не являющаяся системой линейных алгебраич. уравнений. Уравнение (1) и система (2) могут трактоваться как нелинейное операторное уравнение $$L (u)=gtag3$$ с нелинейным оператором $L$ , действующим из конечномерного векторного пространства $R^n$ в $R^n$ .