Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Видео:Эконометрика. Линейная парная регрессияСкачать

Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Видео:Парная регрессия: линейная зависимостьСкачать

Парная нелинейная регрессия
Общий вид регрессионной модели:

Если в уравнении (1) присутствует только один фактор X, а f – нелинейная математическая функция, получим парную нелинейную модель регрессии вида
Различают два класса нелинейных регрессий:
1) регрессии, нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам;
2) регрессии, нелинейные как относительно объясняющих переменных, так и относительно оцениваемых параметров.
К первому классу относятся, например:
1) полиномы разных степеней
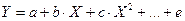
2) равносторонняя гипербола

Ко второму классу относятся:
1) степенная функция



Замечание.
Если модель второго класса с помощью соответствующих преобразований может быть приведена к линейному виду, то она называется внутренне линейной, если же модель не может быть сведена к линейной функции, то она называется внутренне нелинейной (например, 
Работа с такими моделями сводится к их предварительной линеаризации (приведению к линейному виду). Модели их первого класса приводятся к линейному виду простой заменой переменных. Для линеаризации моделей второго класса используют полулогарифмическую функцию или логарифмирование. Полученные таким образом вспомогательные линейные модели оценивают обычным МНК. Затем осуществляют обратный переход к нелинейной функции.
Пример.
Пусть зависимая переменная y – прибыль в семи различных торговых точках (исходные данные приведены в таблице 1), а фактор x – товарооборот в них.
Требуется: см. пункты 8, 9 в методичке.
Степенная модель



обозначим lg y=Y, lg x= X, и получим вспомогательную линейную модель вида
Для ее построения воспользуемся таблицей 1 (столбцы X=lg x и Y=lg y) и результатами регрессионного анализа.
| n | y | x | lg y=Y | lg x=X | yp | ei | ei^2 | eiотн | y-ycp | (y-ycp)^2 |
| 0.301 | 1.699 | 2.464 | -0.464 | 0.215 | 23.200 | -14.286 | 204.082 | |||
| 0.602 | 1.778 | 4.097 | -0.097 | 0.009 | 2.427 | -12.286 | 150.939 | |||
| 1.041 | 1.929 | 10.823 | 0.177 | 0.031 | 1.606 | -5.286 | 27.939 | |||
| 1.230 | 1.929 | 10.823 | 6.177 | 38.151 | 36.333 | 0.714 | 0.510 | |||
| 1.255 | 2.000 | 17.030 | 0.970 | 0.941 | 5.389 | 1.714 | 2.939 | |||
| 1.447 | 2.079 | 28.317 | -0.317 | 0.101 | 1.133 | 11.714 | 137.224 | |||
| 1.531 | 2.146 | 43.527 | -9.527 | 90.773 | 28.022 | 17.714 | 313.796 | |||
| Сумма | 130.222 | 98.110 | 837.429 | |||||||
| Среднее | 16.286 | 91.429 | 14.016 |
Вспомогательная линейная модель примет вид
Обратный переход к степенной функции:
Степенная модель парной регрессии примет вид:

С помощью этой модели рассчитываем все последующие столбцы таблицы 1, начиная с 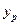
Качественные характеристики модели:

84.4 % случайной вариации переменной прибыль (y) учтено в построенной модели и обусловлено случайными колебаниями фактора оборот (х);

фактические значения прибыли отличаются от рассчитанных на основе степенной модели в среднем на 14 %;
эластичность при степенной связи переменных 


при изменении оборота на 1 % прибыль меняется в ту же сторону на 2,789%, изменение эластично.
|  |
Показательная модель

| n | y | x | lg y=Y | yp | ei | ei^2 | eiотн |
| 0.301 | 3.119 | -1.119 | 1.252 | 55.954 | |||
| 0.602 | 4.245 | -0.245 | 0.060 | 6.125 | |||
| 1.041 | 9.173 | 1.827 | 3.339 | 16.611 | |||
| 1.230 | 9.173 | 7.827 | 61.265 | 46.042 | |||
| 1.255 | 14.564 | 3.436 | 11.807 | 19.089 | |||
| 1.447 | 26.976 | 1.024 | 1.048 | 3.657 | |||
| 1.531 | 49.967 | -15.967 | 254.929 | 46.960 | |||
| Сумма | 333.700 | 194.439 | |||||
| Среднее | 16.286 | 91.429 | 27.777 |
Y=-0.161+0.0133*x – вспомогательная линейная модель.
Окончательно показательная модель примет вид:

Качественные характеристики модели:
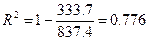
77,6 % случайной вариации переменной прибыль (y) учтено в построенной модели и обусловлено случайными колебаниями фактора оборот (х);

фактические значения прибыли отличаются от рассчитанных на основе модели в среднем на 28 %, модель неточная;
эластичность при показательной связи переменных 


при изменении оборота на 1 % прибыль меняется в ту же сторону на 2,82%, изменение эластично.
|  |
Гиперболическая модель
используем простую замену 

| n | y | x | 1/x=X | yp | ei | ei^2 | eiотн |
| 0.02 | -2.298 | 4.2983 | 18.475 | 214.9137 | |||
| 0.0167 | 5.6834 | -1.683 | 2.8338 | 42.08507 | |||
| 0.0118 | 17.421 | -6.421 | 41.231 | 58.37421 | |||
| 0.0118 | 17.421 | -0.421 | 0.1774 | 2.477429 | |||
| 0.01 | 21.647 | -3.647 | 13.299 | 20.25976 | |||
| 0.0083 | 25.638 | 2.3624 | 5.581 | 8.437161 | |||
| 0.0071 | 28.488 | 5.5118 | 30.38 | 16.21119 | |||
| Сумма | 111.98 | 362.7585 | |||||
| Среднее | 16.286 | 91.429 | 51.82265 |


Качественные характеристики модели:
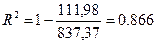
86,6 % случайной вариации переменной прибыль (y) учтено в построенной модели и обусловлено случайными колебаниями фактора оборот (х);

фактические значения прибыли отличаются от рассчитанных на основе модели в среднем на 51,8 %, модель неточная;
эластичность при гиперболической связи переменных 


при изменении оборота на 1 % прибыль меняется в ту же сторону на 1,6%, изменение эластично.
Видео:Парная нелинейная регрессияСкачать

Регрессия: понятие, виды и уравнение
Содержание статьи:
- Уравнение регрессии
- Линейное уравнение
- Нелинейное уравнение
- Виды регрессии
- Парная регрессия
- Множественная регрессия
Регрессия. Многие из нас слышали это слово, но немногие знают, что же это такое на самом деле. Попробуем разобраться. Регрессия — это зависимость между определёнными переменными, с помощью которой можно спрогнозировать будущее поведение данных переменных. Причём, под переменными подразумеваются всевозможные периодические явления вплоть до человеческого поведения.
Видео:Эконометрика. Нелинейная регрессия. Гипербола.Скачать

Уравнение регрессии
Зачастую, регрессия подаётся в виде простого уравнения, которое раскрывает зависимость и силу связи между двумя группами числовых переменных, одна из которых называется зависимой (эндогенной), а вторая — независимой (экзогенной или фактором). Если есть группа взаимосвязанных показателей, то зависимая переменная выбирается логическими размышлениями, а остальные выступают независимыми. То есть, если у нас есть расстояние между городами и затраты на путешествие, то вполне ясно, что затраты будут зависеть от расстояния. Уравнения бывают двух видов: линейные и нелинейные (это уже чистая математика). Стоит рассмотреть каждый из видов.
Видео:Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Линейное уравнение
Линейное уравнение иллюстрирует строго линейную связь между переменными, то есть в нём отсутствуют степени, дроби, тригонометрические функции. Решается стандартными математическими способами.
Видео:Нелинейная регрессияСкачать

Нелинейное уравнение
Логично предположить, что в нелинейный класс уравнений входит всё то, что не вошло в линейный. Решаются такие уравнения сведением к линейному типу, а дальше – по накатанной дорожке.
Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Виды регрессии
Регрессия бывает двух видов: парная (линейная и нелинейная) и множественная (линейная и нелинейная). Разница между ними в виде уравнения и количестве независимых переменных. Логично, что парная регрессия — это когда одна зависимая переменная и одна независимая, в множественной — независимых переменных несколько. В природе имеет место исключительно множественная регрессия, так как нельзя ограничить внешнее влияние на какое-то явление строго одним фактором. Рассмотрим оба вида регрессий детальнее.
Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Парная регрессия
Парная (её ещё называют двухфакторной) модель проста в использовании, так как у нас всего две переменные: эндогенная и экзогенная, а значит будет просто решить уравнение и провести анализ. А это значит, что и применять на практике такую модель очень легко.
Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Множественная регрессия
Множественная (многофакторная) модель намного сложнее, так как мы имеем уравнение с большим количеством переменных, для решения которого существуют определённые математические способы (метод наименьших квадратов например).
Итоги
Немного разобравшись в этой теме, приходишь к выводу, что регрессия очень необходимое понятие, помогающее предугадать поведение многих явлений. Его используют в экономике, психологии, химии, биологии, метеорологии и во многих других науках, причём существует множество программ, которые проводят все необходимые расчёты автоматически и сами выводят результаты и графики для анализа. Пользователю остаётся только считать результаты и правильно расшифровать их. А уж найти им применение вообще не проблема. Поэтому, я считаю, что необходимо иметь хотя бы малейшее понятие о том, что же такое эта пресловутая регрессия и где её использовать.
Видео про линейную регрессию и корреляцию:
🎦 Видео
Эконометрика. Нелинейная регрессия: парабола.Скачать

Эконометрика. Нелинейная регрессия. Полулогарифмические функции.Скачать

Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

нелинейная регрессияСкачать

Парная регрессия: гиперболическая зависимостьСкачать

Математика #1 | Корреляция и регрессияСкачать

Парная регрессия: степенная зависимостьСкачать

1.1 Нелинейная регрессия в ExcelСкачать











