Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
- Виды нелинейной регрессии
- Уравнение регрессии. Уравнение множественной регрессии
- Определение понятия регрессии
- Какие бывают типы связей между переменными
- Виды регрессий
- Гиперболическая, линейная и логарифмическая
- Множественная и нелинейная
- Обратные и парные виды регрессий
- Понятие корреляции
- Методы
- Корреляция для множественной регрессии
- Метод наименьших квадратов
- Параметры уравнений
- Сгруппированные данные
- Множественное парное уравнение регрессии: оценка важности связи
- Какие факторы необходимо учитывать при построении множественной регрессии
- Методы построения
- Методы многомерного анализа
- Лекция 5. Тема Нелинейная регрессия
- Тема 3. Нелинейная регрессия
Видео:Парная нелинейная регрессияСкачать

Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Видео:Эконометрика. Нелинейная регрессия: парабола.Скачать

Уравнение регрессии. Уравнение множественной регрессии
Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.
Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Определение понятия регрессии
В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).
Видео:Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Какие бывают типы связей между переменными
В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.
Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.
Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Виды регрессий
На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.
Видео:Парная регрессия: линейная зависимостьСкачать

Гиперболическая, линейная и логарифмическая
Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.
Видео:Математика #1 | Корреляция и регрессияСкачать

Множественная и нелинейная
Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х1 , х2 . хс)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.
Видео:Эконометрика. Нелинейная регрессия. Полулогарифмические функции.Скачать

Обратные и парные виды регрессий
Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.
Видео:Эконометрика. Нелинейная регрессия. Гипербола.Скачать

Понятие корреляции
Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.
Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Методы
Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.
Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.
В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.
Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).
Видео:нелинейная регрессияСкачать

Корреляция для множественной регрессии
Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.
Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.
Видео:Нелинейная регрессияСкачать

Метод наименьших квадратов
Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.
Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.
Видео:1.1 Нелинейная регрессия в ExcelСкачать

Параметры уравнений
Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.
Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.
Видео:Линейная регрессияСкачать

Сгруппированные данные
Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.
Видео:Решение задачи регрессии | Глубокое обучение на PythonСкачать

Множественное парное уравнение регрессии: оценка важности связи
Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x1,x2,…,xm)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.
Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.
Линейная функция изображается в форме такой взаимосвязи: у = а0 + a1х1 + а2х2,+ . + amxm. При этом а2, am, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.
Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах1 b1 х2 b2 . xm bm . В данном случае показатели b1, b2. bm – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.
Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Какие факторы необходимо учитывать при построении множественной регрессии
Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.
Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:
- Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
- Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
- В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.
Видео:007. Нелинейная регрессия - К.В. ВоронцовСкачать

Методы построения
Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:
- Способ исключения.
- Способ включения.
- Пошаговый анализ регрессии.
Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.
Видео:Множественная регрессия в ExcelСкачать

Методы многомерного анализа
Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.
Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Лекция 5. Тема Нелинейная регрессия
| Название | Тема Нелинейная регрессия |
| Дата | 16.02.2021 |
| Размер | 200.5 Kb. |
| Формат файла |  |
| Имя файла | Лекция 5.doc |
| Тип | Документы #176688 |
 С этим файлом связано 4 файл(ов). Среди них: Bukhgaltersky_upravlenchesky_uchyot_shpory.doc, 580_taym-menedzhment.doc, vnutrennyaya_politika_aleksandra_i.doc, ККЛ Страховой бизнес_Пожидаева.doc. С этим файлом связано 4 файл(ов). Среди них: Bukhgaltersky_upravlenchesky_uchyot_shpory.doc, 580_taym-menedzhment.doc, vnutrennyaya_politika_aleksandra_i.doc, ККЛ Страховой бизнес_Пожидаева.doc.  Показать все связанные файлы Подборка по базе: 10 тема тесты.docx, План конспект урока по Истории Средних веков тема урока_ _Кресто, 8. Гр. 7. Михайлов. Тема2. (wecompress.com).docx, 1 тема .docx, Презентация Тема №4.pdf, Саятов Саяс задание 4 тема.docx, ТЕст 5 тема.docx, тарих 1 лекция.docx, Календ. — темат. план по рус.яз. 6 класс.docx, 7 класс последняя тема.docx Показать все связанные файлы Подборка по базе: 10 тема тесты.docx, План конспект урока по Истории Средних веков тема урока_ _Кресто, 8. Гр. 7. Михайлов. Тема2. (wecompress.com).docx, 1 тема .docx, Презентация Тема №4.pdf, Саятов Саяс задание 4 тема.docx, ТЕст 5 тема.docx, тарих 1 лекция.docx, Календ. — темат. план по рус.яз. 6 класс.docx, 7 класс последняя тема.docxВидео:Эконометрика. Множественная регрессия и корреляция.Скачать  Тема 3. Нелинейная регрессия1. Модели нелинейной регрессии Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: гиперболы у = a + b/x + , параболы у = а + b x + c x 2 + и др. Различают два класса нелинейных регрессий: – регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; – регрессии, нелинейные по оцениваемым параметрам. Примером нелинейной регрессии по включенным в нее объясняющим переменным могут служить следующие функции: К нелинейным регрессиям по оцениваемым параметрам относятся функции: Нелинейная регрессия по включенным переменным не имеет никаких сложностей для оценки ее параметров. Они определяются, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе второй степени заменив переменные x = x1, x 2 = x2, получим двухфакторное уравнение линейной регрессии: для оценки параметров которого используется МНК Соответственно для полинома третьего порядка при замене x = x1, x 2 = x2, x З = x3 получим трехфакторную модель линейной регрессии а для полинома k-го порядка получим линейную модель множественной регрессии с k объясняющими переменными: Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничения в применении полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно меньше однородность совокупности по результативному признаку. Модели регрессии, нелинейные по оцениваемым параметрам, подразделяются на внутренне линейные и внутренне нелинейные. Если нелинейная модель внутренне линейна, то с помощью соответствующих преобразований она может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цены широко используется степенная функция где y – спрос (количество); x – цена; – случайная ошибка. Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры a и b неаддитивно. Однако её можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию e приводит его к линейному виду: Соответственно оценки параметров a и b могут быть найдены методом наименьших квадратов. В рассматриваемой степенной функции предполагается, что случайная ошибка мультипликативно связана с объясняющей переменной x. Если же модель представить в виде Внутренне нелинейной будет и модель вида потому что эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам. В специальных исследованиях по регрессионному анализу к нелинейным часто относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразования параметров могут быть приведены к линейному виду, относят к классу линейных моделей. Например, экспоненциальную модель y = e a + b x ; ибо, прологарифмировав её по натуральному основанию, получим линейную форму модели Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей итеративной процедуры. Модели внутренне нелинейные по параметрам, могут иметь место в эконометрических исследованиях; однако большее распространение получили модели, приводимые к линейному виду. Решение такого типа моделей реализовано в стандартных пакетах прикладных программ. По виду преобразования, которое используется для приведения модели к линейному виду, выделяют следующие группы моделей:
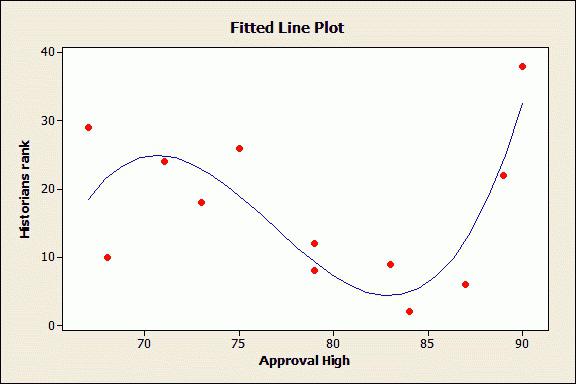
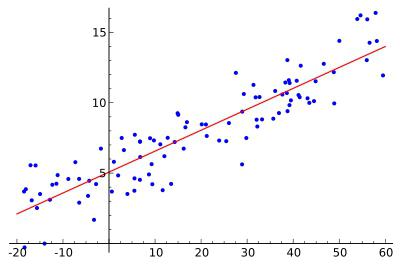
2. Выбор вида зависимости При выборе вида зависимости между двумя признаками нагляден графический метод, особенно для монотонных (не имеющих максимумы и минимумы) зависимостей. Наиболее характерные из них представлены на рис.2.4. Рис.2.4. Графики монотонных зависимостей При выборе зависимости во-первых, выбирается кривая, которая наиболее подходит для экспериментальных данных (исходя из аналитических предпосылок, либо визуально по графику), а во-вторых, если затруднительно выбрать одну из нескольких кривых, используют метод средних точек. В таблице приведены основные типовые формулы, наиболее часто встречающиеся в эконометрических исследованиях. Для каждой зависимости рассчитываются координаты средних точек Xk и Yk по формулам из таблицы. Средние точки наносят на график и выбирают ту формулу, средняя точка которой лежит ближе всего к экспериментальной кривой. | Формула | Xk | Yk | Приведение к линейному виду | |
| 1 | степенная |  |  |  | U = A + bZ; U = lgY; A = lga; Z = lgX |
| 2 | показательная |  |  |  | U = A + BX; U = lgY; A = lga; B = lgb |
| 3 | дробно-рациональная |  |  |  | |
| 4 | логарифмическая |  |  |  | Y = a + bZ; Z = lgX |
| 5 | гиперболическая |  |  |  | Y = a + bZ; Z = 1/X |
| 6 | функция спроса (Торнквиста) |  |  |  | U = A + BZ; U = 1/Y; Z = 1/X; A = 1/a; B = b/a |
3. Определение параметров уравнения регрессии
Рассмотрим нелинейные регрессии по оцениваемым параметрам. Пусть в результате наблюдения получен ряд изучаемого показателяX и Y. По этим значениям можно построить график.
| X | x1 | x2 | … | xn |
| Y | y1 | y2 | … | yn |
Затем необходимо определить параметры выбранной зависимости a и b таким образом, чтобы расчетная кривая лежала как можно ближе к экспериментальной кривой.
Для этого сначала необходимо привести уравнение регрессии к линейному виду. Это преобразование называется линеаризацией. Для этого необходимо ввести замену переменных согласно выбранной модели (в соответствии с таблицей). После введения новых переменных U и Z, необходимо рассчитать параметры A и В этого уравнения.
В качестве критерия близости S выбираем минимум суммы квадратов отклонений между экспериментальными и расчетными значениями. Учитывая, что в каждом конкретном случае линейный вид уравнения различный, запишем этот критерий в универсальном виде:
Для каждой формулы из табл. в этом критерии будут присутствовать разные переменные в зависимости от приведения их к линейному виду. Например, для первой формулы U = lgY; Z = lgX. Тогда система нормальных уравнений для определения параметров линейной зависимости будет иметь вид:

Для нахождения соответствующих сумм в каждом случае необходимо получить различные вспомогательные таблицы с учетом приведения выражений к линейному виду. Например, для второй формулы из табл.2.3 Zi = Xi, а Ui = lg(Yi) и т.д.
Решив эту систему, получаем искомые значения параметров. Следует отметить, что при нахождении параметров других зависимостей необходимо сначала привести их к линейному виду согласно табл.2.3.
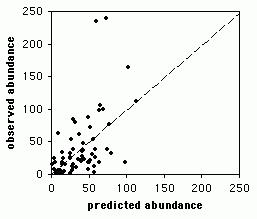
Для проверки правильности выполненных действий получаем расчетные значения подстановкой в найденную формулу экспериментальных значений X. Полученные расчетные значения наносим на график с экспериментальными данными и делаем вывод об адекватности.
| X | x1 | x2 | … | xn |
| Y | y1 р | y2 р | … | yn р |
Рассмотрим зависимость урожайности зерновых культур от количества внесенных удобрений:
| Внесено удобрений, ц/га, x | 1 | 2 | 3 | 4 | 5 |
| Урожайность, ц/га, y | 6 | 9 | 10 | 12 | 13 |
График экспериментальной кривой представлен на рисунке.
1) 

2) 
3) Xk = 3; 
4) Xk = 2,24; 
5) 
И наносим их на тот же график.
В связи с неровностью исходной кривой выбор зависимости неоднозначен – для учебных целей выбираем формулу 1: Y = a Х b . В линейном виде U = A + bZ; U = lg Y; A = lg a; Z = lg X.
Система нормальных уравнений имеет вид:
Находим коэффициенты этой системы. Для этого оформляем табл. 2.4
Таблица 2.4. Промежуточные результаты расчета
| X | Y | Z = logX | U = logY | Z 2 | Z U | Y р |
| 1 | 6 | 0,00 | 0,78 | 0,00 | 0,00 | 6,14 |
| 2 | 9 | 0,30 | 0,95 | 0,09 | 0,29 | 8,52 |
| 3 | 10 | 0,48 | 1,00 | 0,23 | 0,48 | 10,33 |
| 4 | 12 | 0,60 | 1,08 | 0,36 | 0,65 | 11,84 |
| 5 | 13 | 0,70 | 1,11 | 0,49 | 0,78 | 13,16 |
| 2,08 | 4,93 | 1,17 | 2,19 |







 ,
, , то она становится внутренне нелинейной, ибо её невозможно превратить в линейный вид.
, то она становится внутренне нелинейной, ибо её невозможно превратить в линейный вид. ,
, ,
, (и зависимая, и объясняющая переменные заданы в логарифмическом виде). Получается при линеаризации уравнения
(и зависимая, и объясняющая переменные заданы в логарифмическом виде). Получается при линеаризации уравнения  — лог-линейная. Получается при линеаризации уравнения
— лог-линейная. Получается при линеаризации уравнения  — линейно-логарифмическая. Сводится к линейной путем замены Z=lnX : Y= a +b · Z
— линейно-логарифмическая. Сводится к линейной путем замены Z=lnX : Y= a +b · Z . Сводится к линейной путем замены Z=1/X Y=a+b·Z+
. Сводится к линейной путем замены Z=1/X Y=a+b·Z+ .
.









 ;
;  .
.