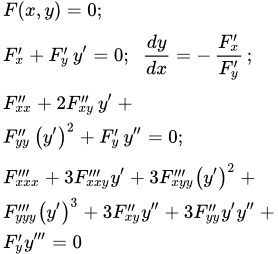Найти значение производной в точке неявной функции заданной уравнением

Видео:11. Производная неявной функции примерыСкачать

Производная неявной функции онлайн

Неявная функция — это функция, например , заданная в виде уравнения:

F ( x , y ( x ) ) = 0

Как правило, вместо уравнения F ( x , y ( x ) ) = 0 пишут просто F ( x , y ) = 0 подразумевая, что есть функция от .

В качестве примера неявного задания функции, можно привести уравнение окружности:

уравнение декартового листа:

x 3 + y 3 = 3 ∙ a ∙ x ∙ y ( a = const ≠ 0 ) ,

и т.д. Все эти примеры можно записать в виде уравнения F ( x , y ) = 0 : уравнение окружности: F ( x , y ) = x 2 + y 2 − a 2 = 0 , уравнение декартового листа: F ( x , y ) = x 3 + y 3 − 3 ∙ a ∙ x ∙ y = 0 .

В связи с тем, что для исследования любой функции (в том числе и заданной неявно) необходимо вычислять производную, задача нахождения производной функции заданной неявно возникает довольно часто. Так, как же найти производную неявной функции? Исчерпывающий ответ на этот вопрос вы получите, воспользовавшись нашим онлайн калькулятором.
Для того, чтобы решить вашу задачу, для начала перепишите свою функцию в виде уравнения F ( x , y ) = 0 . Как это сделать, подробно описано выше (нужно просто перенести все слагаемые в левую часть уравнения, оставив справа ). Далее вам необходимо определиться, как у вас обозначается переменная и как обозначается функция, которая зависит от этой переменной. В приведенных выше примерах, — переменная, — функция, зависящая от .
Затем, вам необходимо ввести свое уравнение F ( x , y ) в наш онлайн калькулятор и получить решение вашей задачи.

Видео:18+ Математика без Ху!ни. Производная неявной функции.Скачать

Производная функции, заданной неявно

Видео:11.1. Касательная к неявной функции / производная неявной функции ПРИМЕРЫСкачать

Производная первого порядка

Пусть функция задана неявным образом с помощью уравнения
(1) .
И пусть это уравнение, при некотором значении , имеет единственное решение . Пусть функция является дифференцируемой функцией в точке , причем
.
Тогда, при этом значении , существует производная , которая определяется по формуле:
(2) .

Доказательство

Для доказательства рассмотрим функцию как сложную функцию от переменной :
.
Применим правило дифференцирования сложной функции и найдем производную по переменной от левой и правой частей уравнения
(3) :
.
Поскольку производная от постоянной равна нулю и , то
(4) ;
.

Видео:27. Дифференцирование неявной функции двух переменныхСкачать

Производные высших порядков

Перепишем уравнение (4), используя другие обозначения:
(4) .
При этом и являются сложными функциями от переменной :
;
.
Зависимость определяет уравнение (1):
(1) .

Поскольку производная правой части уравнения (4) равна нулю, то
(5) .
Подставив сюда производную , получим значение производной второго порядка в неявном виде.

Дифференцируя, аналогичным образом, уравнение (5), мы получим уравнение, содержащее производную третьего порядка :
.
Подставив сюда найденные значения производных первого и второго порядков, найдем значение производной третьего порядка.

Продолжая дифференцирование, можно найти производную любого порядка.

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Примеры

Пример 1

Найдите производную первого порядка от функции, заданной неявно уравнением:
(П1) .

Решение по формуле 2

Находим производную по формуле (2):
(2) .

Перенесем все переменные в левую часть, чтобы уравнение приняло вид .
.
Отсюда .

Находим производную по , считая постоянной.
;
;
;
.

Находим производную по переменной , считая переменную постоянной.
;
;
;
.

По формуле (2) находим:
.

Мы можем упростить результат если заметим, что согласно исходному уравнению (П.1), . Подставим :
.
Умножим числитель и знаменатель на :
.

Решение вторым способом

Решим этот пример вторым способом. Для этого найдем производную по переменной левой и правой частей исходного уравнения (П1).

Подставим (из уравнения (П1)):
.
Умножим на :
.

Пример 2

Найти производную второго порядка от функции , заданной неявно с помощью уравнения:
(П2.1) .

Дифференцируем исходное уравнение, по переменной , считая что является функцией от :
;
.
Применяем формулу производной сложной функции.
.

Дифференцируем исходное уравнение (П2.1):
;
.
Из исходного уравнения (П2.1) следует, что . Подставим :
.
Раскрываем скобки и группируем члены:
;
(П2.2) .
Находим производную первого порядка:
(П2.3) .

Чтобы найти производную второго порядка, дифференцируем уравнение (П2.2).
;
;
;
.
Подставим выражение производной первого порядка (П2.3):
.
Умножим на :

;
.
Отсюда находим производную второго порядка.

Пример 3

Найти производную третьего порядка при от функции , заданной неявно с помощью уравнения:
(П3.1) .

Дифференцируем исходное уравнение по переменной считая, что является функцией от .
;
;
;
;
;
;
(П3.2) ;

Дифференцируем уравнение (П3.2) по переменной .
;
;
;
;
;
(П3.3) .

Из уравнений (П3.2), (П3.3) и (П3.4) находим значения производных при .
;
;
.

Автор: Олег Одинцов . Опубликовано: 16-02-2017

Видео:Производная неявной функцииСкачать

Производная фукнции, заданной неявно: руководство, примеры

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Как найти производную функции, заданной неявно

Будем учиться находить производные функций, заданных неявно. Что значит неявно? Сравним с обычной функцией. Обычная функция задана уравнением вида y=f(x) , где игрек, то есть функция, задан некоторым выражением, в котором присутствует икс. Таким образом, из переменных в левой части — только игрек, в правой — только икс. Если же функция задана неявно, то в левой части различные слагаемые с игреком «смешаны» с различными слагаемыми с иксом (или переменной, обозначенной другой буквой). Примеры функций, заданных неявно:

,

,

,

,

.

При этом и икс, и игрек могут быть в различных степенях, а в одном слагаемом могут быть и игрек, и икс.

Если функция задана неявно, то как получить игрек, то есть явную функцию? Просто: выразить игрек через другую переменную, то есть получить в левой части только игрек. А если нужно найти производную функции, заданной неявно, то есть получить в левой части только игрек со штрихом? Нужно сначала найти производные обеих частей уравнения, то есть продифференцировать их. А затем выразить производную игрека через производные других переменных.

Теперь приведенный выше «скелет» решения обрастет «мясом», то есть необходимыми подробностями. Те слагаемые, в которых присутствует только икс, обратятся в обычную производную функции от икса. А слагаемые, в которых присутствуют и икс, и игрек, нужно дифференцировать, пользуясь правилом дифференцирования сложной функции, то есть учитывать, что игрек — это функция от икса. Если совсем просто, то в полученной производной слагаемого с иксом должно получиться: производная функции от игрека, умноженная на производную от игрека. Например, производная слагаемого запишется как , производная слагаемого запишется как . Далее из всего этого нужно выразить этот «игрек штрих» и будет получена искомая производная функции, заданной неявно. Разберём это на примерах.

Видео:Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Решаем задачи вместе

Пример 1. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу, считая, что игрек — функция от икса:

.

Отсюда получаем производную, которая требуется в задании:

.

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.

y = f(x) . Так, например, заданные неявно функции

и

не выражаются через элементарные функции, то есть эти уравнения нельзя разрешить относительно игрека. Поэтому и существует правило дифференцирования функции, заданной неявно, которое мы уже изучили и далее будем последовательно применять в других примерах.

Пример 2. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу:

.

Выражаем игрек штрих и — на выходе — производная функции, заданной неявно:

.

Пример 3. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу:

.

Выражаем и получаем производную:

.

Решение производной функции, заданной неявно, можно проверить на онлайн калькуляторе.

Пример 4. Найти производную функции, заданной неявно:

.

Решение. Дифференцируем обе части уравнения по иксу:

.

Выражаем и получаем производную:

.

Пример 5. Найти производную функции, заданной неявно:

.

Решение. Переносим слагаемые в правой части уравнение в левую часть и справа оставляем ноль. Дифференцируем обе части уравнения по иксу:

Путь к ответу и в конец сам ответ:

Видео:ЕГЭ 2017 Профильный №7 найти производную в точке касания #7Скачать

Решить задачи самостоятельно, а затем посмотреть решения

Пример 6. Найти производную функции, заданной неявно:

Пример 7. Найти производную функции, заданной неявно:

Пример 8. Найти производную функции, заданной неявно:

📹 Видео

Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Производная функции заданной неявноСкачать

Производная в точке. Алгебра 10 и 11 класс.Скачать

Первая и вторая производная неявной функцииСкачать

Как находить производную неявной функции - bezbotvyСкачать

[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Найти значение производной в точке.Скачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать