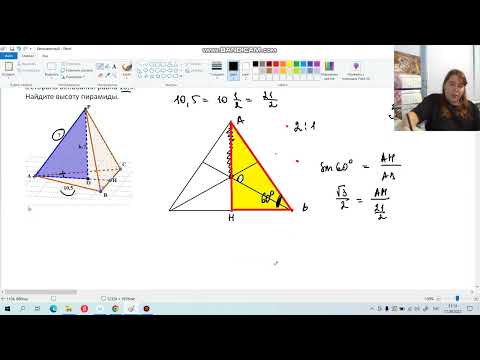
Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.
В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.
Содержание этой статьи:
- Теория
- Правильная пирамида
- Основные свойства
- Четырехугольная пирамида
- Треугольная пирамида
- Необходимые знания для нахождения высоты
- Формулы для нахождения высоты
- ВИДЕО: Примеры решения задач
- Нахождение высоты в правильной пирамиде
- Треугольная пирамида
- Четырехугольная пирамида
- Часто задаваемые вопросы
- Типичные ошибки на ЕГЭ
- Полезные советы
- Онлайн решение Пирамиды по координатам вершин
- Как найти высоту пирамиды по векторам
- Ответ
- Проверено экспертом
- 💡 Видео
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
Теория
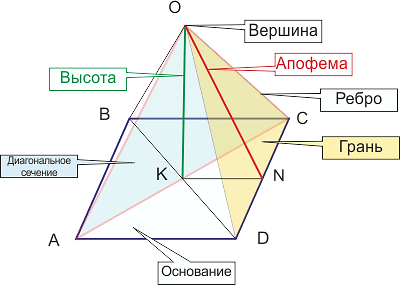
Правильная пирамида
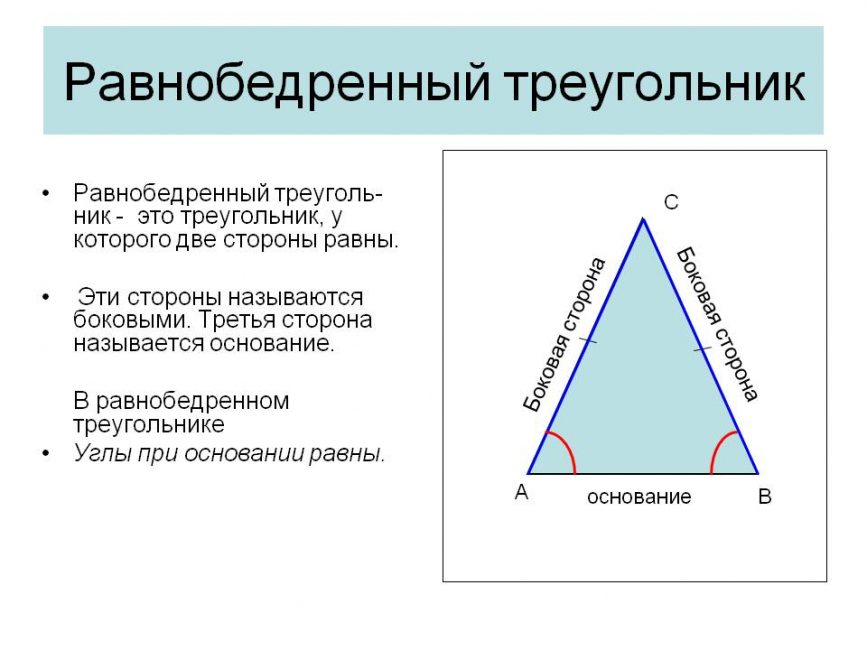
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.
Для решения задач понадобится знать теоремы равнобедренного треугольника:
Основные свойства
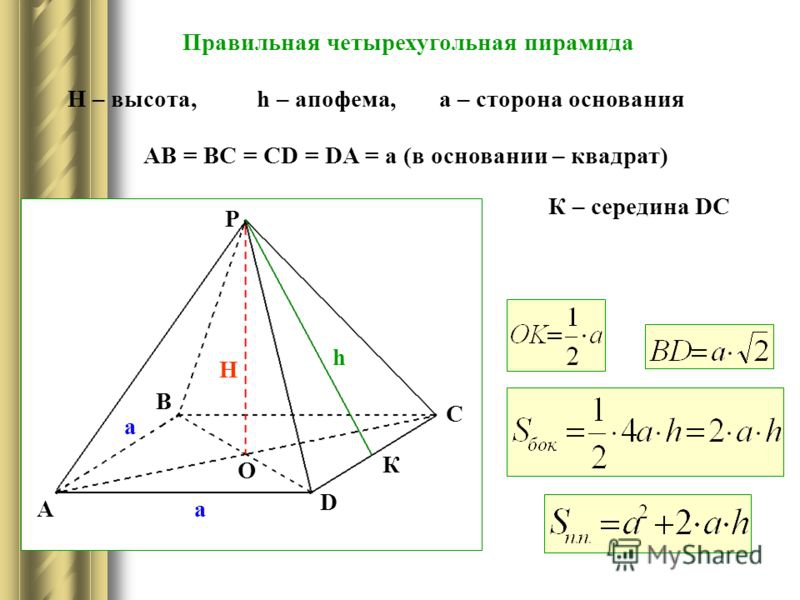
Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.
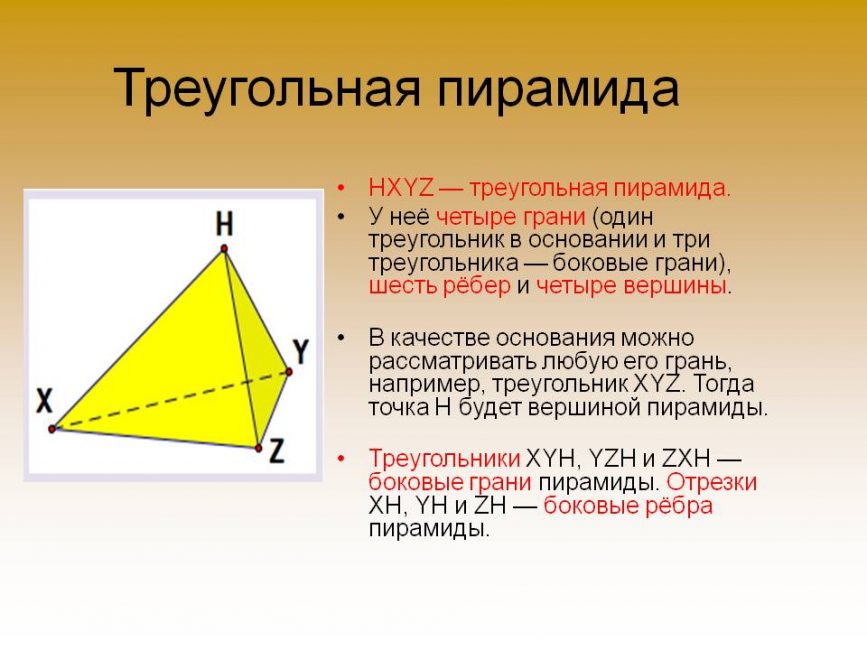
Треугольная пирамида
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.
Необходимые знания для нахождения высоты
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты
Запомните, что маленькая буква h – это апофема, а большая H – высота.
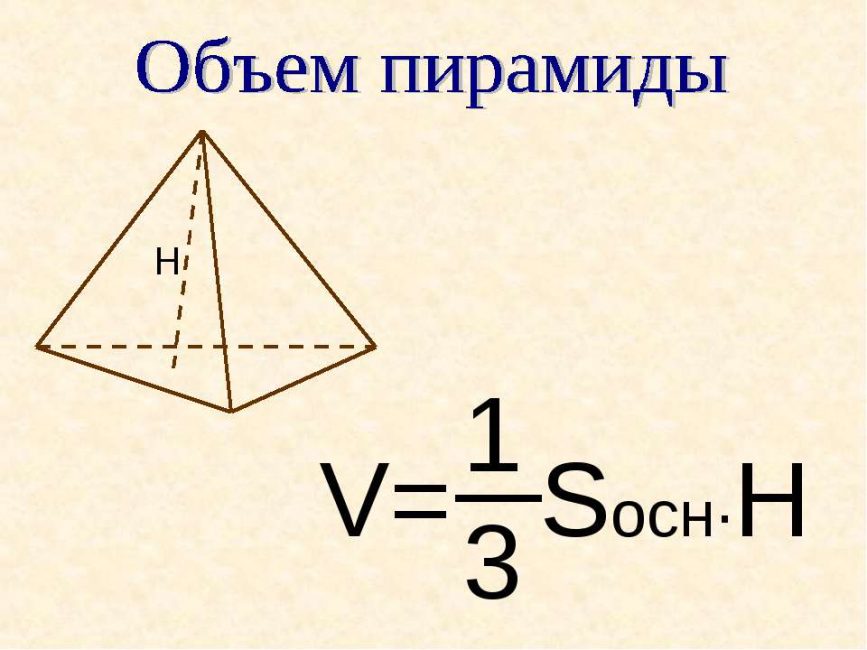
В некоторых задачах, высоту можно найти через объем:
ВИДЕО: Примеры решения задач
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
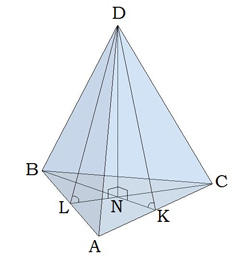
Треугольная пирамида
Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
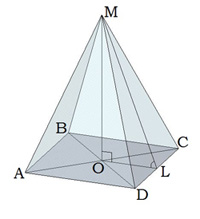
Четырехугольная пирамида
Задача 1
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Задача 4
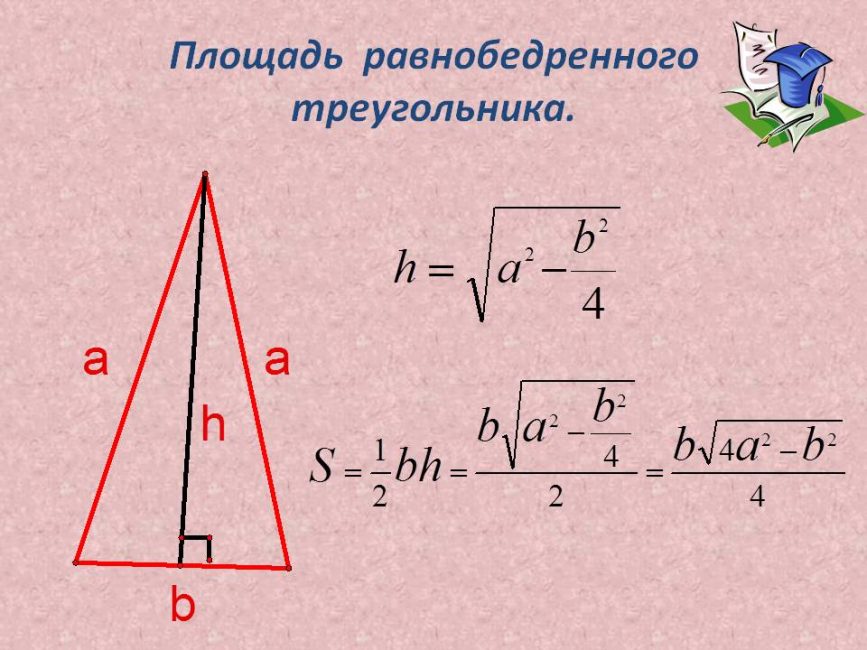
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.
Площадь равнобедренного треугольника
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Видео:Уравнения стороны треугольника и медианыСкачать
Часто задаваемые вопросы
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
Если выразить высоту через формулу объема, то получится следующее:
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать
Типичные ошибки на ЕГЭ
Видео:Вычисляем высоту через координаты вершин 1Скачать
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи! Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!
Видео:10 класс, 33 урок, Правильная пирамидаСкачать
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Уравнение высоты пирамидыСкачать  Как найти высоту пирамиды по векторамИнструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти.
Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж. Пример №2 . В тетраэдре ABCD вычислить:
A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1) Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать  ОтветПроверено экспертом
Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) . Находим векторы АВ, АС и АД. Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258. Определяем векторное произведение АВ х АС. -6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0). Далее находим смешанное произведение (АВ х АС) х АД. (АВ х АС) = (-5; -10; 0), (АВ х АС) х АД = 30 + 10 + 0 = 40. Объем пирамиды равен (1/6) этого произведения: V = (1/6)*40 = (20/3) куб.ед. Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC). Площадь основания АВС равна половине модуля векторного произведения АВ х АС. S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед. h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777. 1) чертёж пирамиды по координатам её вершин; 2) длины и уравнения рёбер, медиан, апофем, высот; 3) площади и уравнения граней; 4) система линейных неравенств, определяющих пирамиду; 5) основания и точка пересечения медиан (центроид); 6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням; 7) объём пирамиды; 8) основания, площади и уравнения биссекторов; 9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные; 10) параметры и уравнения вписанной и описанной сфер; Внимание! Этот сервис может не работать в браузере Internet Explorer. Запишите координаты вершин пирамиды и нажмите кнопку. | A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | ||
