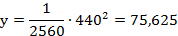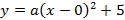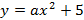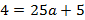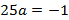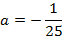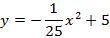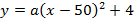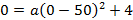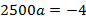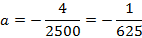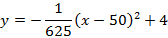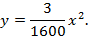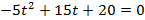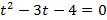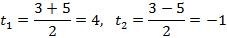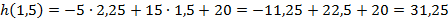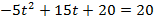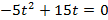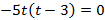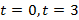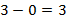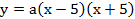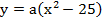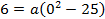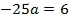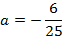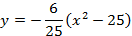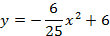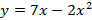Видео:Задача про арку Как рассчитать высоту опор арочного мостаСкачать

Ваш ответ
Видео:Вычисляем высоту через координаты вершин 1Скачать

Похожие вопросы
- Все категории
- экономические 43,407
- гуманитарные 33,633
- юридические 17,905
- школьный раздел 608,009
- разное 16,855
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Задача 31453 Пожалуйста помогите 1)определить.
Условие
Пожалуйста помогите
1)определить величину параметра расположение относительно координатных оси следующих парабол: y^2=6x x^2=5y
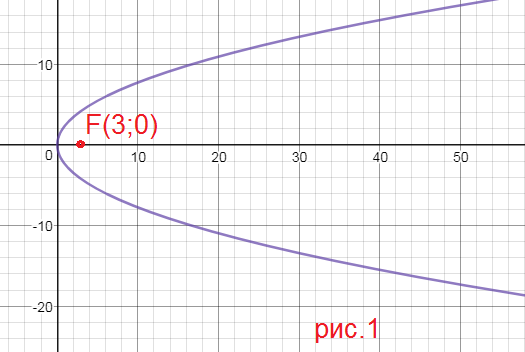
2)найти фокус и уравнение директрисы параболы y^2=24x
Решение
Канонические уравнения параболы:
x^2=2py cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
Фокус F(0;p/2)
Уравнение директрисы:
y=-p/2
x^2=-2py cимметрична относительно оси Оу, ветви направлены в сторону противоположную оси Оу
Фокус F(0;-p/2)
Уравнение директрисы:
y= p/2
y^2=2px cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(p/2;0)
Уравнение директрисы:
x=-p/2
y^2=-2px cимметрична относительно оси Ох, ветви направлены в сторону противоположную оси Ох
Фокус F(-p/2;0)
Уравнение директрисы:
x=p/2
[b]Решение[/b]:
1) y^2=6x ⇒ 2p=6;
p=3
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
x^2=5y 2p=5 ⇒ 2p=5;
p=2,5
cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
2)
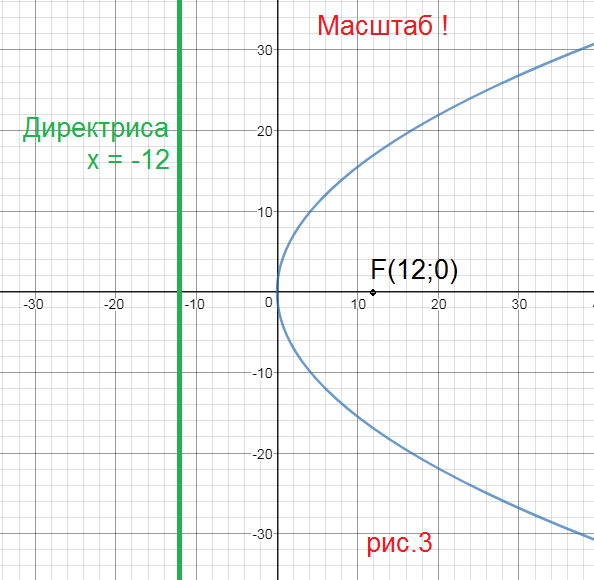
y^2=24x ⇒ 2p=24;
p=12
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(12;0)
Уравнение директрисы:
x=-12
см. рис.3 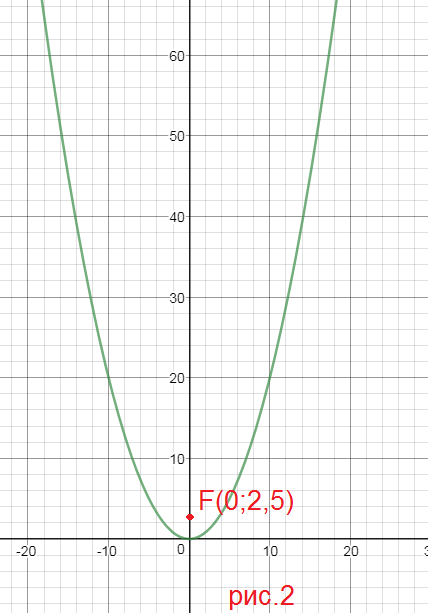
Видео:Задача 6 №27612 ЕГЭ по математике. Урок 62Скачать

Урок_3_Решение текстовых задач_Методические рекомендации
Методические рекомендации к уроку №3
темы/подраздела « Квадратичная функция и ее график »
раздела « Квадратичная функция»
Тема урока: Решение текстовых задач
8. 4 .2.3 использовать квадратичную функцию для решения прикладных задач;
8.4.3.1 составлять математическую модель по условию задачи.
На данном уроке учащиеся продолжат работу по развитию навыка решения задач с использованием квадратичной функции.
Методические рекомендации по организации урока. Рекомендации по формативному оцениванию
В начале урока учащимся предлагается тестовые задания для организации повторения пройденного материала. Учитель заранее готовит сигнальные карточки трех цветов для каждого ученика. Их использование позволит учителю быстро оценить понимание учащимися определенного материала. Допущенные ошибки сразу анализируются.
Затем проводится письменная работа, она с совместного разбора задания на составление уравнения функции и поиска ответа на вопрос задачи. Учитель вовлекает всех учащихся в диалог. Для первоначального закрепления учащиеся решают задачу в группах. Здесь нужно нацелить их на то, что каждый ученик после обсуждения должен уметь объяснить решение задачи свой группы. Процесс объяснения другим учащимся позволит глубже разобраться в решении. Также здесь нужно поощрять учащихся, задающих вопросы. Учитель обходит класс, слушает объяснения, помогает в корректном применении математического языка.
Два задания подготовлены для самостоятельного решения учащимися. Учитель обходит класс, дает советы учащимся. Он может также привлекать других учащихся для консультирования тех, кто испытывает затруднения.
Ответы и решения
Мост Голден Гейт через пролив Золотые ворота находится в Сан-Франциско (США). Мост построен по проекту инженера Йозефа Штрауса. Строительство началось в 1933 году и было закончено через 4 года. Мост установил два рекорда: как самый длинный и как самый высокий мост.
Длина основного пролета моста (расстояние между опорами) 1280 м, высота опор над уровнем проезжей части моста – 160 м. Кабель, поддерживающий мост, имеет форму параболы и касается проезжей части в середине пролета. На какой высоте находится кабель на расстоянии 200 м от опоры моста?
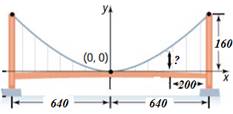
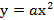
Точка (640, 160) – расположена на одной из опор, отсюда 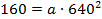
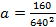
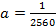
Тогда уравнение параболы имеет вид: 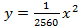
Кабель находится на расстоянии 200 м от опоры моста, следовательно, в 440 м от вершины параболы.
Задание для группы 1
Дорога проходит под параболической аркой, как показано на рисунке. Самая высокая часть арки – 5 м. Ширина дороги – 10м, а высота – 4 м. Составьте квадратичную функцию, задающую форму арки.
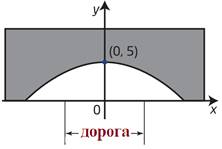
Запишем уравнение параболы в виде 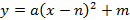
Ширина дороги – 10м, а высота – 4 м, значит парабола проходит через точку 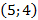
Ответ : 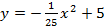
Задание для группы 2
Небольшие мосты имеют форму параболы. На рисунке представлен один из таких мостов. Составьте уравнение параболы, определяющей форму этого моста.
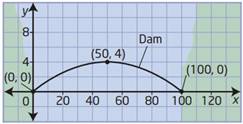
Запишем уравнение параболы в виде 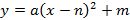
Парабола проходит через точки 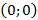
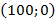
Ответ : 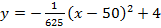
Задание для группы 3
Длина моста 400 м, а высота опор 75 м. Напишите уравнение параболы, являющейся моделью для подвесного кабеля, удерживающего этот мост.

Построим координатную плоскость, так чтобы ось х проходила вдоль проезжей части моста, а ось у – вдоль оси симметрии. Тогда вершина параболы имеет координаты (0, 0), значит функция задается формулой 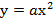
Парабола проходит через точку (200; 75), тогда 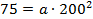
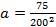
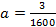
Тогда уравнение параболы имеет вид:
1. Тело брошено вертикально вверх. Высота ( h ), на которой находится тело через t секунд полета, вычисляется по формуле 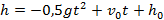
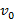
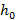
Составьте формулу, задающую эту зависимость, если h0 = 20, v0 = 15 и постройте график.
Используя график, ответьте на вопросы:
а) Сколько времени тело двигалось вверх?
б) Сколько времени тело двигалось вниз?
в) На какую максимальную высоту поднялось тело?
г) В течении какого времени тело находилось на высоте более 20 м?
Функция имеет вид 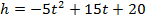
а) 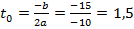
б )
Через 4 с тело упало на землю.
Тело двигалось вниз 2,5 с.
в)
г )
Ответ: Тело находилось на высоте более 20 м в течение 3 с.
2. Двух полосная дорога со встречным движением проходит под аркой шириной 10 м. Самая высокая точка арки расположена на высоте 6 м. Сможет ли грузовик, высота которого 4,5 м, а ширина 3 м, проехать под этой аркой? Ответ объясните.
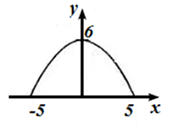
Если расположить координатную плоскость, так чтобы ось х проходила вдоль проезжей части дороги, а ось у – вдоль оси симметрии, тогда вершина параболы имеет координаты (0, 6) . Парабола проходит через точки 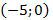
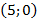
Подставив координаты точки 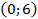
Ширина грузовика 3 м, тогда при 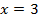
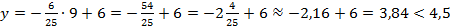
Ответ: Грузовик может проехать под этой аркой .
Найдите наибольшее или наименьшее значение функции.
a) 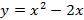
b) 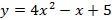
c)
Определите коэффициенты функции 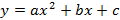
а) 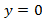
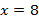
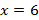
б) 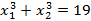
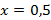
в) наименьшее значение функции, равное 7, достигается при 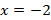
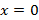
Список полезных ссылок и литературы
1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений. – М.: Мнемозина, 2010
2. Виленкин Н.Я., Сурвилло Г.С. Алгебра. 9 класс. учеб. Для учащихся с углубленным изучением математики. / 7-е изд. — М.: Просвещение, 2006.
🎦 Видео
213. Фокус и директриса параболы.Скачать

Видеоурок "Парабола"Скачать

Как легко составить уравнение параболы из графикаСкачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Длина окружности. Математика 6 класс.Скачать

Вершина параболы и ось симметрии. ПримерСкачать

С.М. Задача №3.1 Трёхшарнирная арка параболического очертанияСкачать

Парабола в архитектуреСкачать

№499. Найдите меньшую высоту треугольника со сторонами, равными: а) 24 см, 25 см, 7 см; б) 15Скачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

Найти центр и радиус окружностиСкачать

Лекция Zoom. Расчет трехшарнирных арок. Палагушкин В.ИСкачать

КАК НАЙТИ ВЫСОТУ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ЕСЛИ ИЗВЕСТЕН ОБЪЕМ, ДЛИНА И ШИРИНА? Пример 5 классСкачать

Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать