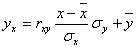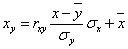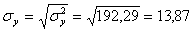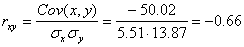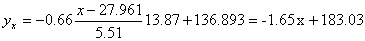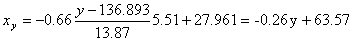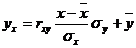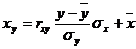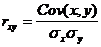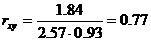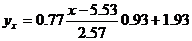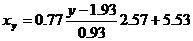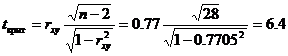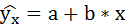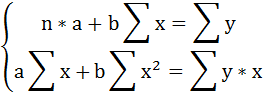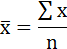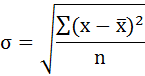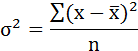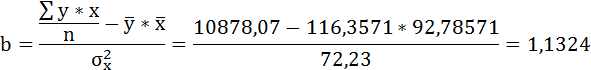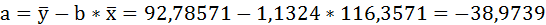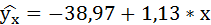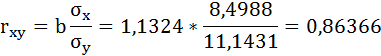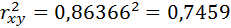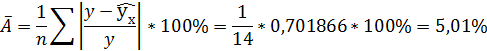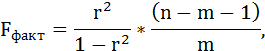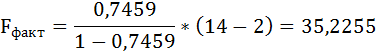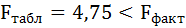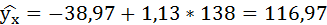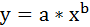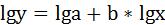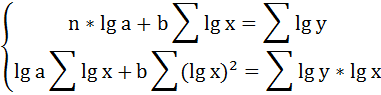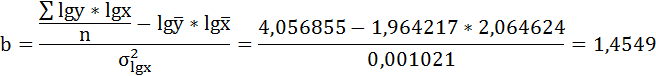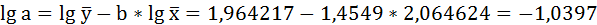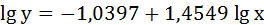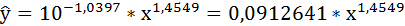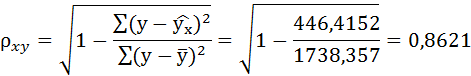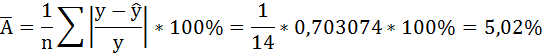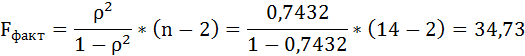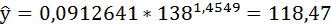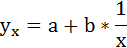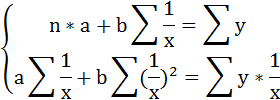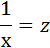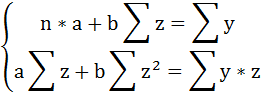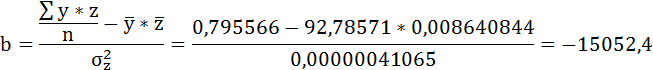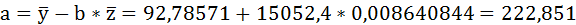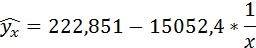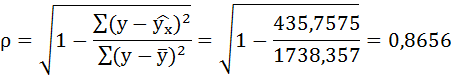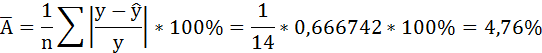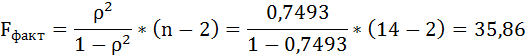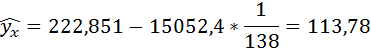Найти выборочные уравнения прямых линий регрессии по данным с таблицы (5 видео)

Корреляционная таблица

Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .

y/x	15	20	25	30	35	40
100	2	2
120	4	3	10	3
140	2	50	7	10
160	1	4	3
180	1	1

Решение:
Уравнение линейной регрессии с y на x будем искать по формуле

а уравнение регрессии с x на y, использовав формулу:

где x x , y — выборочные средние величин x и y, σ_x, σ_y — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 _x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 _y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
и
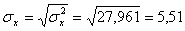
Определим коэффициент корреляции:

где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):

и уравнение x(y):

Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.

Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:

X / Y	2	4	6	8	10
1	5	4	2	0	0
2	0	6	3	3	0
3	0	0	1	2	3
5	0	0	0	0	1

Уравнение линейной регрессии с y на x имеет вид:

Уравнение линейной регрессии с x на y имеет вид:

найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 _x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 _y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σ_x = 2.57 и σ_y = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:

Запишем уравнения линий регрессии y(x):

и вычисляя, получаем:
y_x = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):

и вычисляя, получаем:
x_y = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим t_крит:
t_крит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.

Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение

Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.

Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4

Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7

Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение

Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.

X / Y	0	2	7	12	17	22	27	32	37	42
0	3	6	0	0	0	0	0	0	0	0
1	25	108	44	8	2	0	0	0	0	0
2	30	50	60	21	5	5	0	0	0	0
3	1	11	33	32	13	2	3	1	0	0
4	0	5	5	13	13	7	2	0	0	0
5	0	0	1	2	12	6	3	2	1	0
6	0	1	0	1	0	0	2	1	0	1
7	0	0	1	1	0	0	0	1	0	0

Решение.
Скачать решение

Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:

Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
Определить линии регрессии и построить их графики.

Скачать

Содержание

Задача по эконометрике 3
Найти выборочные уравнения прямых линий регрессии по данным с таблицы
Контакты
Задача №1 Построение уравнения регрессии
Требуется:
Решение:
📽️ Видео

Видео:Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Задача по эконометрике 3

Задача 3. Определить выборочное уравнение прямой линии регрессии Y на Х по данным корреляционной таблицы. Найти интервал для истинного значения коэффициента корреляции.

Так как данные наблюдений между признаками Х и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то для упрощения вычислений можем перейти к условным вариантам:

где С₁, С₂ – «ложные нули» вариант Х и Y соответственно (новые начала отсчета); h₁, h₂ – шаги (разности между двумя соседними вариантами).

С₁=40; h₁=10;

С₂=15; h₂=5;

Итого

Итого n_u

100

Вычислим групповые средние ū_i и ν_i

Определяем теперь χ и ȳ по формулам:

Вычислим коэффициент корреляции.

При переходе к условным вариантам коэффициент корреляции вычисляется по формуле:

Так как коэффициент корреляции положителен, то делаем вывод о положительной связи между рассматриваемыми признаками, т.е. с увеличением значений признака Х значения признака Y тоже растут.

Найдем уравнение прямой регрессии Y на Х по формуле:

— искомое выборочное уравнение прямой линии регрессии Y на Х

Найдем доверительный интервал для коэффициента корреляции при доверительной вероятности 0,95 по формуле:

Для k=n-2=100-2=98 t=t_табл=1,984

С вероятностью 0,95 истинное значение коэффициента корреляции лежит в пределах от 0,566 до 0,734.

Видео:Математика #1 | Корреляция и регрессияСкачать

Найти выборочные уравнения прямых линий регрессии по данным с таблицы

Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Найти выборочные уравнения прямых линий регрессии по данным с таблицы

Индекс розничных цен на продукты питания (х)	Индекс промышленного производства (у)
1	100	70
2	105	79
3	108	85
4	113	84
5	118	85
6	118	85
7	110	96
8	115	99
9	119	100
10	118	98
11	120	99
12	124	102
13	129	105
14	132	112

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

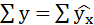
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмирование степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 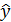. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz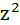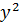
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.