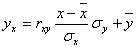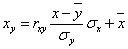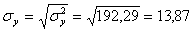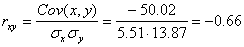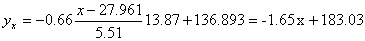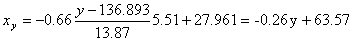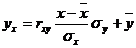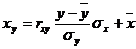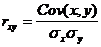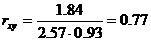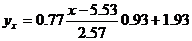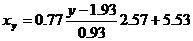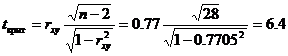Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
а уравнение регрессии с x на y, использовав формулу:
где x x , y — выборочные средние величин x и y, σx, σy — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
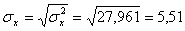
Определим коэффициент корреляции:
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
и уравнение x(y):
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | 0 | 0 |
| 2 | 0 | 6 | 3 | 3 | 0 |
| 3 | 0 | 0 | 1 | 2 | 3 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 0 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 0 | 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 25 | 108 | 44 | 8 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | 0 | 0 | 0 | 0 |
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | 0 | 0 |
| 4 | 0 | 5 | 5 | 13 | 13 | 7 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Скачать
- Калькулятор линейной регрессии
- Подробнее об этом калькуляторе линейной регрессии
- Калькулятор линейной регрессии Шаги
- Остатки регрессии
- Другие калькуляторы, относящиеся к линейной регрессии
- Расчет линейной регрессии онлайн
- Общая характеристика линейной регрессии
- Формулы уравнения и коэффициентов линейной регрессии
- Пример расчета уравнения регрессии
- Онлайн калькулятор расчета уравнения регрессии
- Заказать решение задач на построение уравнения регрессии
- 🔍 Видео
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Видео:Математика #1 | Корреляция и регрессияСкачать

Калькулятор линейной регрессии
Инструкции: Выполните регрессионный анализ с помощью Калькулятор линейной регрессии , где будет найдено уравнение регрессии и будет предоставлен подробный отчет о расчетах вместе с диаграммой рассеяния. Все, что вам нужно сделать, это ввести данные X и Y. При желании вы можете добавить заголовок и имя переменных.
Видео:Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать

Подробнее об этом калькуляторе линейной регрессии
А модель линейной регрессии соответствует модели линейной регрессии, которая минимизирует сумму квадратов ошибок для набора пар ((X_i, Y_i)).
Уравнение линейной регрессии, также известное как уравнение наименьших квадратов, имеет следующую форму: (hat Y = a + b X), где коэффициенты регрессии (a) и (b) вычисляются этим калькулятором регрессии следующим образом:
[b = frac<SS_><SS_>] [a = bar Y — bar X cdot b ]
Коэффициент (b) известен как коэффициент наклона, а коэффициент (a) известен как пересечение оси y.
Если вместо линейной модели вы хотите использовать нелинейную модель, вам следует рассмотреть возможность использования калькулятор полиномиальной регрессии , что позволяет использовать степени независимой переменной.
Калькулятор линейной регрессии Шаги
Шаги для проведения регрессионного анализа:
(1) Получите данные для зависимой и независимой переменных в формате столбца.
(2) Введите данные в формате, разделенном запятыми или пробелами.
(3) Нажмите «Рассчитать».
Остатки регрессии
Как мы можем оценить, насколько хороша модель линейной регрессии? Вы можете подумать «легко, просто посмотрите на диаграмма рассеяния «. На самом деле математика и статистика имеют тенденцию выходить за рамки того, где глаз встречается с графиком. Обычно рискованно полагаться только на диаграмму рассеяния для оценки качества модели.
С точки зрения качества соответствия один из способов оценки качества соответствия модели линейной регрессии состоит в следующем: вычисление коэффициента детерминации , указывает долю вариации зависимой переменной, которая объясняется независимой переменной.
В линейной регрессии выполнение допущений имеет решающее значение, поэтому оценки коэффициента регрессии имеют хорошие свойства (среди прочего, несмещенность, минимальная дисперсия).
Чтобы оценить предположения линейной регрессии, вам нужно будет взглянуть на остатки. Для этого вы можете взглянуть на наши калькулятор остатка .
Другие калькуляторы, относящиеся к линейной регрессии
Вас также может заинтересовать вычисление коэффициента корреляции , или в построить диаграмму рассеяния с предоставленными данными.
Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Расчет линейной регрессии онлайн
Быстрая навигация по странице:
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Общая характеристика линейной регрессии
Под линейной регрессией понимается функция вида Y = a0 + a1X1 + a2X2 + … anXn, объясняющая изменение величины зависимой (или эндогенной) переменной Y от изменения величин объясняющих (независимых) переменных X1, X2, … Xn. В том случае, когда в построенной функции объясняющая переменная (или фактор) X только одна, то тогда такую регрессию называют парной, если же в модели используется несколько факторных переменных X – то множественной регрессией. Особенностью линейной регрессии является то, что изменение (приращение) зависимой переменной Y пропорционально изменению объясняющих факторов X, а графиком такой регрессии является прямая линия. Расчет параметров линейной регрессии выполняется, как правило, при помощи метода наименьших квадратов (МНК). Качество построенной модели во многом зависит от количества значений наблюдений, используемых для построения уравнения линейной регрессии.
Размещено на www.rnz.ru
Видео:Парная регрессия: линейная зависимостьСкачать

Формулы уравнения и коэффициентов линейной регрессии
Общая формула парной линейной регрессии следующая:
Y^ = a + b*x + ε
где: Y^ — теоретические (расчетные) значения зависимого показателя (зависимой переменной), получаемые по построенному уравнению;
a — свободный член уравнения регрессии;
b — коэффициент уравнения регрессии
Для нахождения параметров (коэффициентов) линейной регрессии существует множество формул. Приведем некоторые из них:
— формулы для нахождения свободного члена уравнения регрессии a:
 |  |
— формулы для нахождения коэффициента регрессии b:
 |  |  |
Для расчета параметров уравнения регрессии также можно решить следующую систему уравнений:
Видео:Как вычислить линейный коэффициент корреляции в MS Excel и построить уравнение регрессии?Скачать

Пример расчета уравнения регрессии
Приведем пример расчета параметров уравнения регрессии для значений, приведенных в следующей таблице (пример условный):
По семи территориям Уральского региона известны значения двух признаков за 201_ год:
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, y | Среднедневная заработная плата одного работающего, руб., х |
|---|---|---|
| Удмуртская республика | 66.3 | 41.5 |
| Свердловская область | 59.9 | 57.7 |
| Республика Башкортостан | 57.3 | 55.8 |
| Челябинская область | 53.1 | 59.4 |
| Пермский край | 51.7 | 56.7 |
| Курганская область | 50.7 | 44.6 |
| Оренбургская область | 48 | 52.7 |
1. Для характеристики зависимости y от x рассчитать параметры уравнения парной линейной регрессии;
2. Рассчитать линейный коэффициент парной корреляции и дать его интерпретацию;
3. Рассчитать коэффициент детерминации и дать его интерпретацию;
4. Рассчитать коэффициент эластичности для линейной парной регрессии и дать его интерпретацию.
Для построения уравнения парной линейной регрессии составим таблицу вспомогательных расчетов, где будут произведены необходимые промежуточные вычисления:
| № района | Расходы на покупку продовольственных товаров в общих расходах, %, y | Среднедневная заработная плата одного работающего, руб., х | yx |
|---|---|---|---|
| 1 | 66.3 | 41.5 | 2751.45 |
| 2 | 59.9 | 57.7 | 3456.23 |
| 3 | 57.3 | 55.8 | 3197.34 |
| 4 | 53.1 | 59.4 | 3154.14 |
| 5 | 51.7 | 56.7 | 2931.39 |
| 6 | 50.7 | 44.6 | 2261.22 |
| 7 | 48 | 52.7 | 2529.6 |
| Итого | 387 | 368.4 | 20281.37 |
| Среднее значение | 55.29 | 52.63 | 2897.34 |
| σ | 5.84 | 6.4 | — |
| σ 2 | 34.06 | 40.93 | — |
Далее рассчитаем коэффициенты уравнения парной линейной регрессии.
Коэффициент b вычислим по формуле:

Пример расчета коэффициента b уравнения парной линейной регрессии: b = (2897.34-55.29*52.63)/40.93 = -0.31
Коэффициент a вычислим по формуле:

Пример расчета коэффициента a уравнения парной линейной регрессии: a = 55.29 — -0.31*52.63 = 71.61
Получим следующее уравнение парной линейной регрессии:
Линейный коэффициент парной корреляции рассчитаем по формуле:

Пример расчета линейного коэффициента парной корреляции:
ryx = -0.31*6.4 / 5.84 = -0.3397
Далее вычислим коэффициент детерминации по формуле:

Пример расчета значения коэффициента детерминации:
r 2 yx = -0.3397*-0.3397 = 0.1154 или 11.54%
Интерпретация значения коэффициента детерминации: согласно полученному значению коэффициента детерминации вариация расходов на покупку продовольственных товаров в общих расходах только на 11.54% определяется вариацией среднедневной заработной платой одного работающего, что является низким показателем.
Далее рассчитаем коэффициент эластичности для линейной регресии по формуле:

Пример расчета величины коэффициента эластичности для линейной регрессии:
Интерпретация значения коэффициента эластичности для линейной регрессии: полученное значение коэффициента эластичности показывает, что с изменением среднедневной заработной платы одного работающего на 1% от своего среднего значения величина расходов на покупку продовольственных товаров изменится на -0.295% в среднем по совокупности.
Далее рассчитаем значение F-критерия Фишера для построенного уравнения парной линейной регрессии. Расчет F-критерия Фишера выполним по формуле:

Пример расчета F-критерия Фишера: F = 0.1154 / 0.8846*5 = 0.65.
Интерпретация значения F-критерия Фишера. Так как полученное значение F-критерия Фишера меньше табличного критерия, то полученное уравнение парной линейной регрессии является статистически незначимым и не пригодным для описания зависимости доли расходов на покупку продовольственных товаров в общих расходах только от величины среднедневной заработной платой одного работающего. Показатель тесноты связи также признается статистически незначимым.
Видео:Линейная регрессияСкачать

Онлайн калькулятор расчета уравнения регрессии
В заключении приводим небольшой онлайн калькулятор расчета параметров уравнения линейной регрессии, используя который, Вы можете самостоятельно определить значения соответствующих коэффициентов и построить линейную регрессии онлайн. При заполнении приведенной формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить построить уравнение регрессии онлайн быстро и точно. В приведенной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает. Для определения значений соответствующих показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!
Приведенная форма рассчитана на ввод максимум 10 значений. Если у вас их меньше, то обязательно оставьте «лишние» поля формы пустыми!
Онлайн-калькулятор расчета коэффициента корреляции:
Видео:Корреляционная таблицаСкачать
Заказать решение задач на построение уравнения регрессии
Мы можем помочь Вам выполнить построение различных уравнений регрессии, как линейных, так и нелинейных:
🔍 Видео
Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Лекция 8. Линейная регрессияСкачать

Уравнение прямой по графику. ПримерыСкачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Множественная Линейная Регрессия || Машинное ОбучениеСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Линейная регрессияСкачать