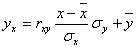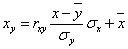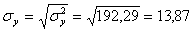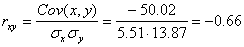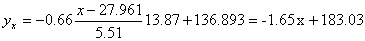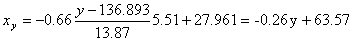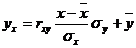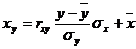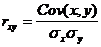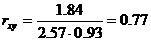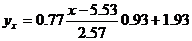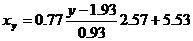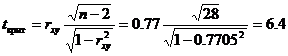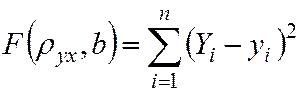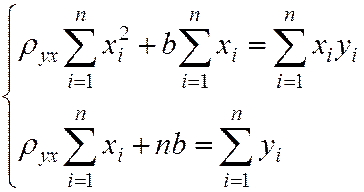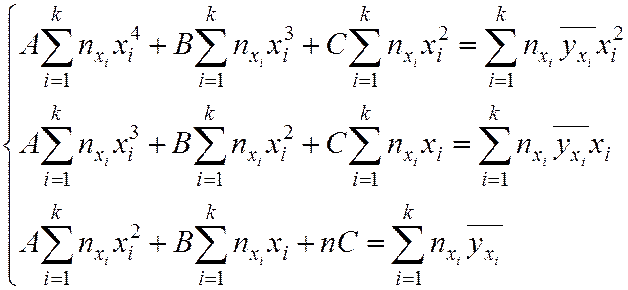Найти выборочное уравнение прямой линии регрессии на по данным таблицы (2 видео)

Содержание

Корреляционная таблица
Выборочное уравнение прямой линии регрессии
Задача по эконометрике 3
📹 Видео

Видео:Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать

Корреляционная таблица

Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .

y/x	15	20	25	30	35	40
100	2	2
120	4	3	10	3
140	2	50	7	10
160	1	4	3
180	1	1

Решение:
Уравнение линейной регрессии с y на x будем искать по формуле

а уравнение регрессии с x на y, использовав формулу:

где x x , y — выборочные средние величин x и y, σ_x, σ_y — выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 _x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 — 27.961 2 = 30.31
σ 2 _y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 — 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
и
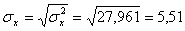
Определим коэффициент корреляции:

где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 — 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):

и уравнение x(y):

Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.

Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:

X / Y	2	4	6	8	10
1	5	4	2	0	0
2	0	6	3	3	0
3	0	0	1	2	3
5	0	0	0	0	1

Уравнение линейной регрессии с y на x имеет вид:

Уравнение линейной регрессии с x на y имеет вид:

найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 _x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 — 5.53 2 = 6.58
σ 2 _y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 — 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σ_x = 2.57 и σ_y = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 — 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:

Запишем уравнения линий регрессии y(x):

и вычисляя, получаем:
y_x = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):

и вычисляя, получаем:
x_y = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим t_крит:
t_крит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.

Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение

Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.

Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4

Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X — величина месячной прибыли в тыс. руб., Y — месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7

Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение

Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y — усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.

X / Y	0	2	7	12	17	22	27	32	37	42
0	3	6	0	0	0	0	0	0	0	0
1	25	108	44	8	2	0	0	0	0	0
2	30	50	60	21	5	5	0	0	0	0
3	1	11	33	32	13	2	3	1	0	0
4	0	5	5	13	13	7	2	0	0	0
5	0	0	1	2	12	6	3	2	1	0
6	0	1	0	1	0	0	2	1	0	1
7	0	0	1	1	0	0	0	1	0	0

Решение.
Скачать решение

Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:

Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
Определить линии регрессии и построить их графики.

Скачать

Видео:Парная регрессия: линейная зависимостьСкачать

Выборочное уравнение прямой линии регрессии

Рассмотрим выборочное уравнение прямой линии среднеквадратичной регрессии Y на X в виде

, (7.3)

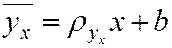
где 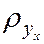– угловой коэффициент прямой линии регрессии, который называют выборочным коэффициентом регрессии Y на X; он является оценкой коэффициента регрессии (раздел 4.4).

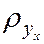
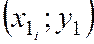
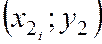
Подберём параметры и b таким образом, чтобы точки , ,…, , построенные на плоскости XоY, лежали как можно ближе к прямой (7.3).

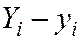
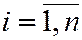
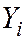
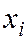
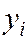
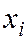
При использовании метода наименьших квадратов (МНК) смысл этого требования интерпретируется так: сумма квадратов отклонений должна быть минимальной. Под отклонением понимают разность , , где – вычисленная по уравнению (7.3) ордината наблюдаемого значения ; – наблюдаемая ордината, соответствующая .

Запишем это требование в виде функции:

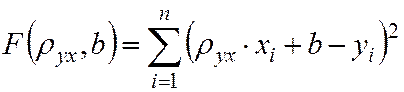
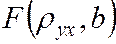
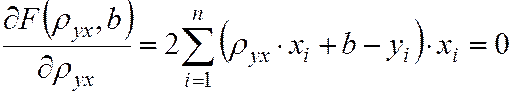
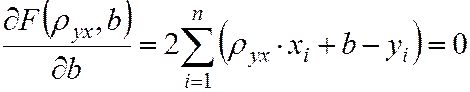
Для отыскания минимума функции приравняем нулю соответствующие частные производные

;

Выполнив преобразования, получим систему

Решив данную систему, найдём искомые параметры

;

. (7.4)

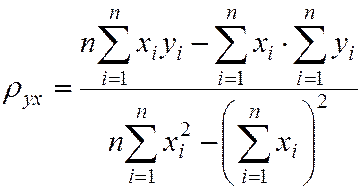
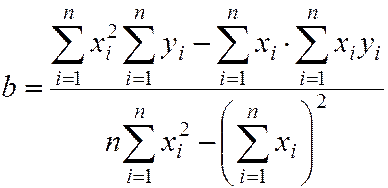
Аналогично можно найти выборочное уравнение прямой линии регрессии X на Y.

. (7.5)

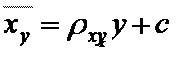
Пример. Найти уравнение прямой линии регрессии по данным наблюдений:

X	1,00	1,50	3,00	4,50	5,00
Y	1,25	1,40	1,50	1,75	2,25

Составляем расчётную таблицу:


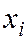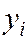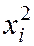1,00	1,25	1,00	1,250
1,50	1,40	2,25	2,100
3,00	1,50	9,00	4,500
4,50	1,75	20,25	4,875
5,00	2,25	25,00	11,250

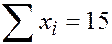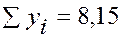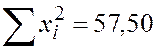Находим неизвестные параметры из уравнения прямой линии регрессии:

;

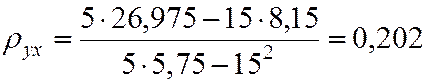
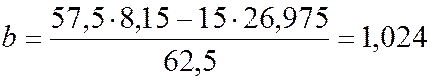
Записываем искомое уравнение:

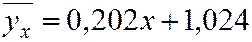
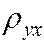
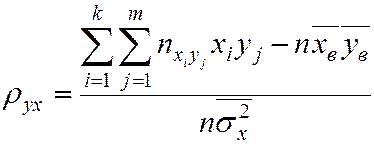
Если данные наблюдений представлены в виде корреляционнной таблицы 6.1, то можно вычислить по формуле

. (7.6)

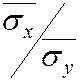
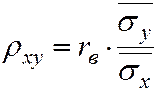
Умножим обе части равенства (7.6) на дробь , получим формулу (6.3) для вычисления r_в.

. (7.7)

Отсюда уравнение (7.3) можно записать через r_в:

. (7.8)

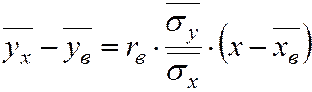
Аналогично уравнение (7.5) примет вид

. (7.9)

Выборочное уравнение нелинейной регрессии

Функции регрессии Y на X могут иметь вид, например, параболической корреляции второго порядка

, (7.10)

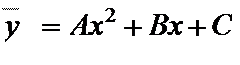
параболической корреляции третьего порядка

где A, B, C, D – неизвествные параметры.

Определить неизвестные параметры можно МНК. Для уравнения (7.9) неизвестные параметры A, B, C находят из решения системы линейных уравнений:

Пример. В. Е. Гмурман «Руководство к решению задач по теории вероятностей и математической статистике», стр. 276.

Элементы дисперсионного анализа

Общие сведения

Дисперсионный анализ применяют, чтобы установить:

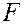
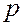
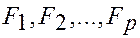
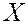
— оказывает ли существенное влияние некоторый качественный фактор , который имеет уровней на изучаемую величину ;

— являются ли однородными несколько совокупностей, т.к. однородные совокупности можно объединить в одну и тем самым получить о ней более полную информацию.

Суть дисперсионного анализасостоит в сравнении «факторной дисперсии» (т.е. межгрупповой), обусловленной воздействием фактора, и «остаточной дисперсии» (т.е. внутригрупповой), порождаемой случайными причинами по критерию Фишера-Снедекора.

Различают дисперсионный анализ:

— однофакторный, если исследуется влияние одного фактора на изучаемую СВ;

— многофакторный, если исследуется воздействие нескольких факторов.

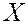
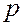
Рассмотрим случай однофакторного дисперсионного анализа, когда на изучаемую величину влияет только один фактор, который имеет постоянных уровней.

Видео:Математика #1 | Корреляция и регрессияСкачать

Задача по эконометрике 3

Задача 3. Определить выборочное уравнение прямой линии регрессии Y на Х по данным корреляционной таблицы. Найти интервал для истинного значения коэффициента корреляции.

Так как данные наблюдений между признаками Х и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то для упрощения вычислений можем перейти к условным вариантам:

где С₁, С₂ – «ложные нули» вариант Х и Y соответственно (новые начала отсчета); h₁, h₂ – шаги (разности между двумя соседними вариантами).

С₁=40; h₁=10;

С₂=15; h₂=5;

Итого

Итого n_u

100

Вычислим групповые средние ū_i и ν_i

Определяем теперь χ и ȳ по формулам:

Вычислим коэффициент корреляции.

При переходе к условным вариантам коэффициент корреляции вычисляется по формуле:

Так как коэффициент корреляции положителен, то делаем вывод о положительной связи между рассматриваемыми признаками, т.е. с увеличением значений признака Х значения признака Y тоже растут.

Найдем уравнение прямой регрессии Y на Х по формуле: