Найти все корни уравнения f x 0 на заданном отрезке a b (7 видео)

Нахождение с заданной точностью корня уравнения F(x)=0 на промежутке [a;b] методом касательных (Ньютона): Отчет по учебно-вычислительной практике

Содержание

Страницы работы
Содержание работы
ОТЧЕТ
Задание
Введение
Найти все корни уравнения f x 0 на заданном отрезке a b
Решение нелинейных уравнений с одной переменной
Тема 1. Решение нелинейных уравнений с одной переменной
🌟 Видео

Страницы работы

Содержание работы

Министерство образования Российской Федерации

Уральский государственный технический университет – УПИ

филиал в г. Краснотурьинске

кафедра вычислительной техники

Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать

ОТЧЕТ

по учебно-вычислительной практике

преподаватель: Мезенцева О.В.

студент: Бурлов А.С.

Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Задание

Тема: «Нахождение с заданной точностью корня уравнения F(x)=0 на промежутке [a;b] методом касательных (Ньютона)»

Контрольный пример: F(x)=0.9x^3-7x^2+5.9x+1.5 на [-1;8]

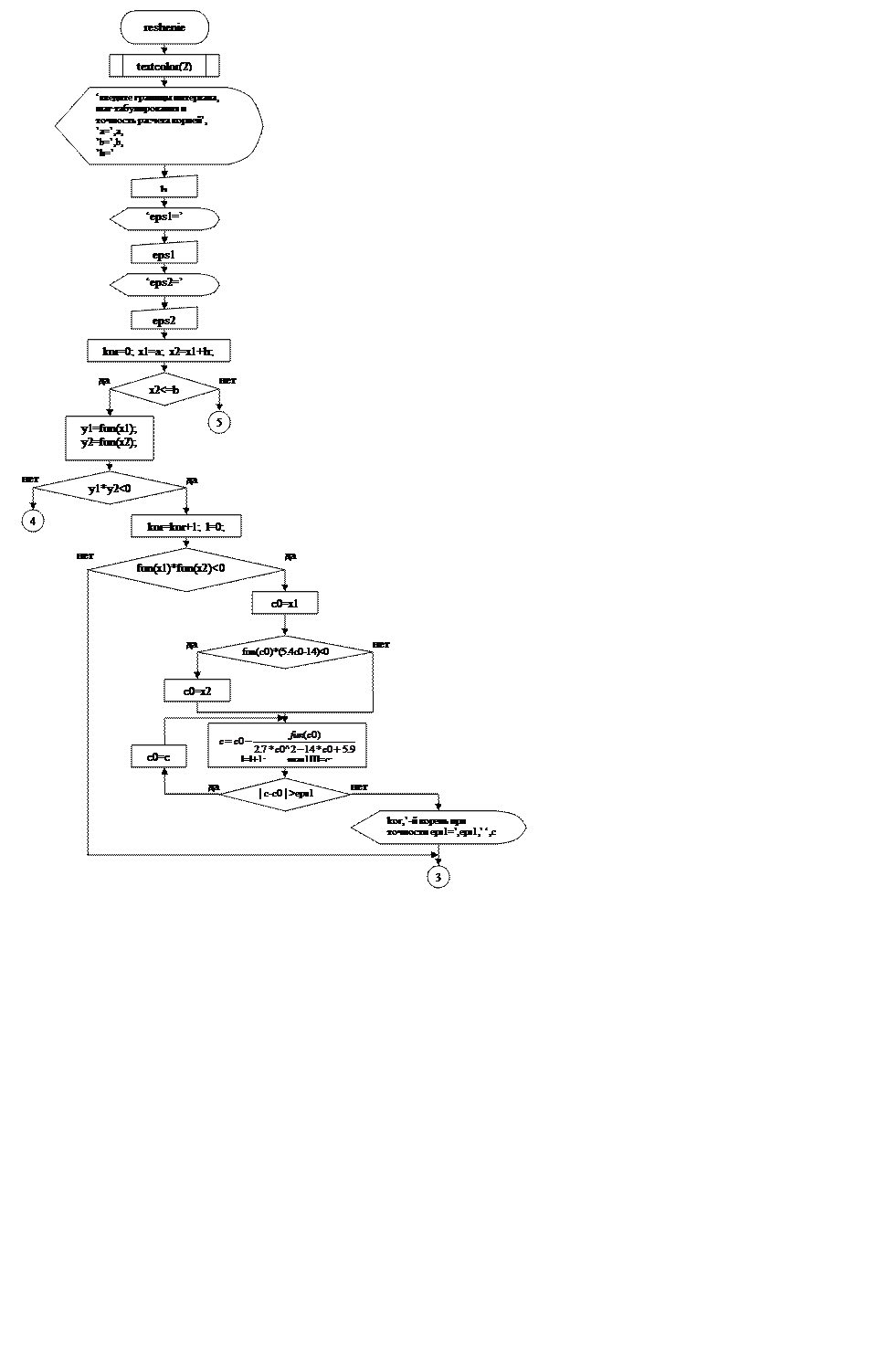
Для данной функции F(x) методом табулирования на интервале [a;b] локализовать корни уравнения F(x)=0 (т.е. выделить по возможности наименьшие отрезки, содержащие по одному корню). Найти эти корни методом касательных. Каждый корень вычислить дважды (с разной точностью). Все приближения к корню записывать в массив, который затем вывести на печать. Предусмотреть построение графика функции на заданном интервале.

2. Описание структуры программы………………………………………………7

3. Входные и выходные данные………………………………………………….12

Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Введение

Цель работы: Изучить метод касательных (Ньютона) и составить программу, которая бы находила с заданной точностью корень F(x)=0.9x^3-7x^2+5.9x+1.5 на промежутке [a;b] методом касательных (Ньютона), а также построить график данной функции.

1. Теоретическая часть

Данный метод используется для локализации корней на заданном интервале и заключается в следующем:

1. Определяются границы интервала [a;b], выбирается шаг изменения аргумента х заданной функции – h;

2. Начальное значение аргумента – левая граница интервала (x₁=h), за следующее значение аргумента – начальное значение плюс шаг (x₂=x₁+h);

4. Проверяется, не превышает ли x₂ правой границы интервала [а;b]; если нет, то вычисляется значение функции от x₂ – y₂(x₂), иначе конец процесса;

5. Проверяются знаки значений функции на границах отрезка [x₁;x₂], если знаки разные, то найденный отрезок содержит корень уравнения иначе нет;

Метод касательных (Ньютона)

В этом способе вместо хорд проводятся касательные и ищут пересечение оси Ох с касательной, проведённой к линии y=f(x) в одной точки А или В.

Выясним, в какой из двух точек А или В надо проводить касательную. Для этого разберём всевозможные варианты знаков f‘(x) и f»(x):

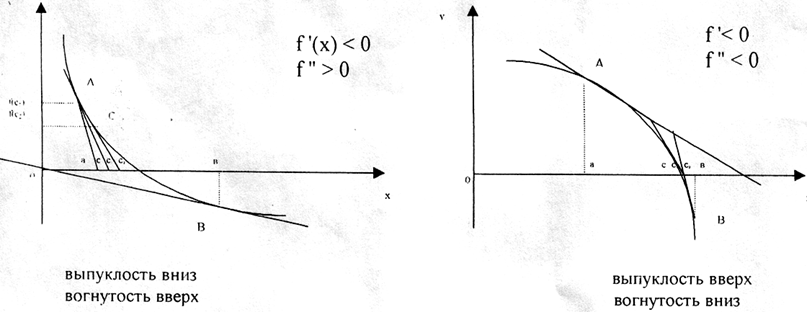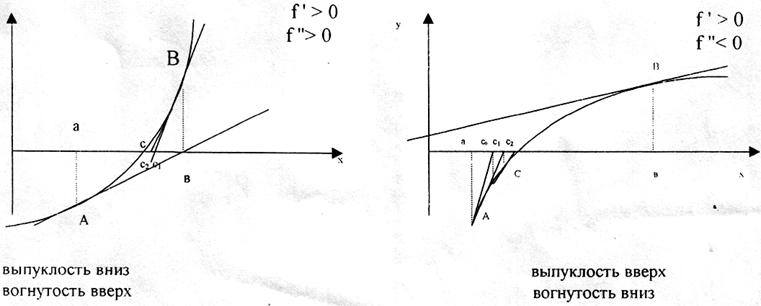Из рисунков видно, что касательную нужно проводить в том из концов дуги АВ, в котором ордината f(x) имеет тот же знак, что и знак второй производной.

– уравнение касательной, проведённой к кривой f(x) в точке с координатами с₀ и f(с₀).

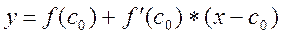
Отсюда найдём следующие приближения корня с₁, как абсциссу точки пересечения касательной с осью Ох (y=0).

Аналогично могут быть найдены и следующие приближения, как точки пересечения с осью абсцисс касательных, проведённых в следующих точках.

Формула для n-го приближения имеет вид:

(f‘(с_n_-1)≠0)

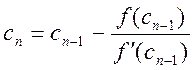
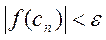
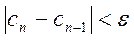
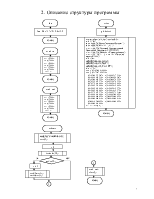
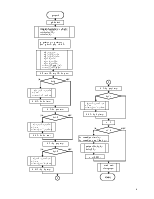
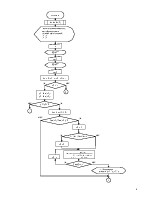
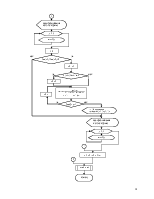
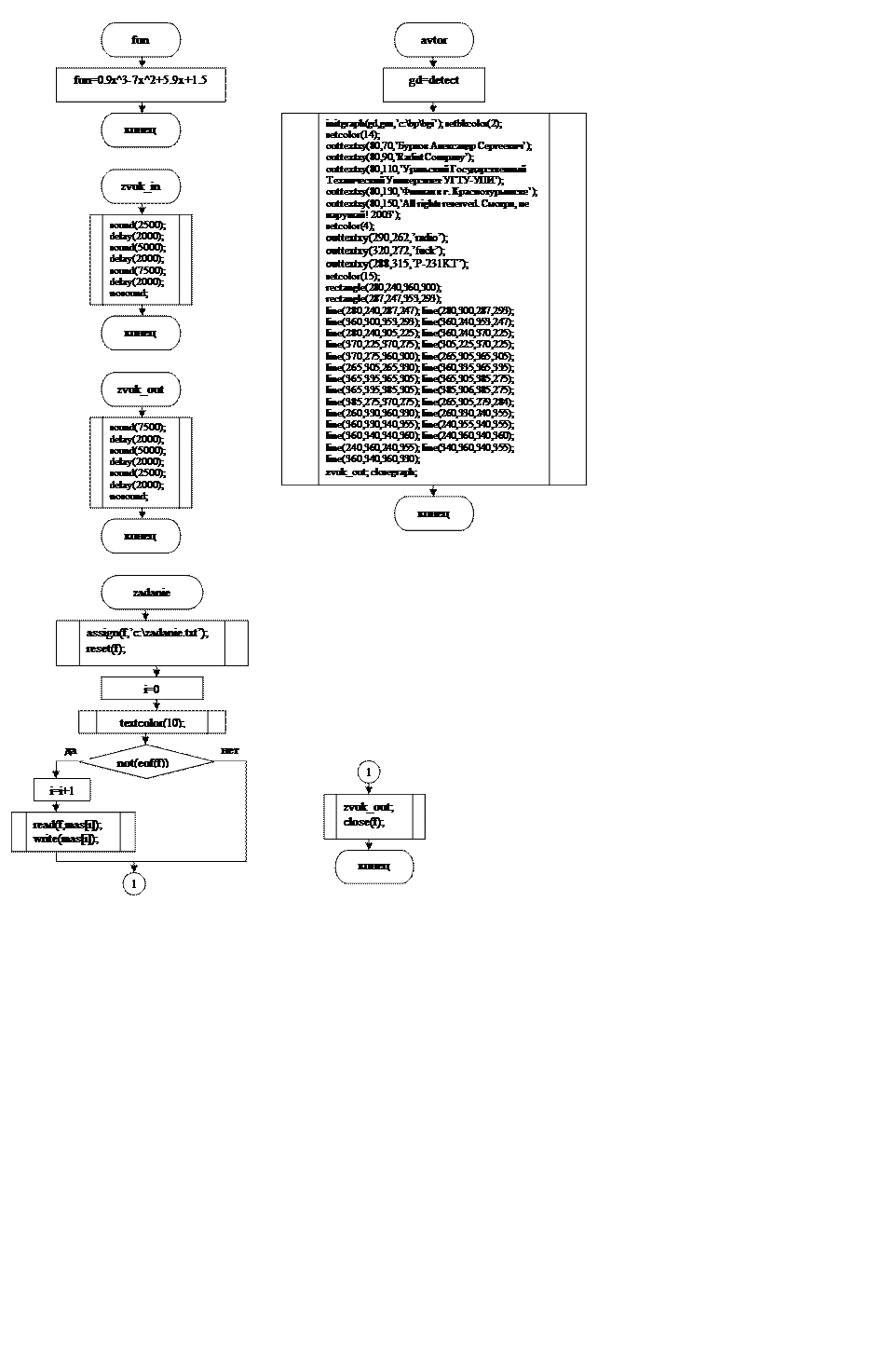
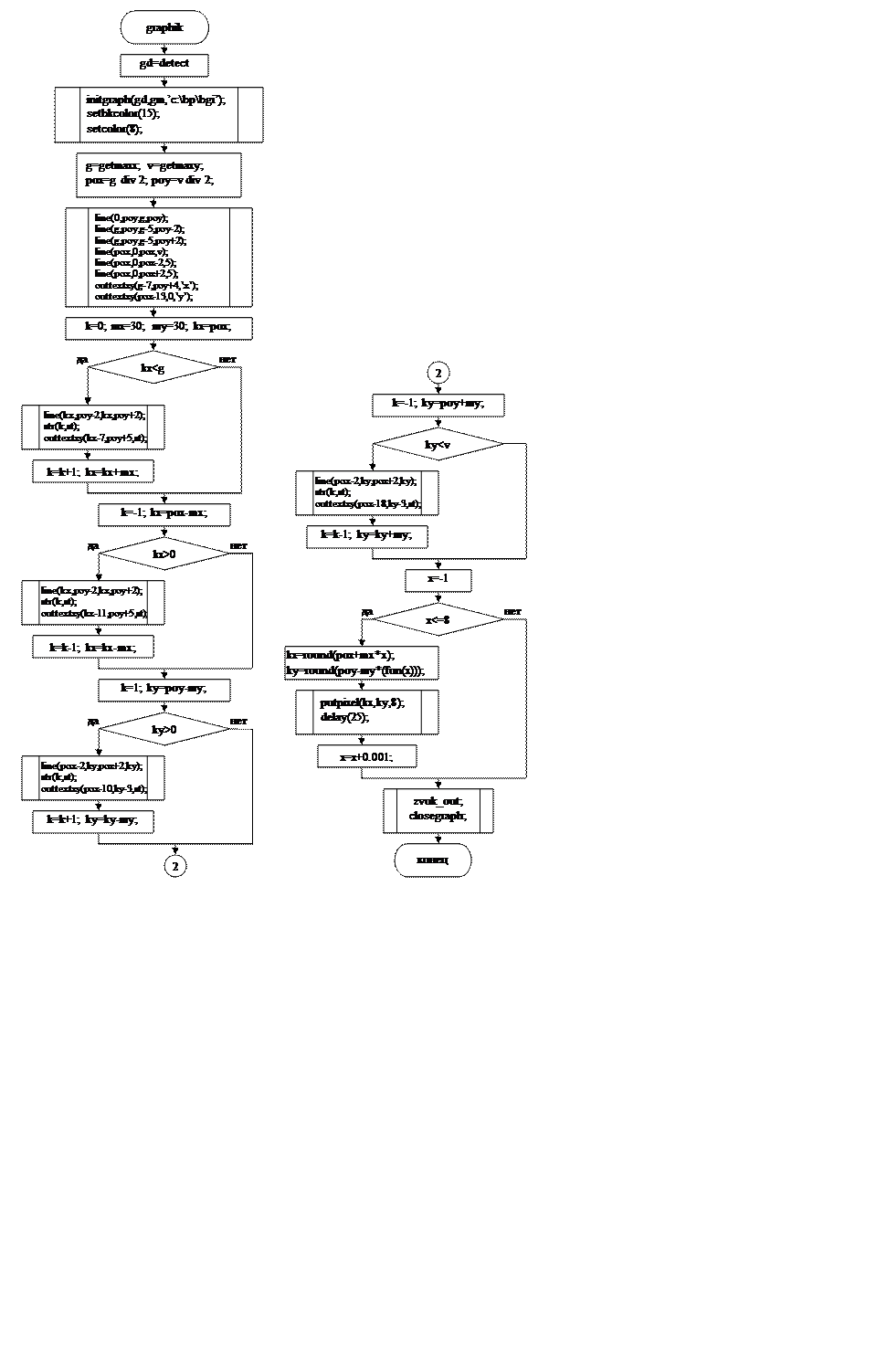
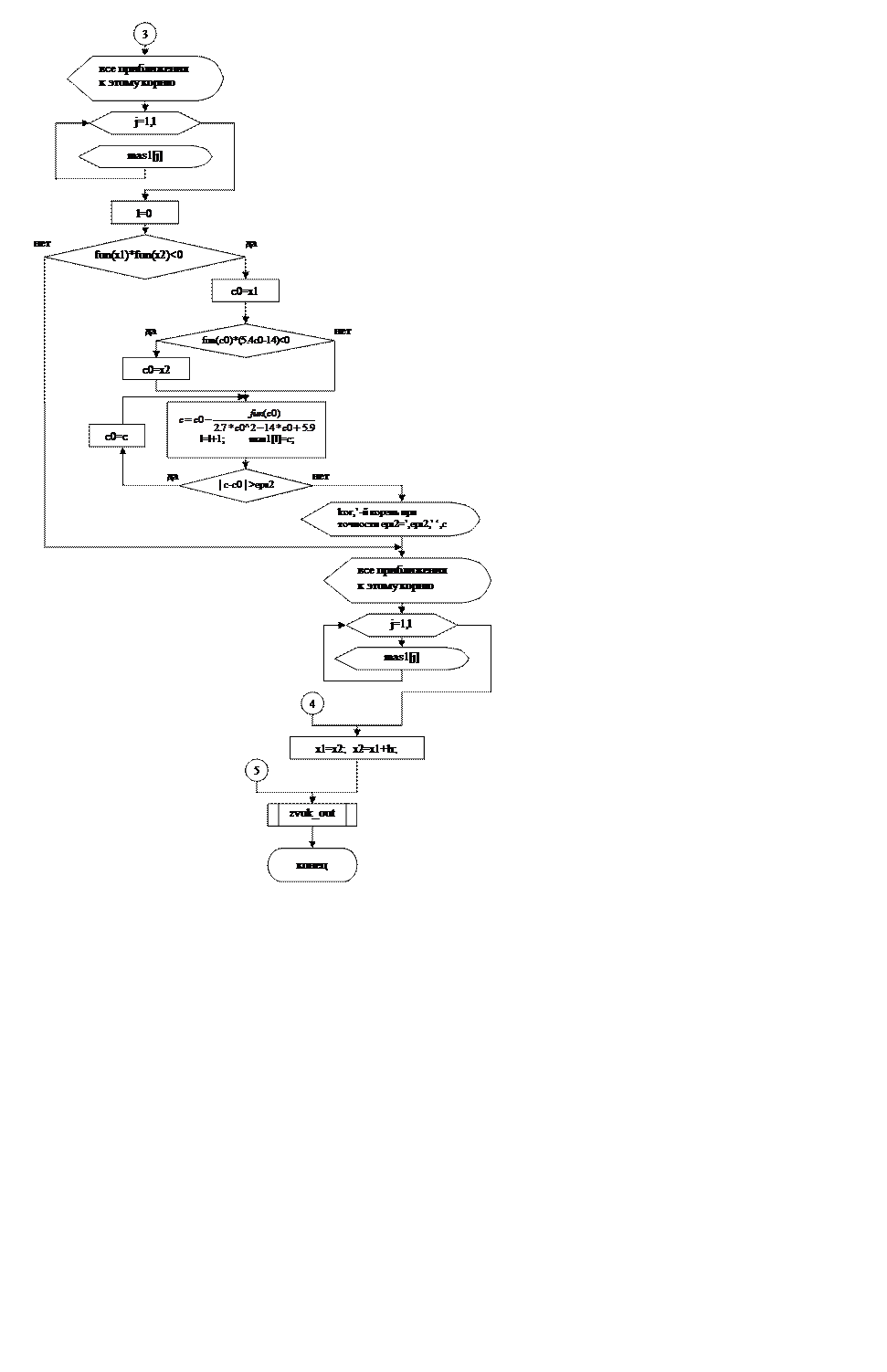
Для окончания итерационного процесса может быть использовано условие или условие близости двух последних приближений: , где с₀, c₁, c_n – приближения значения корня по недостатку.

2. Описание структуры программы

3. Входные и выходные данные

f – файловая переменная

mas – массив из элементов файла

g – максимальное значение по оси Ох

v – максимальное значение по оси Оу

pox – половина максимального значения по оси Ох

poy – половина максимального значения по оси Оу

k – разметка цифрами по осям

mx – масштаб по оси Ох

my – масштаб по оси Оу

kx – число пикселей на единичном отрезке по Ох

ky – число пикселей на единичном отрезке по Оу

st – строковая переменная

x – приращение функции

a, b – границы отрезка

h – шаг табулирования

eps1, eps2 – точности расчета корней

kor – счетчик корней

x1, x2 – границы интервала, который может содержать корень уравнения

y1 – значение функции в точке х1

y2 – значение функции в точке х2

c0 – приближение корня по недостатку

mas1 – массив из приближений к корню

c – корень уравнения

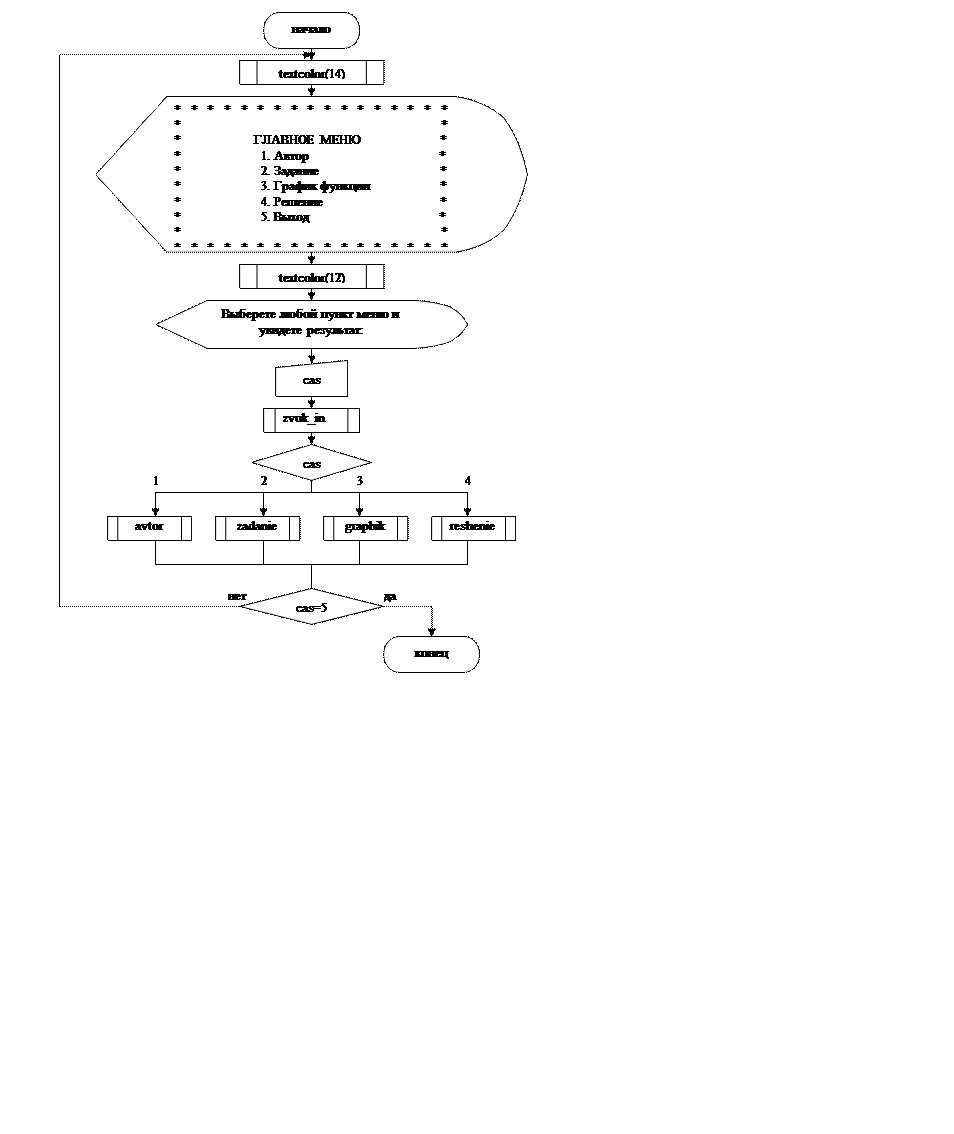
cas — № пункта меню

введите границы интервала, шаг табулирования и точность расчета корней

1-й корень при точности eps1=0.1000 -0.20497419

все приближения к этому корню

1-й корень при точности eps2=0.0100 -0.20371344

все приближения к этому корню

2-й корень при точности eps1=0.1000 1.20786678

все приближения к этому корню

2-й корень при точности eps2=0.0100 1.20786678

все приближения к этому корню

3-й корень при точности eps1=0.1000 6.77372179

все приближения к этому корню

3-й корень при точности eps2=0.0100 6.77365054

все приближения к этому корню

В результате проделанной работы я составил программу, позволяющую на заданном интервале [a,b] локализовать корни уравнения F(x)=0, найти их с заданной точностью методом касательных (Ньютона), построить график функции. Сопоставив результаты, полученные графическим и аналитическим способами, можно заметить, что они практически совпадают.

Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Найти все корни уравнения f x 0 на заданном отрезке a b

Найдем корень нелинейного уравнения в табличном процессоре Excel методом касательных с использованием циклических ссылок. Для нахождения корня будем использовать формулу:

Для включения режима циклических вычислений в Excel 2003 в меню Сервис/Параметры/вкладка Вычисления следует поставить флажок Итерации и флажок выбора вида ведения вычислений: автоматически. В MS Excel 2010 следует зайти в меню Файл/Параметры/Формулы и поставить флажок в поле «Включить итеративные вычисления» :

Найдем производную функции f(x)=x-x 3 +1

f’(x)=1-3x 2
В ячейку А3 введем значение а =1, ячейку В3 введем формулу расчета текущего значения х: =ЕСЛИ(B3=0;A3;B3-(B3-СТЕПЕНЬ(B3;3)+1)/(1-3*СТЕПЕНЬ(B3;2)))
В ячейку С3 введем формулу для контроля значения f(x): =B3-СТЕПЕНЬ(B3;3)+1.
Получим корень уравнения в ячейке В3 х=1,325.

Введем начальное приближение в ячейку А3 =2. Но для того чтобы вычисления были правильные, недостаточно изменить число в ячейке А3 и запустить процесс вычислений. Потому что в этом случае вычисления продолжаться с последнего вычисленного ранее значения. Это значение, в ячейке В3, необходимо обнулить, для этого можно заново записать туда формулу или просто выбрать ячейку с формулой и дважды щелкнуть мышью на ней . После этого поставить курсор на ячейку с формулой и нажать клавишу Enter для запуска процесса итерационных вычислений.

Получим тот же результат, значит корень на данном промежутке один.

Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Решение нелинейных уравнений с одной переменной

Раздел 2. Численные методы

Тема 1. Решение нелинейных уравнений с одной переменной

При решении ряда задач физики, механики и техники возникает необходимость решения уравнений с одной переменной. В общем случае нелинейное уравнение можно записать в виде: F(x)=0, где функция F(x) определена и непрерывна на промежутке . Корнем уравнения F(x)=0, является такое число c из области определения функции y=F(x), для которого справедливо равенство F(c)=0.

Поскольку подавляющее большинство нелинейных уравнений не решается путем аналитических преобразований (точными методами), на практике их решают численными методами. Решить такое уравнение численными методами значит установить, имеет ли оно корни, сколько корней, и найти все его корни с заданной точностью.

Задача численного решения уравнений состоит из двух этапов:

1. Отделение корней, т. е. нахождение достаточно малых окрестностей рассматриваемой области, в которых содержится единственный корень.

2. Уточнение корней, т. е. вычисление корней с заданной степенью точности в некоторой окрестности.

Во многих случаях отделение корней можно произвести графически. Для этого необходимо построить график функции y=F(x) и найти достаточно малые отрезки, содержащие по одной точке пересечения графика с осью ОХ. Иногда построение значительно упрощается, если функцию y=F(x) представить в виде f₁ (x)=f₂ (x) и найти отрезки оси ОХ, содержащие координаты х точек пересечения.

Отделение корней можно также произвести с помощью соответствующей компьютерной программы.

Пусть имеется уравнение F(x)=0, причем все интересующие вычислителя корни находятся на отрезке [A, B], на котором функция определена и непрерывна. Требуется отделить корни уравнения, т.е. найти отрезки [a, b] [A, B], содержащие по одному корню. Очевидно, что если на отрезке [a, b] функция меняет знак, то на этом отрезке находится, по крайней мере, один корень уравнения F(x)=0. Если длина отрезка [a, b] очень мала и F(a)*F(b) 0

Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Данный метод позволяет находить корни уравнения с заданной точностью е. Действительно, если на каком-то этапе процесса деления получен отрезок [a’, b’], содержащий корень, то приняв x≈(a’+b’)/2, мы найдем корень с точностью е (b’-a’)/2.

1.4. Уточнение корней методом итерации

Заменим уравнение F(x)=0 равносильным уравнением x=f(x). Пусть x* — искомый корень уравнения, а x₀ – полученное каким-либо способом грубо приближенное значение корня. Подставим x₀ в правую часть уравнения x=f(x), получим x₁ =f(x₀ ). Продолжая процесс подстановки, получим последовательность чисел: x₂ =f(x₁ ), x₃ =f(x₂ ),…, x_n =f(x_n-1 ). Такая последовательность называется последовательностью приближений или итерационной последовательностью.

Достаточное условие сходимости итерационного процесса

Пусть на отрезке [ a, b] уравнение x= f( x) имеет единственный корень и выполняются условия:

2. [ a, b] для всех х из [ a, b];

3. Существует такое действительное число q, что , для всех х из [ a, b];

Тогда итерационная последовательность x_n = f( x_n-1 ) сходится при любом начальном значении x₀ [ a, b].

Это условие не является необходимым, т.е. итерационная последовательность может сходиться и в том случае, если условия теоремы не выполняются.

Оценка погрешности метода итерации

Пусть , тогда или . Это значит, что процесс итерации надо продолжать до тех пор, пока модуль разности двух соседних приближений не станет меньше .

1.5. Уточнение корней методом хорд

Пусть уравнение F(x)=0 имеет единственный корень на отрезке [a, b]. Если отрезок [a, b] достаточно мал, то можно считать, что функция y=F(x) монотонна на этом отрезке и не меняет направление выпуклости. Значит на отрезке [a, b] нет точек максимума и минимума, т.е. . Т.к. направление выпуклости не меняется то и . Получаем четыре вида графиков, которые объединяются в два типа.

I. тип. Условие: , где x- любая точка [a, b].

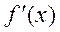
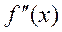
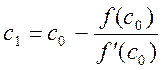
Найти все корни уравнения f x 0 на заданном отрезке a b

II. тип. Условие: , где x- любая точка [a, b].

Пусть x* — искомый корень уравнения F(x)=0. Заменим кривую графика на хорду АВ. Уравнение прямой, проходящей через точки А (а, F(а)) и В(b, F(b)) имеет вид: , где (x, y) – любая точка прямой АВ. В качестве этой точки возмем точку пересечения хорды с осью ОХ, т.е.

(x₁ , 0). Получим или .

Рассмотрим случай, когда кривая графика функции y= F( x) относится к I типу. Через точки А₁ и В проводим следующую хорду. Она пересекает ось ОХ в точке х_2. Аналогично получаем

(1)

Полученная таким образом формула (1) называется формулой метода хорд для кривых I-го типа.

Очевидно, что последовательность значений х₁ , х₂ , х₃ , …,х_n стремится к корню уравнения х * , а значит этот корень можно найти с заданной точностью.