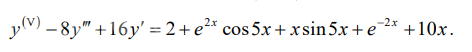Условие
Указать структуру общего решения дифференциального уравнения, не
находя коэффициентов его частных решений. 
Решение
Решаем однородное:
[m]y^-8y«`+16y`=0[/m]
k_(3)=-2 — кратный корень характеристического уравнения, поэтому умножаем на х^2
k_(1)=0 — корень характеристического уравнения, поэтому умножаем на х
y_(частное неод)=Dx^2*e^(-2x) +(Ax+B)*x+e^(2x)*(Mcos5x+Nsin5x)+(Kx+P)*sin5x+(Tx+Q)*cos5x
y_(общее неодн)=y_(общее одн)+y_(частное неод)=.
Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.
Рассмотрим линейное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами вида y » + p · y ‘ + q · y = f ( x ) , где произвольными числами являются p и q , а имеющаяся функция f ( х ) непрерывная на интервале интегрирования x .
Перейдем к формулировке теоремы общего решения ЛНДУ.
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Теорема общего решения ЛДНУ
Общим решением, находящимся на интервале х , неоднородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = f ( x ) с непрерывными коэффициентами интегрирования на x интервале f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функцией f ( x ) равняется сумме общего решения y 0 , которое соответствует ЛОДУ и каким-нибудь частным решением y
, где исходным неоднородным уравнением является y = y 0 + y
Отсюда видно, что решение такого уравнения второго порядка имеет вид y = y 0 + y
. Алгоритм нахождения y 0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y
Выбор частного решения ЛНДУ зависит от вида имеющейся функции f ( x ) , располагающейся в правой части уравнения. Для этого необходимо рассмотреть отдельно решения линейных неоднородных дифференциальных уравнений второго порядка при постоянных коэффициентах.
Когда f ( x ) считается за многочлен n -ой степени f ( x ) = P n ( x ) , отсюда следует, что частное решение ЛНДУ находим по формуле вида y
= Q n ( x ) · x γ , где Q n ( x ) является многочленом степени n , r – это количество нулевых корней характеристического уравнения. Значение y
является частным решением y
= f ( x ) , тогда имеющиеся коэффициенты, которые определены многочленом
Q n ( x ) , отыскиваем при помощи метода неопределенных коэффициентов из равенства y
Вычислить по теореме Коши y » — 2 y ‘ = x 2 + 1 , y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .
Решение
Иначе говоря, необходимо перейти к частному решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами y » — 2 y ‘ = x 2 + 1 , которое будет удовлетворять заданным условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .
Общим решением линейного неоднородного уравнения является сумма общего решения, которое соответствует уравнению y 0 или частному решению неоднородного уравнения y
, то есть y = y 0 + y
Для начала найдем общее решение для ЛНДУ, а после чего – частное.
Перейдем к нахождению y 0 . Запись характеристического уравнения поможет найти корни. Получаем, что
k 2 — 2 k = 0 k ( k — 2 ) = 0 k 1 = 0 , k 2 = 2
Получили, что корни различные и действительные. Поэтому запишем
y 0 = C 1 e 0 x + C 2 e 2 x = C 1 + C 2 e 2 x .
. Видно, что правая часть заданного уравнения является многочленом второй степени, тогда один из корней равняется нулю. Отсюда получим, что частным решением для y
= Q 2 ( x ) · x γ = ( A x 2 + B x + C ) · x = A x 3 + B x 2 + C x , где значения А , В , С принимают неопределенные коэффициенты.
Найдем их из равенства вида y
Тогда получим, что:
‘ = x 2 + 1 ( A x 3 + B x 2 + C x ) » — 2 ( A x 3 + B x 2 + C x ) ‘ = x 2 + 1 3 A x 2 + 2 B x + C ‘ — 6 A x 2 — 4 B x — 2 C = x 2 + 1 6 A x + 2 B — 6 A x 2 — 4 B x — 2 C = x 2 + 1 — 6 A x 2 + x ( 6 A — 4 B ) + 2 B — 2 C = x 2 + 1
Приравняв коэффициенты с одинаковыми показателями степеней x , получим систему линейных выражений — 6 A = 1 6 A — 4 B = 0 2 B — 2 C = 1 . При решении любым из способов найдем коэффициенты и запишем: A = — 1 6 , B = — 1 4 , C = — 3 4 и y
= A x 3 + B x 2 + C x = — 1 6 x 3 — 1 4 x 2 — 3 4 x .
Эта запись называется общим решением исходного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Для нахождения частного решения, которое удовлетворяет условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 , требуется определить значения C 1 и C 2 , исходя из равенства вида y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .
y ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x x = 0 = C 1 + C 2 y ‘ ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x ‘ x = 0 = = 2 C 2 e 2 x — 1 2 x 2 + 1 2 x + 3 4 x = 0 = 2 C 2 — 3 4
Работаем с полученной системой уравнений вида C 1 + C 2 = 2 2 C 2 — 3 4 = 1 4 , где C 1 = 3 2 , C 2 = 1 2 .
Применив теорему Коши, имеем, что
y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x = = 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x
Ответ: 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .
Когда функция f ( x ) представляется в виде произведения многочлена со степенью n и экспоненты f ( x ) = P n ( x ) · e a x , тогда отсюда получаем, что частным решением ЛНДУ второго порядка будет уравнение вида y
= e a x · Q n ( x ) · x γ , где Q n ( x ) является многочленом n -ой степени, а r – количеством корней характеристического уравнения, равняющиеся α .
Коэффициенты, принадлежащие Q n ( x ) находятся по равенству y
Найти общее решение дифференциального уравнения вида y » — 2 y ‘ = ( x 2 + 1 ) · e x .
Решение
Уравнение общего вида y = y 0 + y
. Указанное уравнение соответствует ЛОДУ y » — 2 y ‘ = 0 . По предыдущему примеру видно, что его корни равняются k 1 = 0 и k 2 = 2 и y 0 = C 1 + C 2 e 2 x по характеристическому уравнению.
Видно, что правой частью уравнения является x 2 + 1 · e x . Отсюда ЛНДУ находится через y
= e a x · Q n ( x ) · x γ , где Q n ( x ) , являющимся многочленом второй степени, где α = 1 и r = 0 , потому как у характеристического уравнения отсутствует корень, равный 1 . Отсюда получаем, что
= e a x · Q n ( x ) · x γ = e x · A x 2 + B x + C · x 0 = e x · A x 2 + B x + C .
А , В , С являются неизвестными коэффициентами, которые можно найти по равенству y
‘ = e x · A x 2 + B x + C ‘ = e x · A x 2 + B x + C + e x · 2 A x + B = = e x · A x 2 + x 2 A + B + B + C y
‘ ‘ = e x · A x 2 + x 2 A + B + B + C ‘ = = e x · A x 2 + x 2 A + B + B + C + e x · 2 A x + 2 A + B = = e x · A x 2 + x 4 A + B + 2 A + 2 B + C
‘ = ( x 2 + 1 ) · e x ⇔ e x · A x 2 + x 4 A + B + 2 A + 2 B + C — — 2 e x · A x 2 + x 2 A + B + B + C = x 2 + 1 · e x ⇔ e x · — A x 2 — B x + 2 A — C = ( x 2 + 1 ) · e x ⇔ — A x 2 — B x + 2 A — C = x 2 + 1 ⇔ — A x 2 — B x + 2 A — C = 1 · x 2 + 0 · x + 1
Показатели при одинаковых коэффициентах приравниваем и получаем систему линейных уравнений. Отсюда и находим А , В , С :
— A = 1 — B = 0 2 A — C = 1 ⇔ A = — 1 B = 0 C = — 3
Ответ: видно, что y
= e x · ( A x 2 + B x + C ) = e x · — x 2 + 0 · x — 3 = — e x · x 2 + 3 является частным решением ЛНДУ, а y = y 0 + y = C 1 e 2 x — e x · x 2 + 3 — общим решением для неоднородного дифуравнения второго порядка.
Когда функция записывается как f ( x ) = A 1 cos ( β x ) + B 1 sin β x , а А 1 и В 1 являются числами, тогда частным решением ЛНДУ считается уравнение вида y
= A cos β x + B sin β x · x γ , где А и В считаются неопределенными коэффициентами, а r числом комплексно сопряженных корней, относящихся к характеристическому уравнению, равняющимся ± i β . В этом случае поиск коэффициентов проводится по равенству y
Найти общее решение дифференциального уравнения вида y » + 4 y = cos ( 2 x ) + 3 sin ( 2 x ) .
Решение
Перед написанием характеристического уравнения находим y 0 . Тогда
k 2 + 4 = 0 k 2 = — 4 k 1 = 2 i , k 2 = — 2 i
Имеем пару комплексно сопряженных корней. Преобразуем и получим:
y 0 = e 0 · ( C 1 cos ( 2 x ) + C 2 sin ( 2 x ) ) = C 1 cos 2 x + C 2 sin ( 2 x )
Корни из характеристического уравнения считаются сопряженной парой ± 2 i , тогда f ( x ) = cos ( 2 x ) + 3 sin ( 2 x ) . Отсюда видно, что поиск y
будет производиться из y
= ( A cos ( β x ) + B sin ( β x ) · x γ = ( A cos ( 2 x ) + B sin ( 2 x ) ) · x . Неизвестные коэффициенты А и В будем искать из равенства вида y
= cos ( 2 x ) + 3 sin ( 2 x ) .
‘ = ( ( A cos ( 2 x ) + B sin ( 2 x ) · x ) ‘ = = ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) y
» = ( ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) ) ‘ = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) — — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x )
Тогда видно, что
= cos ( 2 x ) + 3 sin ( 2 x ) ⇔ ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) + + 4 ( A cos ( 2 x ) + B sin ( 2 x ) ) · x = cos ( 2 x ) + 3 sin ( 2 x ) ⇔ — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) = cos ( 2 x ) + 3 sin ( 2 x )
Необходимо приравнять коэффициенты синусов и косинусов. Получаем систему вида:
— 4 A = 3 4 B = 1 ⇔ A = — 3 4 B = 1 4
= ( A cos ( 2 x ) + B sin ( 2 x ) · x = — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x .
Ответ: общим решением исходного ЛНДУ второго порядка с постоянными коэффициентами считается
= = C 1 cos ( 2 x ) + C 2 sin ( 2 x ) + — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x
Когда f ( x ) = e a x · P n ( x ) sin ( β x ) + Q k ( x ) cos ( β x ) , тогда y
= e a x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ . Имеем, что r – это число комплексно сопряженных пар корней, относящихся к характеристическому уравнению, равняются α ± i β , где P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , т , m , где m = m a x ( n , k ) . Нахождение коэффициентов L m ( x ) и N m ( x ) производится, исходя из равенства y
Найти общее решение y » + 3 y ‘ + 2 y = — e 3 x · ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) .
Решение
По условию видно, что
α = 3 , β = 5 , P n ( x ) = — 38 x — 45 , Q k ( x ) = — 8 x + 5 , n = 1 , k = 1
Тогда m = m a x ( n , k ) = 1 . Производим нахождение y 0 , предварительно записав характеристическое уравнение вида:
k 2 — 3 k + 2 = 0 D = 3 2 — 4 · 1 · 2 = 1 k 1 = 3 — 1 2 = 1 , k 2 = 3 + 1 2 = 2
Получили, что корни являются действительными и различными. Отсюда y 0 = C 1 e x + C 2 e 2 x . Далее необходимо искать общее решение, исходя из неоднородного уравнения y
= e α x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) · x 0 = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) )
Известно, что А , В , С являются коэффициентами, r = 0 , потому как отсутствует пара сопряженных корней, относящихся к характеристическому уравнению с α ± i β = 3 ± 5 · i . Данные коэффициенты находим из полученного равенства:
= — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) ⇔ ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) » — — 3 ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) = — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) )
Нахождение производной и подобных слагаемых дает
— e 3 x · ( ( 15 A + 23 C ) · x · sin ( 5 x ) + + ( 10 A + 15 B — 3 C + 23 D ) · sin ( 5 x ) + + ( 23 A — 15 C ) · x · cos ( 5 x ) + ( — 3 A + 23 B — 10 C — 15 D ) · cos ( 5 x ) ) = = — e 3 x · ( 38 · x · sin ( 5 x ) + 45 · sin ( 5 x ) + + 8 · x · cos ( 5 x ) — 5 · cos ( 5 x ) )
После приравнивания коэффициентов получаем систему вида
15 A + 23 C = 38 10 A + 15 B — 3 C + 23 D = 45 23 A — 15 C = 8 — 3 A + 23 B — 10 C — 15 D = — 5 ⇔ A = 1 B = 1 C = 1 D = 1
Из всего следует, что
= e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) = = e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )
Ответ: теперь получено общее решение заданного линейного уравнения:
= = C 1 e x + C 2 e 2 x + e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )
Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать
Алгоритм решения ЛДНУ
Любой другой вид функции f ( x ) для решения предусматривает соблюдение алгоритма решения:
- нахождение общего решения соответствующего линейного однородного уравнения, где y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 являются линейно независимыми частными решениями ЛОДУ, С 1 и С 2 считаются произвольными постоянными;
- принятие в качестве общего решения ЛНДУ y = C 1 ( x ) ⋅ y 1 + C 2 ( x ) ⋅ y 2 ;
- определение производных функции через систему вида C 1 ‘ ( x ) + y 1 ( x ) + C 2 ‘ ( x ) · y 2 ( x ) = 0 C 1 ‘ ( x ) + y 1 ‘ ( x ) + C 2 ‘ ( x ) · y 2 ‘ ( x ) = f ( x ) , а нахождение функций C 1 ( x ) и C 2 ( x ) посредствам интегрирования.
Найти общее решение для y » + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x .
Решение
Переходим к написанию характеристического уравнения, предварительно записав y 0 , y » + 36 y = 0 . Запишем и решим:
k 2 + 36 = 0 k 1 = 6 i , k 2 = — 6 i ⇒ y 0 = C 1 cos ( 6 x ) + C 2 sin ( 6 x ) ⇒ y 1 ( x ) = cos ( 6 x ) , y 2 ( x ) = sin ( 6 x )
Имеем, что запись общего решения заданного уравнения получит вид y = C 1 ( x ) · cos ( 6 x ) + C 2 ( x ) · sin ( 6 x ) . Необходимо перейти к определению производных функций C 1 ( x ) и C 2 ( x ) по системе с уравнениями:
C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) · ( cos ( 6 x ) ) ‘ + C 2 ‘ ( x ) · ( sin ( 6 x ) ) ‘ = 0 ⇔ C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) ( — 6 sin ( 6 x ) + C 2 ‘ ( x ) ( 6 cos ( 6 x ) ) = = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x
Необходимо произвести решение относительно C 1 ‘ ( x ) и C 2 ‘ ( x ) при помощи любого способа. Тогда запишем:
C 1 ‘ ( x ) = — 4 sin 2 ( 6 x ) + 2 sin ( 6 x ) cos ( 6 x ) — 6 e 6 x sin ( 6 x ) C 2 ‘ ( x ) = 4 sin ( 6 x ) cos ( 6 x ) — 2 cos 2 ( 6 x ) + 6 e 6 x cos ( 6 x )
Каждое из уравнений следует проинтегрировать . Тогда запишем получившиеся уравнения:
C 1 ( x ) = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 C 2 ( x ) = — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4
Отсюда следует, что общее решение будет иметь вид:
y = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 · cos ( 6 x ) + + — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4 · sin ( 6 x ) = = — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )
Ответ: y = y 0 + y
= — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )
📺 Видео
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать
15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать
18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать
Видеоурок "Нахождение частных решений по виду правой части"Скачать
19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
13. Как решить дифференциальное уравнение первого порядка?Скачать
Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать
Математика без Ху!ни. Метод неопределенных коэффициентов.Скачать
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
7. ДУ. ЛНДУ с правой частью спец вида (4270 Берман Г.Н)Скачать
17. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами Ч2Скачать
Метод неопределенных коэффициентовСкачать
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать
