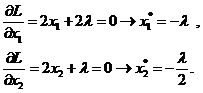Найти условный экстремум функции при заданном уравнении связи онлайн калькулятор (6 видео)

Содержание

Функция Лагранжа
Правило множителей Лагранжа
Условные экстремумы и функция Лагранжа
Экстремумы функции онлайн
🎬 Видео

Видео:Найти условный экстремум функции двух переменных. Одно уравнение связи.Скачать

Функция Лагранжа

Назначение сервиса . Онлайн-калькулятор используется для нахождения экстремума функции через множители Лагранжа в онлайн режиме (см. пример и пример решения графическим способом). При этом решаются следующие задачи:

составляется функция Лагранжа L(X) в виде линейной комбинации функции F(X) и ограничений g_i(x);
находятся частные производные функции Лагранжа, ∂L/∂x_i, ∂L/∂λ_i;
составляется система из (n + m) уравнений, ∂L/∂x_i = 0.
определяются переменные x_i и множители Лагранжа λ_i.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Метод множителей Лагранжа применяется как в линейном программировании, так и в нелинейном. В экономике этот метод используется в задаче потребительского выбора.

Видео:Нахождение условного экстремума функции двух переменных. Метод Лагранжа.Скачать

Правило множителей Лагранжа

Пример 1 . Методом множителей Лагранжа решить следующую задачу оптимизации:
min f(x) = x₁ 2 + x₂ 2
h₁(x) = 2x₁ + x₂ -2 = 0
Соответствующая задача оптимизации без ограничений записывается в следующем виде:
L(x, λ) = x₁ 2 + x₂ 2 + λ(2x₁ + x₂ – 2) → min
Решение:

Для того чтобы проверить, соответствует ли стационарная точка X минимуму, вычислим матрицу Гессе функции L(x, λ), рассматриваемой как функция от x,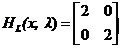
,
которая оказывается положительно определенной (2*2 – 0*0 = 4 > 0).
Это означает, что L(x, λ) – выпуклая функция. Следовательно, координаты x * = (-λ, λ/2) определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x₁ * и x₂ * в уравнение ограничений 2x₁ + x₂ -2 = 0, откуда вычисляем значение λ:
2λ + λ/2 = -2, откуда λ = -0.8
Таким образом, минимум достигается в точке x * с координатами x₁ * = 0.8 и x₂ * = 0.4. Значение ЦФ:
min f(x) = 0.8
Ответ: x * = [0.8; 0.4] T , f(x * ) = 0.8

Пример 2 . Исследовать на условный экстремум функцию f(x,y)_max = x 2 + 8xy+3y 2 при данных уравнениях связи.
9x +10y = 29

Видео:Условный экстремум и функция ЛагранжаСкачать

Условные экстремумы и функция Лагранжа

В задачах оптимизации возникает необходимость найти экстремумы функции двух и более переменных при условии, что существует связь между переменными этой связи, заданная уравнением . В этом случае говорят, что требуется найти условный экстремум.

Для того чтобы найти условный экстремум требуется находить частные производные и решать системы уравнений Существует алгоритм нахождения условного экстремума из трёх шагов, который сейчас и разберём на примере, и геометрический смысл условного экстремума, который должен дойти до каждого при разборе этого самого примера.

Итак, алгоритм, который разберём на примере самой распространённой задачи — нахождение условного экстремума функции двух переменных..

Шаг 1. Вводится функция Лагранжа

где первое слагаемое — сама исходная функция, а второе слагаемое со знаком минус — левая часть уравнения условия связи, умноженная на (лямбда) — множитель Лагранжа.

Пример 1. Найти условные экстремумы функции двух переменных , выражающей площадь прямоугольника через его стороны x и y при условии , означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.

Шаг 1. Решение. Приведём уравнение условия связи к требуемому виду с нулём в правой части:

Составим функцию Лагранжа:

Шаг 2. Составляем систему уравнений из равенств частных производных нулю и уравения условия связи (необходимый признак существования условного экстремума):

Решения этой системы уравнений являются точками возможного условного экстремума — стационарными точками или, как ещё говорят, критическими точками.

Решение. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:

Получили и . Эти значения являются также координатами стационарной точки. Таким образом, получили стационарную точку .

Шаг 3. Пусть является стационарной точкой, найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно найти второй дифференциал функции Лагранжа

и в полученном выражении подставить вместо «лямбды» её значения (значения множителя Лагранжа), найденные на шаге 2.

Если значение второго дифференциала функции Лагранжа меньше нуля (), то стационарная точка является точкой максимума, если больше нуля (), то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в задачах, задаваемых студентам.

Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).

Решение. Найдём второй дифференциал функции Лагранжа:

В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy :

Так как полученные значения — противоположные по знаку, то получаем, что в любом случае .

Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:

Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.

Пример 2. Найти условные экстремумы функции двух переменных при условии .

Шаг 1. Составим функцию Лагранжа:

Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y :

Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:

Эти значения икса и игрека являются координатами двух стационарных точек. Таким образом, получили стационарные точки .

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

Найдём второй дифференциал функции Лагранжа по формуле

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точка — точка условного максимума:

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точка — точка условного минимума:

Таким образом, условные экстремумы заданной функции найдены.

Пример 3. Найти условные экстремумы функции двух переменных при условии .

Шаг 1. Составим функцию Лагранжа:

Из первого и второго уравнений выразим соответственно x и y :

Получаем, что , однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому считаем, что на самом деле второй сомножитель равенства равен нулю: . Отсюда получаем

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что . Из третьего уравнения системы получаем:

Получили две стационарные точки:

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что .

На основании вычислений двух первых стационарных точек получилаем ещё две стационарные точки:

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

Найдём второй дифференциал функции Лагранжа по формуле

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точки — точки условного максимума:

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точки — точки условного минимума:

Таким образом, условные экстремумы заданной функции найдены.

Аналогичным образом можно находить условные экстремумы функций трёх и более переменных.

Видео:Математика без Ху!ни. Экстремум функции 2х переменных.Скачать

Экстремумы функции онлайн

Экстремумом функции называется точка минимума или максимума функции. Рассмотрим функцию, график которой приведен на рисунке:

Из графика видно, что точки ( x ₁ , y ₁ ) , ( x ₃ , y ₃ ) являются точками максимума функции, точки ( x ₂ , y ₂ ) , ( x ₄ , y ₄ ) — точками минимума функции. Вместе эти точки, называются точками экстремума функции.

Характерной особенностью является тот факт, что касательная к функции в точках экстремума параллельна оси абсцисс (геометрический смысл точек экстремума). Отсюда немедленно следует, что производная функции в точках экстремума равна нулю (необходимое условие экстремума). Кроме того, в точках экстремума функция может быть не дифференцируемой.

Иногда, требуется найти минимальное (максимальное) значение функции на некотором интервале [ a , b ] . В этом случае необходимо найти точки экстремума функции принадлежащие этому интервалу, а также проверить значения функции на концах интервала.