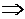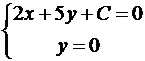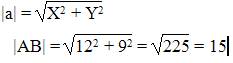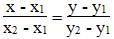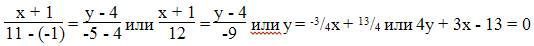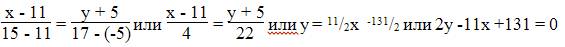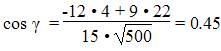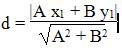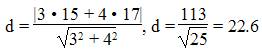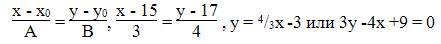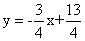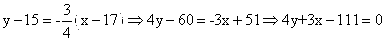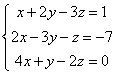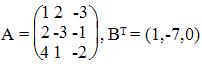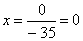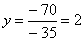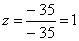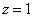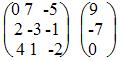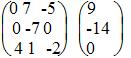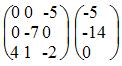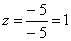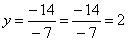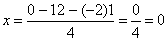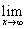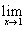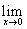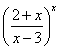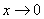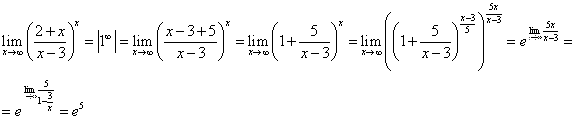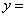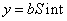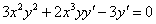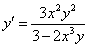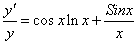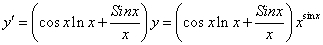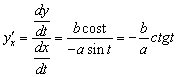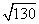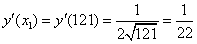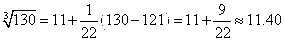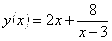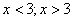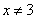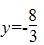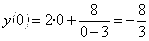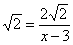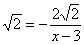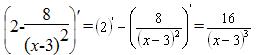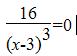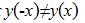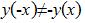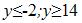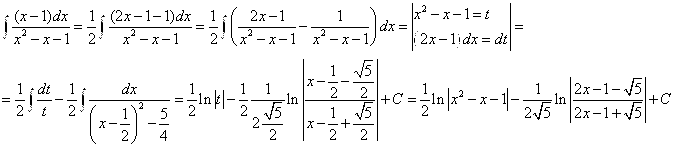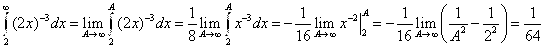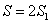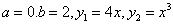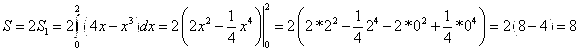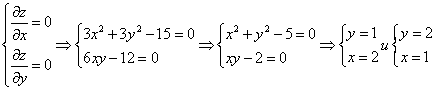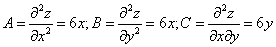Альтернативная формула:
Прямая, проходящая через точку M1(x1; y1) и параллельная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).
Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника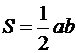 
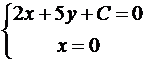
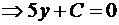
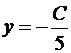
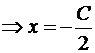
, где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: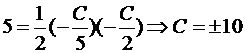 
. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .
Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /7x – 4 /7 (здесь a = 5 /7). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .
Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.
Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).
Видео:Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать
Найти уравнения прямой проходящей через точку a параллельно вс
Даны точки А(1;2), В(6;2), С(3;0).
a) уравнение и длину BC;
Вектор ВС = (3-6; 0 -2) = (-3; -2). Модуль равен √((-3)² + (-2)²) = √13.
Уравнение ВС: (х — 6)/(-3) = (у — 2)/(-2).
или в общем виде 2х — 3у — 6 = 0.
б) уравнение высоты АД;
Высота АД перпендикулярна стороне ВС: 2х — 3у — 6 = 0.
Её уравнение имеет вид 3х + 2у + С = 0 (коэффициенты А и В из уравнение стороны АВ меняются на -В и А).
Для определения величины С подставим координаты точки А(1;2).
АД: 3*1 + 2*2 + С = 0, отсюда С = -3 — 4 = -7.
АД: 3х + 2у — 7 = 0.
в) уравнение прямой, проходящей через точку А параллельно ВС;
Коэфициенты А и В сохраняются такими же, как и у стороны ВС.
2х — 3у + С = 0, для определения параметра С подставим координаты точки А(1;2): 2*1 – 3*2 + С = 0, отсюда С = -2 + 6 = 4.
Уравнение 2х — 3у + 4 = 0.
г) уравнение прямой, соединяющей середины сторон АВ и ВС.
Это будет средняя линия треугольника, параллельная стороне АС.
Находим координаты точки Д, являющейся серединой стороны АВ.
Д = (А(1;2) + В(6;2))/2 = (3,5; 2).
Коэфициенты А и В сохраняются такими же, как и у стороны АС.
Точки А(1;2) и С(3;0).
Вектор АС = (3-1; 0-2) = (2; -2).
Уравнение АС: (х — 1)/2 = (у — 2)/(-2) или в общем виде
Тогда параллельная прямая имеет вид x + y + С = 0.
Для определения параметра С подставим координаты точки Д(3,5; 2):
1*3,5 + 1*2 + С = 0, отсюда С = -3,5 — 2 = -5,5.
Уравнение х + у – 5,5 = 0 или в целых числах 2x + 2y – 11 = 0.
д) угол А треугольника АВС.
Вектор АВ = (6-1; 2-2) = (4; 0), модуль равен 4.
Вектор АС = (2; -2 ), модуль равен √8 = 2√2.
cos B = (4*2 + 0*(-2)) / (4*2√2) = 8 / (8*√2) = 1/√2 = √2/2.
B = arc cos(√2/2) = 45 градусов.
Видео:12. Уравнения прямой в пространстве Решение задачСкачать
Элементы линейной алгебры и аналитической геометрии, графики, матрицы, пределы, мнк
Элементы линейной алгебры и аналитической геометрии
Задания 1-10. Даны координаты точек: А(х1;у1), В(х2;у2), С(х3;у3).
Значения координат точек приведены в таблице к этому заданию.
А) длину отрезка АВ;
Б) уравнение прямых АВ и ВС, проведенных через точки А, В и В, С соответственно;
В) угол θ между прямыми АВ и ВС;
Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;
Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;
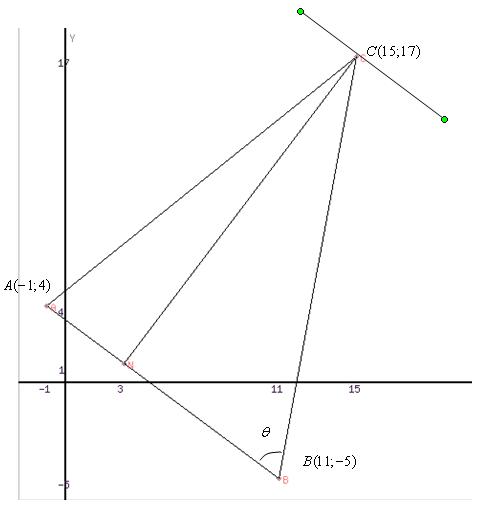
Е) построить чертеж, на котором показать заданные точки, угол θ и прямые.
Координаты векторов находим по формуле: X = xj — xi; Y = yj — yi
Здесь X, Y координаты вектора; xi, yi — координаты точки Аi; xj, yj — координаты точки Аj
Для вектора AB X = x2 — x1; Y = y2 — y1
X = 11—1 = 12; Y = -5-4 = -9
А) длина отрезка АВ
Длина вектора a(X;Y) выражается через его координаты формулой:
Б) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
Уравнение прямой AB
Каноническое уравнение прямой:
Уравнение прямой BC
Каноническое уравнение прямой:
В) угол θ между прямыми АВ и ВС;
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле: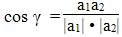 
где a1a2 = X1X2 + Y1Y2
Найдем угол между сторонами BA и BC
γ = arccos(0.45) = 63.440
Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;
Длина высоты треугольника, проведенной из вершины C
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины: 
Найдем расстояние между точкой C(15;17) и прямой AB (4y + 3x — 13 = 0)
Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой
Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Найдем точку пересечения с прямой AB:
Имеем систему из двух уравнений:
Из первого уравнения выражаем y и подставим во второе уравнение.
Получаем: x = 3, y = 1
Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;
Уравнение прямой, проходящей через данную точку С(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y — y1 = k(x — x1).
Это уравнение определяет пучок прямых, проходящих через точку С(x1, y1), которая называется центром пучка. А k — это коэффициент при х уравнения прямой АВ 
Тогда получим 
Е) построим чертеж
Задания 11-20. Решить систему уравнений двумя способами (по формулам Крамера и методом Гаусса)
№12. 
По формулам Крамера.
Запишем систему в виде:
∆ = 1 • (-3 • (-2)-1 • (-1))-2 • (2 • (-2)-1 • (-3))+4 • (2 • (-1)-(-3 • (-3))) = -35 = -35
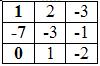
Заменим 1-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
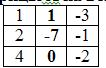
∆1 = 1 • (-3 • (-2)-1 • (-1))-(-7 • (2 • (-2)-1 • (-3)))+0 • (2 • (-1)-(-3 • (-3))) = 0
Заменим 2-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
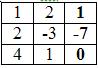
∆2 = 1 • (-7 • (-2)-0 • (-1))-2 • (1 • (-2)-0 • (-3))+4 • (1 • (-1)-(-7 • (-3))) = -70
Заменим 3-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆3 = 1 • (-3 • 0-1 • (-7))-2 • (2 • 0-1 • 1)+4 • (2 • (-7)-(-3 • 1)) = -35
Выпишем отдельно найденные переменные: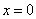 
, 
, 
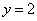
Запишем систему в виде расширенной матрицы: 
Умножим 1-ую строку на (2). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой: 
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой: 
Добавим 2-ую строку к 1-ой: 
Теперь исходную систему можно записать как:
Из 1-ой строки выражаем z: 
Из 2-ой строки выражаем у: 
Из 3-ой строки выражаем x: 
Введение в математический анализ.
Производная и ее приложения.
Задания 21-30. Найти указанные пределы, не пользуясь правилом Лопиталя:
№22. а)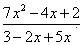 
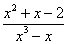
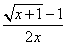
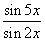
;б) 
;в)
;г)
;д)
А) 
;
Б) 
;
В) 
;
Г)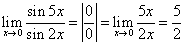 
;
Использовали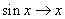 
при 
Д) 
Задания 31-40. Задана функция y=ƒ(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
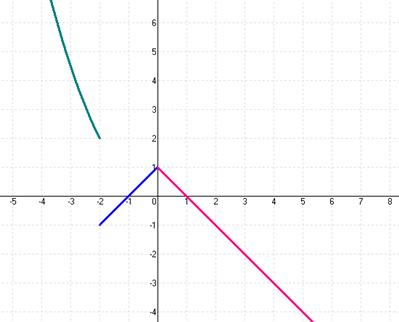
№32. 
Построим график данной функции:
Функция определена на всём множестве чисел и неэлементарная.
Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках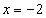 
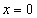
и 
.
Исследуем поведение функции в этих точках: найдём значение функции в этих точках и пределы справа и слева,
, 
. Так как 
, Следовательно функция имеет разрыв 1-го рода – скачок.
, 
. Так как 
, то в этой точке функция в этой точке непрерывна
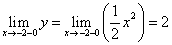
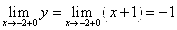
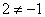
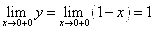
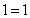
Задания 41-50. Найти производные первого порядка y’=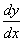 
функций:
№42. а)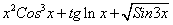
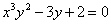
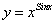
; б) 
; в) 
;
Д)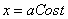 
, 
А) 
;
Б) ;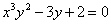
Дифференцируем обе части равенства по х: 
Разрешаем равенство относительно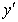 
:
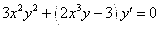
, тогда 
Окончательно:
В) ;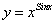
Прологарифмируем данную функцию:
Найдём производную от правой и левой части по х, считая у сложной функцией, зависящей от х.
Отсюда: 
Д) ,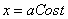
Находим 
и 
Отсюда 
Задания 51-60. Вычислить приближенно, заменяя приращение функции ее дифференциалом.
№52. 
Рассмотрим функцию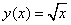 
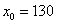
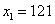
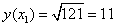
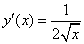
. Выберем, соответственно, 
, 
. Найдём значения функции и её производной:
, 
, 
Используя формулу для приближённых вычислений,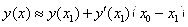 
, получим: 
№Задания 61-70. Заданную функцию исследовать методами дифференциального исчисления. На основании результатов исследований построить график функции.
№62.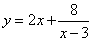 
;
Исследуем функцию, заданную формулой: 
Область определения: 
Полученное решение отметим на рисунке.
Точки пересечения с осью : нет
, 
, 
— нет решений.
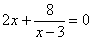
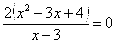
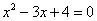
Точки пересечения с осью у: 
Пусть х=0: 
Вертикальные асимптоты: х=3
Горизонтальные асимптоты: нет.
Наклонные асимптоты: у=2х.
Предел разности исходной функции и функции 2х на бесконечности равен нулю.
Первая производная: 
=
=
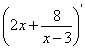
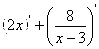
Критические точки: х=1, х=5
Случай.
Следующее уравнение равносильно предыдущему.
, 
, х-3=2, х=5
Случай . 
Следующее уравнение равносильно предыдущему.
, 
, 
, х=1
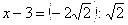
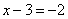
Вторая производная: 
Возможные точки перегиба: нет
Точки разрыва: х=3
Симметрия относительно оси ординат: нет 
Симметрия относительно начала координат: нет 
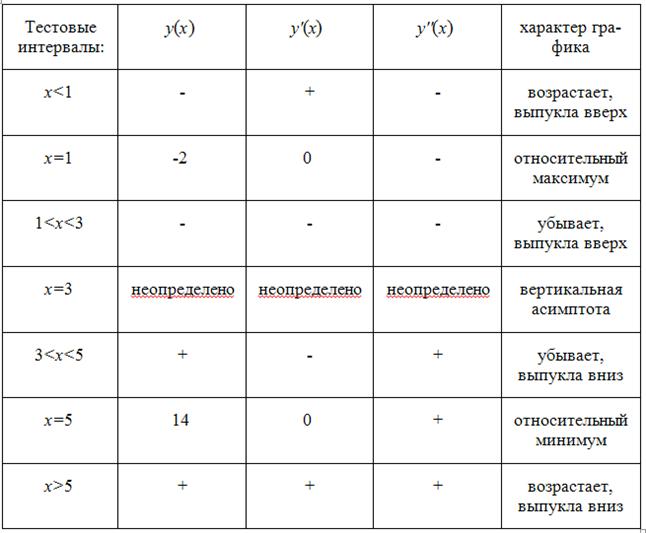
Результаты исследования функции занесем в таблицу.
Относительный минимум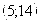 
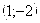
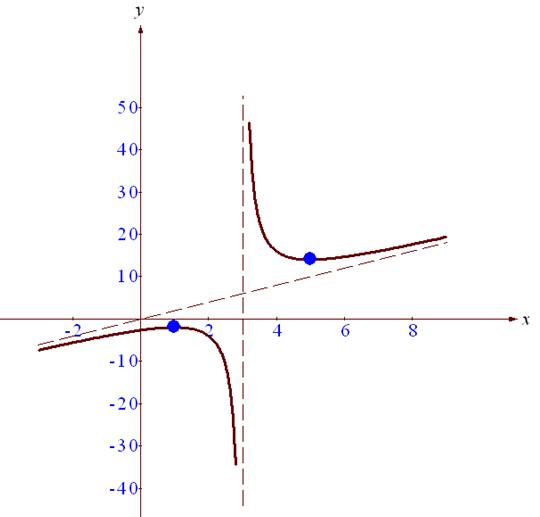
. Относительный максимум 
.
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
Множество значений функции: 
Наименьшее значение: нет
Наибольшее значение: нет
Задания 71-80. Найти интегралы.
№72. а)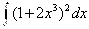 
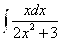
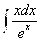
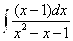
; б) 
; в) 
; г) 
;
А)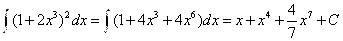 
;
Б) 
;
В)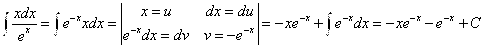 
;
Г) 
Задания 81-90. Вычислить несобственный интеграл или показать его расходимость
№82.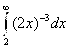 
;
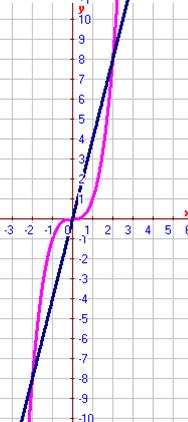
Задания 91-100. Найти площадь фигуры, ограниченной заданными линиями. Сделать рисунок.
№92.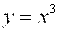 
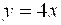
и 
;
Данные линии ограничивают две одинаковые по площади фигуры.
Тогда будем искать площадь одной части. Имеем 
По формуле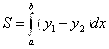 
. В нашем случае 
Тогда 
Ответ: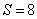 
кв. ед.
Функции нескольких переменных
Задания 101-110. Исследовать на экстремум функцию.
№102.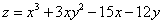 
;
Необходимое условие существования єкстремума
, 
— критические точки, подозрительные на экстремум.
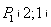
Используем достаточные условия экстремума
Найдем 
Для точки ,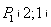 
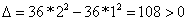
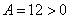
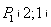
— экстремум есть, а так как 
то в т. — минимум
Для точки , 
— экстремума нет.
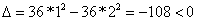
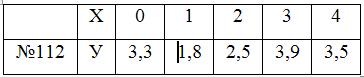
Задания 111-120. Экспериментально получены значения функции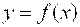 
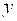
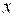
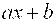
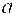
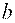
при пяти значениях аргумента, которые записаны в таблице. Предполагая, что между 
и 
имеется линейная зависимость, методом наименьших квадратов найти эмпирическую формулу 
(вычислить параметры 
и 
)
Линейное уравнение тренда имеет вид y = bt + a
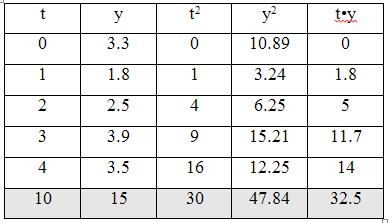
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений метода наименьших квадратов:
Для наших данных система уравнений имеет вид:
10a0 + 30a1 = 32.5
Из первого уравнения выражаем а0 и подставим во второе уравнение
🎥 Видео
Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
9 класс, 7 урок, Уравнение прямойСкачать
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
10. Параллельность и перпендикулярность плоскостей Решение задачСкачать
Уравнение параллельной прямойСкачать
Видеоурок "Канонические уравнения прямой"Скачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
Составляем уравнение прямой по точкамСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать
Уравнение плоскости через 2 точки параллельно прямойСкачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Часть 8 Уравнение прямой проходящей через точку и перпендикулярную к заданной прямойСкачать
4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать
Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать
3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать
Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать
