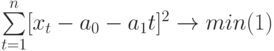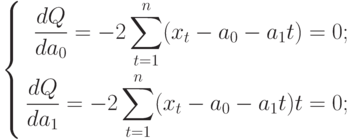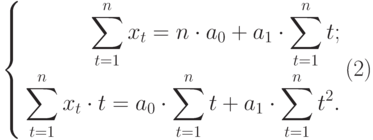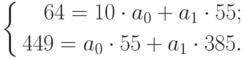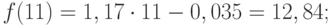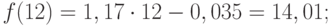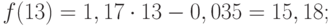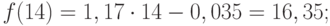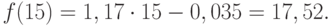- Составляющие временного ряда
- Тренд. Методы сглаживания
- Метод скользящей средней
- Метод экспоненциального сглаживания
- Методы прогнозирования
- Двойное экспоненциальное сглаживание
- Метод Хольт-Винтерса
- Мультипликативный метод Хольт-Винтерса
- Метод Хольт-Винтерса в excel
- Качество прогнозирования
- Анализ временных рядов, тренд ряда динамики, точечная оценка прогноза
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- Анализ временных рядов
- Прогноз, характеристики и параметры прогнозирования
- Уравнение тренда временного ряда
- Временные ряды
- Понятие временного ряда
- Датасеты
- Анализ временных рядов
- Импорт данных и работа в библиотеке Pandas
- Изменение шага временного ряда, сдвиг и скользящее среднее
- Построение графиков
- Разложение временного ряда на компоненты
- Стационарность
- Автокорреляция
- Моделирование и построение прогноза
- Экспоненциальное сглаживание
- Модель ARMA
- 🎥 Видео
Видео:БАС ЛР3 Динамика 9 Уравнение трендаСкачать

Составляющие временного ряда
При анализе временного ряда выделяют три составляющие: тренд, сезонность и шум. Тренд — это общая тенденция, сезонность, как следует из названия — влияния периодичности (день недели, время года и т.д.) и, наконец, шум — это случайные факторы.
Что бы понять отличие этих трёх величин, смоделируем функцию расстояния от земли до луны. Известно, что в среднем луна каждый год отдаляется на 4 см — это тренд, в течение дня луна совершает оборот вокруг земли и расстояние колеблется от
405400 км — это сезонность. Шум — это «случайные» факторы, например, влияние других планет. Если мы изобразим сумму этих трёх графиков, то мы получим временной ряд — функцию, показывающую изменение расстояния от земли до луны во времени.
Видео:Excel. Линия трендаСкачать

Тренд. Методы сглаживания
Методы сглаживания необходимы для удаления шума из временного ряда. Существуют различные способы сглаживания, основные — это метод скользящей средней и метод экспоненциального сглаживания.
Метод скользящей средней
Идея метода скользящего среднего заключается в смещении точки графика на среднее значение некоторого интервала. В качестве интервала берут нечётное количество участков, например, три — предыдущий, текущий и следующий периоды, находится среднее и принимается в качестве сглаженного значения:
У данного метода есть проблема: случайное высокое или низкое значение сильно влияют на скользящую линию. В качестве решения были введены веса. Для распределение веса используют оконные функции, основные оконные функции — это окно Дирихле (прямоугольная функция), В-сплайны, полиномы, синусоидальные и косинусоидальные:
Минусы использования скользящей средней — это сложность вычислений и некорректные данные на концах графика.
| Исходные данные | Скользящая средняя | Взвешенная скользящая средняя (синусоидальное окно, n=5) | Взвешенная скользящая средняя (окно Ганна, n=5) |
| 800 | 819 | 283 | 0 |
| 838 | 937 | 464 | 400 |
| 1172 | 1024 | 558 | 419 |
| 1286 | 1041 | 668 | 586 |
| 868 | 1037 | 682 | 643 |
| 820 | 957 | 589 | 434 |
| 854 | 909 | 509 | 410 |
| 1094 | 1190 | 552 | 427 |
| 1992 | 1340 | 777 | 547 |
| 1421 | 1349 | 943 | 996 |
| 890 | 1804 | 865 | 711 |
| 2912 | 1608 | 988 | 445 |
| 1208 | 1804 | 1099 | 1456 |
| 2204 | 1904 | 1206 | 604 |
| 1290 | 1676 | 993 | 1102 |
| 2000 | 2262 | 1066 | 645 |
| 3552 | 2510 | 1356 | 1000 |
| 3197 | 2828 | 1807 | 1776 |
| 2564 | 2937 | 1880 | 1599 |
| 2434 | 2732 | 2182 | 1282 |
| Таблица 1. Сглаживание методом скользящей средней | |||
Как видно из графика, увеличение n выдаёт более плавную функцию, таким образом нивелируя более мелкие колебания во временном ряду. Обратите внимание, что при сглаживании не имеет значения, совпадает график среднего с графиком данных или нет, целью является построение правильной формы.
Метод экспоненциального сглаживания
Метод экспоненциального сглаживания получил своё название потому, что в сглаженной функции экспоненциально убывает влияние предыдущего периода с неким коэффициентом чувствительности α. Сглаженное значение находится как разница между предыдущим действительным значением и рассчитанным значением:
Коэффициент чувствительности, α, выбирается между 0 и 1, в качестве базиса используют значение 0,3. Если есть достаточная выборка, то коэффициент подбирается путём оптимизации.
| Исходные данные | Экспоненциальное сглаживание, α=0,1 | Экспоненциальное сглаживание, α=0,6 | |
| 800 | 800 | 800 | |
| 838 | -640 | 160 | |
| 1172 | 660 | 439 | |
| 1286 | -477 | 528 | |
| 868 | 558 | 560 | |
| 820 | -415 | 297 | |
| 854 | 456 | 373 | |
| 1094 | -325 | 363 | |
| 1992 | 402 | 511 | |
| 1421 | -163 | 991 | |
| 890 | 289 | 456 | |
| 2912 | -171 | 352 | |
| 1208 | 445 | 1606 | |
| 2204 | -280 | 82 | |
| 1290 | 472 | 1290 | |
| 2000 | -296 | 258 | |
| 3552 | 466 | 1097 | |
| 3197 | -64 | 1692 | |
| 2564 | 377 | 1241 | |
| 2434 | -83 | 1042 | |
| Таблица 2. Экспоненциальное сглаживание | |||
Видео:Прогнозирование в Excel с помощью линий трендаСкачать

Методы прогнозирования
Методы прогнозирования основываются на выявлении тенденции во временном ряду и последующем использовании найденного значения для предсказания будущих значений. В методах прогнозирования выделяют тренд и сезонность, в общем случае, все типы сезонности могут быть найдены последовательными итерациями. Например, при анализе данных за год, можно выделить сезонность времени года, а в оставшемся тренде найти сезонность по дням недели и так далее.
Двойное экспоненциальное сглаживание
Двойное экспоненциальное сглаживание выдаёт сглаженное значение уровня и тенденции.
Внимание! Может возникнуть путаница, метод Хольт-Винтерса отличается терминами: тренд, сезонность и шум соответственно называются уровень, тренд и сезонность.
Smooth — сглаживание, сглаженный уровень на период τ, sτ, зависит от значения уровня на текущий период (Dτ), тренда за предыдущий период (tτ-1) и рассчитанного сглаженного значения на предыдущий период (sτ-1):
sτ = αDτ + (1 — α)(sτ-1 + tτ-1)
Trend — тенденция, тренд на период τ, tτ, зависит от рассчитанного сглаженного значения за предыдущий и текущий периоды (sτ и sτ-1) и от предыдущей тенденции:
tτ = β(sτ-sτ-1) + (1-β)tτ-1
Рассчитанные по данным формулам уровень и тренд могут быть использованы в прогнозировании:
D’τ+h = sτ + h·tτ
При расчёте, значения s и t для первого периода назначают s1 = D1 и t=0
Метод Хольт-Винтерса
Метод Хольт-Винтерса включает в себя сезонную составляющую, т.е. периодичность. Существуют две разновидности метода — мультипликативный и аддитивный. В отличие от двойного экспоненциального сглаживания, метод Хольт-Винтерса изучает также влияние периодичности.
Общая идея нахождения значений сглаженного уровня, тренда и периодичности заключается в следующем: сглаженный уровень (s — smooth, иногда используют l — level) — это базовый уровень значений, тренд (t — trend) — это показатель скорости роста, разница между сглаженными значениями текущего и предыдущего периода. Для изучения периодичности (p — period), мы разбиваем данные на периоды размером k и выделяем влияние каждого элемента (1,2. k) периода на сглаженный уровень.
Для более точных расчётов вводится показатель обратной связи.
В общем понимании, обратная связь — это влияние предыдущих значений на новые: например, когда Вы начинаете говорить, Вы регулируете громкость своего голоса в зависимости от того, что слышат Ваши уши — это и есть обратная связь.
Для начала расчётов, значения s, t и k, в самом простом виде, могут быть выбраны как sτ = Dτ, t = 0, p = 0.
Для прогнозирования используется следующая формула:
Мультипликативный метод Хольт-Винтерса
Мультипликативный метод отличается от аддитивного тем, что параметры, влияющие на периодичность и сглаженный уровень рассчитываются отношением:
Для прогнозирования используется следующая формула:
Метод Хольт-Винтерса в excel
Таблица для скачивания в форматах ods и xls.
Видео:Быстрое прогнозирование в Microsoft ExcelСкачать
Качество прогнозирования
Проверка качества прогнозирования возможна в случае наличия достаточной выборки и является важной проверкой на достоверность прогноза, для проверки и оптимизации значений α, β и γ необходимо построить прогноз на существующие данные, например, если у нас в наличии данные за пять лет и мы хотим предсказать следующий год, то необходимо построить модель на первых четырёх годах, проверить и оптимизировать коэффициенты для минимизации ошибки между прогнозом и данными на 5й год. После оптимизации модель может быть перестроена с учётом последнего периода для повышения точности, далее следует построение прогноза.
Методы оптимизации будут описаны в отдельной статье, ниже представлен пример прогнозирования методом Хольт Винтерса.
Видео:Расчет прогноза продаж легко и быстроСкачать

Анализ временных рядов, тренд ряда динамики, точечная оценка прогноза
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 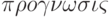
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 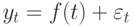

Неслучайная функция f (t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами ( t, yt ) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t ), где f (t) = a0+a1(t ).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel .
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f (t) в точках ti от значений исходного временного ряда в тех же точках ti . Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид 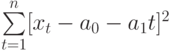
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
| t | t 2 | хt | хtt |
|---|---|---|---|
| 1 | 1 | 2 | 2 |
| 2 | 4 | 1 | 2 |
| 3 | 9 | 4 | 12 |
| 4 | 16 | 4 | 16 |
| 5 | 25 | 6 | 30 |
| 6 | 36 | 8 | 48 |
| 7 | 49 | 7 | 49 |
| 8 | 64 | 9 | 72 |
| 9 | 81 | 12 | 108 |
| 10 | 100 | 11 | 110 |
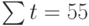 | 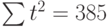 | 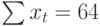 | 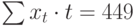 |
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f (t) имеет вид:
f (t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Временной ряд приведен в таблице. Используя средства MS Excel :
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Рассмотрим решение этой задачи средствами Microsoft Excel . При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3 рис. 14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4 рис. 14.4.
Итоговый график представлен на рисунке 14.5 рис. 14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t ), найденного по методу наименьших квадратов. Для этого в полученное для f (t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel ):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t ), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
Видео:Временные ряды и прогнозированиеСкачать

Временные ряды
Понятие временного ряда
Временной ряд (time series) — это данные, последовательно собранные в регулярные промежутки времени.
К таким данным относятся, например, цены на акции, объемы продаж чего-либо, изменения температуры с течением времени и т.д. Посмотрим на изменение обычных данных и временных рядов.
Основное отличие: перекрестные данные предполагают независимость наблюдений, во временных рядах будущее зависит от прошлого.
Работа с временными рядами предполагает два аспекта:
- Анализ временного ряда (time series analysis), т.е. понимание его структуры и закономерностей; и
- Моделирование и построение прогноза на будущее (time series forecasting)
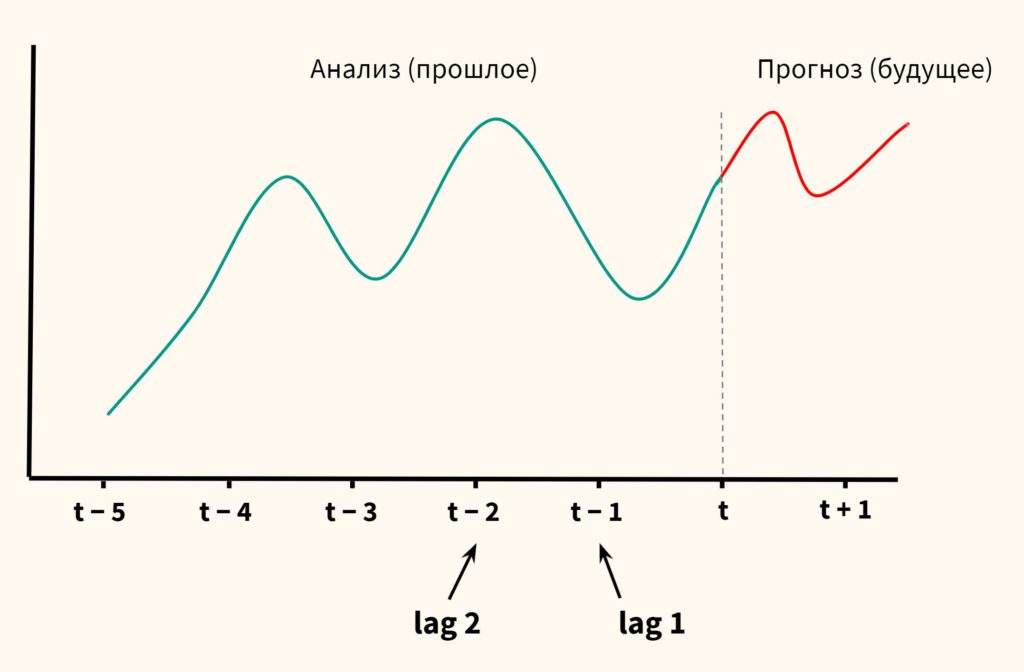
Договоримся о терминах:
- Во-первых, определим нотацию периодов. Временем t обозначим настоящее, t−1, t−2,… прошлое, t+1, t+2,… будущее.
- Во-вторых, введем важное понятие временного лага (lag), т.е. запаздывания по сравнению с заданным периодом.
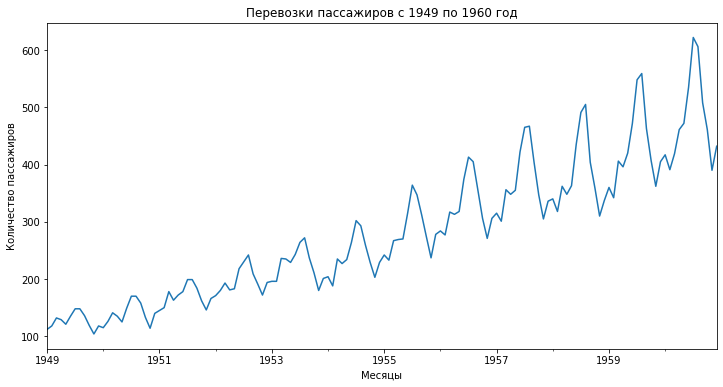
Датасеты
Мы будем использовать два популярных набора данных, а именно (1) ежемесячные данные о количестве пассажиров, перевезенных одной американской авиакомпанией с 1949 по 1960 годы и (2) ежедневные данные о родившихся в Калифорнии в 1959 году девочках.
Подгружать внешние данные в ноутбук Google Colab мы уже умеем. Можем переходить непосредственно к работе с кодом.
Анализ временных рядов
Импорт данных и работа в библиотеке Pandas
Для начала давайте импортируем данные. Пока что мы будем использовать только первый набор данных с информацией об авиаперевозках.
Сделаем дату индексом.
Питон воспринимает дату как число. Это не очень удобно, если мы хотим делать срезы и в целом изменять данные во времени. Дату можно преобразовать в специальный объект datetime.
Все эти операции также можно проделать в одну строчку.
Теперь мы можем делать срезы за определенный период, например, с августа 1949 по март 1950 года.
Обратите внимание, что в отличие от других перечней в Питоне (например, списков), во временном ряде мы получаем данные и по начальной, и по конечной дате среза (в частности, март 1950 года вошел в наш интервал).
Изменение шага временного ряда, сдвиг и скользящее среднее
Отдельно хотелось бы поговорить про возможность обобщения и изменения данных. Помимо прочего, мы можем изменить шаг (resample) нашего временного ряда, и посмотреть средние показатели перевозок, например, за год.
Кроме того, мы можем сдвинуть (shift) наши данные на n периодов вперед или назад.
Что логично, после сдвига первые два значения определяются как пропущенные (NaN или Not a number).
Мы также можем рассчитать скользящее среднее (moving average, rolling average) за n предыдущих периодов. Вначале посмотрим, что это такое.
Теперь давайте рассчитаем его для наших данных. Период, за который рассчитывается скользящее среднее, также называется окном (window).
Опять же, так как в данном случае мы использовали три месяца для расчета скользящего среднего, этот показатель недоступен для первых двух значений. В целом, скользящее среднее сглаживает временные показатели (мы это увидим на графике в следующем разделе).
Построение графиков
Для того чтобы построить график временного ряда мы можем воспользоваться инструментами, которые уже содержатся в библиотеке Pandas. Например, простым методом .plot().
График можно усложнить.
Визуализацию можно также построить с помощью библиотеки Matplotlib. Давайте выведем на одном графике перевозки пассажиров и скользящее среднее.
Как вы видите, скользящее среднее сильно сглаживает показатели. Также обратите внимание, что так как в данном случае мы взяли окно равное двенадцати месяцам, то первое значение скользящего среднего мы получили только за декабрь 1949 года (самое начало желтой кривой на графике).
В целом не стоит недооценивать важность визуальной оценки ряда на графике. Многие особенности можно выявить именно так.
Разложение временного ряда на компоненты
Выявление компонентов временного ряда (time series decomposition) предполагает его разложение на тренд, сезонность и случайные колебания. Дадим несколько неформальных определений.
- Тренд — долгосрочное изменение уровня ряда
- Сезонность предполагает циклические изменения уровня ряда с постоянным периодом
- Случайные колебания — непрогнозируемое случайное изменение ряда
В Питоне в модуле statsmodels есть функция seasonal_decompose(). Воспользуемся ей для визуализации компонентов ряда.
Перед этим импортируем второй датасет для последующего сравнения.
Теперь давайте разложим наш временной ряд по авиаперевозкам на компоненты.
Сделаем то же самое с данными о рождаемости.
Как мы видим, графики совершенно разные. В следующем разделе мы изучим это различие более подробно.
Стационарность
Стационарность (stationarity) временного ряда как раз означает, что такие компоненты как тренд и сезонность отсутствуют. Говоря более точно, среднее значение и дисперсия не меняются со смещением во времени.
Понимание того, стационарные ли у нас данные или нестационарные важно для последующего моделирования.
Стационарность процесса можно оценить визуально. Датасет о перевозках демонстрирует очевидный тренд и сезонность, в то время как в наборе данных о рождаемости этого не видно (см. графики выше).
Для более точной оценки стационарности можно применить тест Дики-Фуллера (Dickey-Fuller test). О том, что такое статистический вывод мы с вами уже говорили.
В данном случае гипотезы звучат следующим образом.
- Нулевая гипотеза предполагает, что процесс нестационарный
- Альтернативная гипотеза соответственно говорит об обратном
Применим этот тест к обоим датасетам. Используем пороговое значение, равное 0,05 (5%).
Как мы видим, вероятность (p-value) для данных о перевозках существенно выше 0,05. Мы не можем отвергнуть нулевую гипотезу. Процесс нестанионарный. Проведем тест для второго набора данных.
Результат существенно меньше 5%. Временной ряд стационарен.
Надо сказать, что наша визуальная оценка полностью совпала с математическими вычислениями.
Автокорреляция
Изучая статистику, мы с вами уже познакомились с корреляцией. Корреляция показывает силу взаимосвязи двух переменных и позволяет строить модель.
Автокорреляция также показывает степень взаимосвязи в диапазоне от –1 до 1, но только не двух переменных, а одной и той же переменной в разные моменты времени.
Допустим, у нас есть временной ряд и этот же ряд, взятый с лагом 1, 2 и 3.
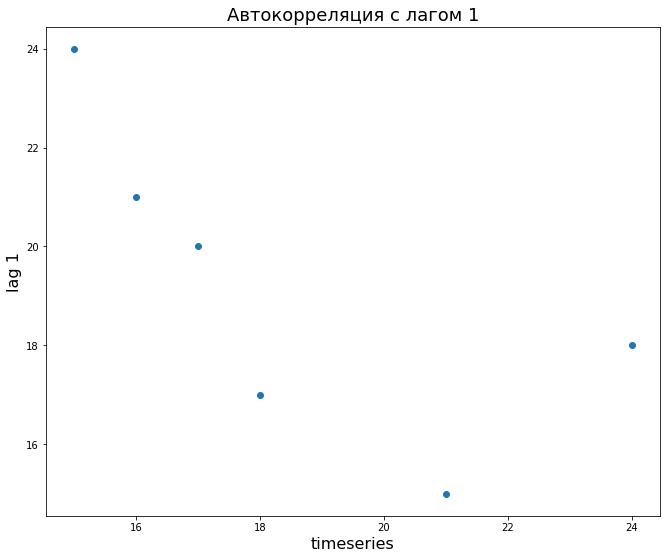
Мы можем посчитать автокорреляцию ряда с лагом 1.
Визуально это будет выглядеть следующим образом (вспомните график обычной корреляции).
Аналогично мы можем посчитать корреляцию для лагов 2 и 3 и на самом деле любого другого лага. Такие измерения автокорреляции удобно вычислить и изобразить с помощью графика автокорреляционной функции (autocorrelation function, ACF).
В частности, мы видим, что автокорреляция ряда с самим собой (первый столбец) равна 1, что логично. Второй столбец (то есть лаг 1) как раз примерно равен – 0,71.
Разные значения, полученные через np.corrcoef() и plot_acf(), объясняются небольшим различием в заложенных в этих функциях формулах.
Теперь построим график ACF для наших данных о перевозках.
Автокорреляция позволяет выявлять тренд и сезонность, а также используется при подборе параметров моделей. В частности, мы видим, что лаг 12 сильнее коррелирует с исходным рядом, чем соседние лаги 10 и 11. То же самое можно сказать и про лаг 24. Такая автокорреляция позволяет предположить наличие (ежегодных) сезонных колебаний.
То, что корреляция постоянно положительная говорит о наличии тренда. Все это согласуется с тем, что мы узнали о данных, когда раскладывали их на компоненты.
Также замечу, что синяя граница позволяет оценить статистическую значимость корреляции. Если столбец выходит за ее пределы, то автокорреляция достаточно сильна и ее можно использовать при построении модели.
Сравним полученный выше график с графиком автокорреляционной функции данных о рождаемости.
Во-первых, важно отметить, что автокорреляция в данном случае намного слабее. Во-вторых, мы не можем выявить четкой сезонности и тренда.
Моделирование и построение прогноза
На сегодняшнем занятии мы познакомимся с двумя типами моделей: экспоненциальное сглаживание и модель ARMA (и ее более продвинутые версии, ARIMA, SARIMA и SARIMAX).
Экспоненциальное сглаживание
Вновь обратимся к скользящему среднему (см. выше). В этой модели (1) всем предыдущим наблюдениям задавался одинаковый вес и (2) количество таких наблюдений было ограничено (мы называли это размером окна).
Однако логично предположить, что недавние наблюдения более важны для прогноза, чем более отдаленные. Кроме того, мы можем взять все, а не некоторые из имеющихся у нас наблюдений.
В модели экспоненциального сглаживания (exponential smoothing) или экспоненциального скользящего среднего мы как раз (1) берем все предыдущие значения и (2) задаем каждому из наблюдений определенный вес и (экспоненциально) уменьшаем этот вес по мере углубления в прошлое.
$$ hat_t = alpha cdot y_t + (1-alpha) cdot hat_ $$
где ŷt — это прогнозное значение, yt — текущее истинное значение, ŷt–1 — предыдущее прогнозное значение.
Как мы видим, прогнозное значение зависит от текущего истинного и предыдущего прогнозного значения. Важность этих значений определяется параметром альфа, который варьируется от 0 до 1. Чем альфа больше, тем больший вес у текущего наблюдения.
Формула рекурсивна, т.е. каждый раз мы умножаем (1 – α) на предыдущее прогнозное значение и так до конца временного ряда.
Практика
На Питоне эту модель не сложно прописать руками.
Для временного ряда, состоящего из 365 наблюдений (весь 1959 год), мы получим 366 значений (включая прогноз на 1 января 1960 года).
Для того чтобы представить кривую экспоненциального сглаживания на графике, добавим эти данные в исходный датафрейм births. Полностью код работы с датафреймом я приведу в ноутбуке⧉. Здесь представлю только получившийся результат.
Теперь выведем результат на графике.
Очень советую в качестве упражнения попробовать построить график с несколькими значениями альфа от 0 до 1.
Модель экспоненциального сглаживания можно усложнить и тогда она будет улавливать тренд и сезонность. Кроме того, усложненные модели способны предсказывать более одного значения (обратите внимание, здесь мы смогли сделать прогноз лишь на один день вперёд).
Теперь поговорим про модели семейства ARMA.
Модель ARMA
Модель ARMA состоит из двух компонентов.
Авторегрессия (autoregressive model, AR) — это регрессия ряда на собственные значения в прошлом. Другими словами, наши признаки в модели обычной регрессии мы заменяем значениями той же переменной, но за предыдущие периоды.
Когда мы прогнозируем значение в период t с помощью данных за предыдущий период (AR(1)), уравнение будет выглядеть следующим образом.
$$ y_t = c + varphi cdot y_ $$
где c — это константа, φ — вес модели, yt–1 — значение в период t – 1.
То, сколько предыдущих периодов использовать определяется параметром p. Обычно записывается как AR(p).
Модель скользящего среднего (moving average, MA) помогает учесть случайные колебания или отклонения (ошибки) истинного значения от прогнозного. Можно также сказать, что модель скользящего среднего — это авторегрессия на ошибку.
Обратите внимание, что скользящее среднее временного ряда, которое мы рассмотрели выше, и модель скользящего среднего — это разные понятия.
Если использовать ошибку только предыдущего наблюдения, то уравнение будет выглядеть следующим образом.
$$ y_t = mu + varphi cdot varepsilon_ $$
где μ — это среднее значение временного ряда, φ — вес модели, εt–1 — ошибка в период t – 1.
Такую модель принято называть моделью скользящего среднего с параметром q = 1 или MA(1). Разумеется, параметр q может принимать и другие значения (MA(q)).
Модель ARMA с параметрами (или как еще говорят порядками, orders) p и q или ARMA(p, q) позволяет описать любой стационарный временной ряд.
ARMA предполагает, что в данных отсутствует тренд и сезонность (данные стационарны). Если данные нестационарны, нужно использовать более сложные версии этих моделей:
- ARIMA, здесь добавляется компонент Integrated (I), который отвечает за удаление тренда (сам процесс называется дифференцированием); и
- SARIMA, эта модель учитывает сезонность (Seasonality, S)
- SARIMAX включает еще и внешние или экзогенные факторы (eXogenous factors, отсюда и буква X в названии), которые напрямую не учитываются моделью, но влияют на нее.
Параметров у модели SARIMAX больше. Их полная версия выглядит как SARIMAX(p, d, q) x (P, D, Q, s). В данном случае, помимо известных параметров p и q, у нас появляется параметр d, отвечающий за тренд, а также набор параметров (P, D, Q, s), отвечающих за сезонность.
Теперь давайте воспользуемся моделью SARIMAX для прогнозирования авиаперевозок.
Практика
В первую очередь нужно разбить данные на обучающую и тестовую выборки. Как мы помним, у нас есть данные с января 1949 года по декабрь 1960 года.
🎥 Видео
Excel для полных чайников Урок 16 Линия трендаСкачать
Временные ряды. Аддитивная и мультипликативная моделиСкачать

Аддитивная модель временного рядаСкачать

Аналитическое выравниваниеСкачать

Эконометрика. Моделирование временных рядов. Построение аддитивной модели.Скачать

Занятие 20. Временные рядыСкачать

Как построить модель временного рядаСкачать

Машинное обучение. Прогнозирование временных рядов. К.В. Воронцов, Школа анализа данных, Яндекс.Скачать

16. "Анализ и прогнозирование временных рядов", Иван ЮрченковСкачать

Лекция 14. Временные ряды и их компоненты.Скачать

Моделирование трендов и временных рядовСкачать

Уравнение тренда (устар.)Скачать

Самый простой метод определения Тренда.Скачать

02 Очистка временного ряда от аномалийСкачать