Найти уравнение прямой проходящей через точку пересечения прямых 3х 2у 7 0

Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Найдите уравнение прямой, проходящей через точку пересечения прямых.3x–2y–7 = 0 и x + 3y–6 = 0 и отсекает на оси абсцисс отрезок, равный 3.Чертеж тоже нужен.
Спасибо!

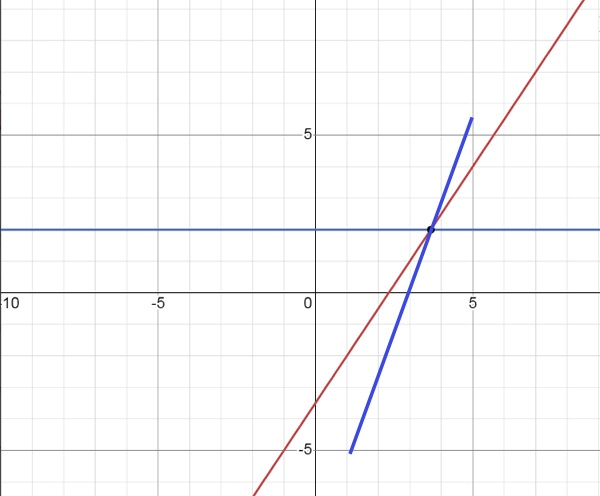
Запишем задачу в виде математического выражения.

Решим относительно y в первом уравнении

Добавляем 6 к обеим сторонам уравнения

Разделим каждый член на 3 и упростим

Разделим каждый член в выражении 3y=6 на 3

Сократить общий множитель 3

Заменим все y на 2 во всех уравнениях

Решим относительно в первом уравнении

Добавляем 11 к обеим сторонам уравнения

Разделим каждый член на 3 и упростим

Решением системы является полный набор упорядоченных пар, которые являются допустимыми решениями

Проведем прямую по двум точкам:

(x — xa)/(xb — xa) = (y — ya)/(yb — ya)

Подставим в формулу координаты точек:

(x — (11/3))/(3 — (11/3)) = (y — 2)/(0 — 2 )

В итоге получено каноническое уравнение прямой:

(x — 11/3) /(-2/3 ) = (y — 2)/(-2)

Из уравнения прямой в каноническом виде получим уравнение прямой с угловым коэффициентом:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Задача 42973 Помогите пожалуйста срочно очень.

Условие

Помогите пожалуйста срочно очень. Составить уравнение прямой проходящей через точку пересечения прямых x+2y-10=0 и 3х-7у-7=0 параллельно прямой 3х+3у-7=0

Все решения

Находим точку пересечения прямыхx+2y–10=0 и 3х–7у–7=0

Cкладываем ( т. е заменяем второе уравнение суммой:
<x+2y–10=0
<-13y+23=0 ⇒ у=23/13

Если прямые y=k_(1)x+b_(1) и y=k_(2)x+b_(2) [red]параллельны[/red], то угловые коэффициенты равны: [red]k_(1)=k_(2)[/red]

3х+3у–7=0 ⇒ 3y= — 3x+7 ⇒ y =-x+(7/3)
k=-1

Прямые, параллельные прямой 3х+3у–7=0 имеют вид:

По условию искомая прямая проходит через точку M(84/13; 23/13)

Подставляем координаты точки М в уравнение:

О т в е т. y=-x+(107/13) или 13х+13у-107=0

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Найти уравнение прямой проходящей через точку пересечения прямых 3х 2у 7 0

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Решение задачи по высшей математике №131

Найти уравнение прямой, проходящей через точку пересечения прямых l1 и l2 и отсекающей на оси абсцисс отрезок, равный d.

Уравнение прямой l1

Уравнение прямой l2

Координаты точки Р

Отсюда находим х = 6 — 3у

x = 3

Значит точка пересечения двух прямых A (3;1)
По условия отрезок равен 3, значит координата точки B (3; 0).
Найдем уравнение прямой, проходящей через точки А и В.

Здесь знаменатель равен нулю. Полагаем числитель левой части равным нулю.
Получаем

💥 Видео

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Составляем уравнение прямой по точкамСкачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнения стороны треугольника и медианыСкачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Видеоурок "Общие уравнения прямой"Скачать

Уравнение прямой, проходящей через данную точку в данном направленииСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Пересечения прямых, лучей, отрезковСкачать