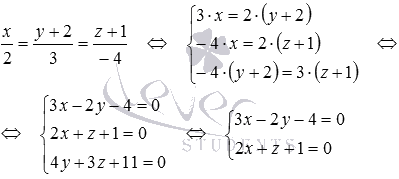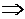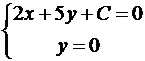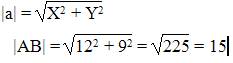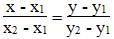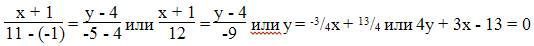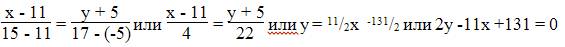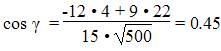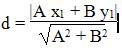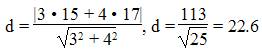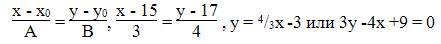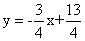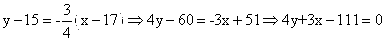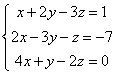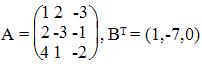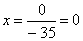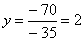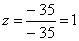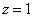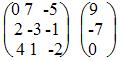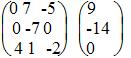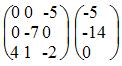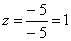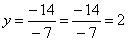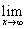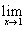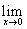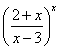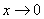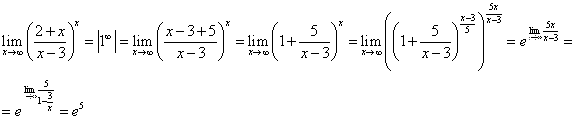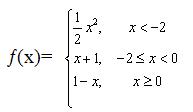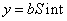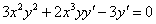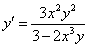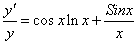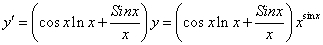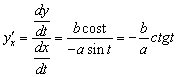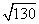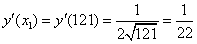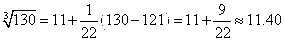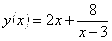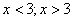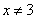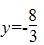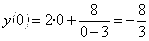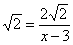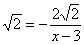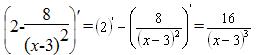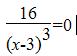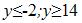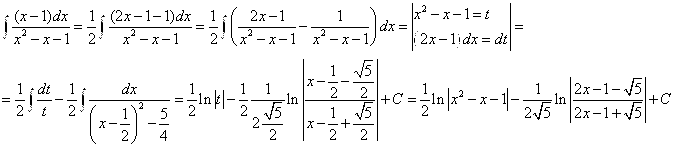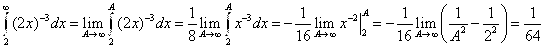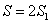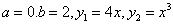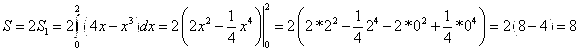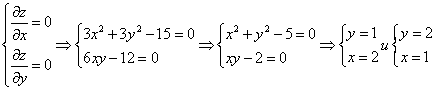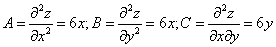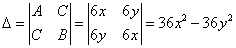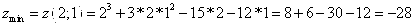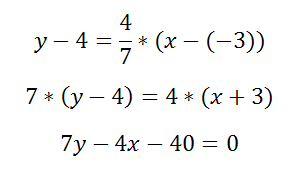Эта статья является развернутым ответом на вопрос: «Как составить уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой»? Сначала приведена необходимая теория, после чего разобраны решения характерных задач. В заключении разобрано нахождение уравнений прямой, проходящей через заданную точку трехмерного пространства параллельно заданной прямой.
Навигация по странице.
- Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
- Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
- Уравнение параллельной прямой
- Элементы линейной алгебры и аналитической геометрии, графики, матрицы, пределы, мнк
- Уравнение прямой, проходящей через точку параллельно прямой
- 🌟 Видео
Видео:Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

Уравнение прямой, проходящей через заданную точку плоскости параллельно заданной прямой.
Чтобы составление уравнения прямой, проходящей через заданную точку плоскости параллельно заданной прямой, не вызвало затруднений, вспомним важные факты.
Аксиома параллельных прямых гласит: на плоскости через точку, не лежащую на заданной прямой, проходит единственная прямая, параллельная данной. Таким образом, мы можем определить конкретную прямую a на плоскости, указав прямую линию b , которой параллельна прямая a , и точку М1 , не лежащую на прямой b , через которую проходит прямая a .
Поставим перед собой следующую задачу.
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy . Пусть в этой системе координат задана точка 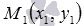
Решим поставленную задачу.
Из условия мы знаем координаты точки М1 , через которую проходит прямая a . Этих данных не достаточно, чтобы написать уравнение прямой a .
Нам еще нужно знать
Как же их найти?
По условию прямая a параллельна прямой b , тогда, на основании необходимого и достаточного условия параллельности двух прямых на плоскости, в качестве направляющего вектора прямой a мы можем принять направляющий вектор прямой b , в качестве нормального вектора прямой a мы можем взять нормальный вектор прямой b , а угловой коэффициент прямой a равен угловому коэффициенту прямой b (или они оба бесконечны).
Таким образом, чтобы в прямоугольной системе координат на плоскости написать уравнение прямой a , проходящей через заданную точку 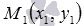
- или координаты направляющего вектора прямой b (
),
- или координаты нормального вектора прямой b (
),
- или угловой коэффициент прямой b (
),
принять их соответственно в качестве
- координат направляющего вектора прямой a (
),
- координат нормального вектора прямой a (
),
- углового коэффициента прямой a (
),
и записать требуемое уравнение прямой a соответственно в виде
или
,
,
.
Внесем ясности – приведем примеры с подробными решениями на каждый случай.
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 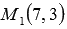
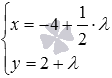
Из параметрических уравнений прямой 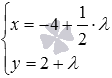
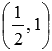
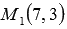
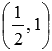
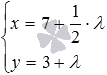
Это и есть искомые уравнения прямой, проходящей через заданную точку 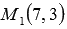
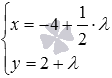
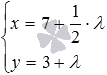
Иногда требуется составить уравнение прямой определенного вида, проходящей через заданную точку плоскости параллельно заданной прямой. В этом случае сначала записываем уравнение прямой, которое проще всего получить, после чего приводим его к нужному виду.
Составьте уравнение прямой в отрезках, если эта прямая в прямоугольной системе координат Oxy проходит через точку плоскости с координатами 
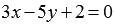
Очевидно, нормальным вектором прямой, общее уравнение которой имеет вид 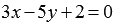
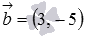

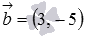
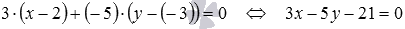

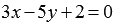
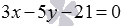
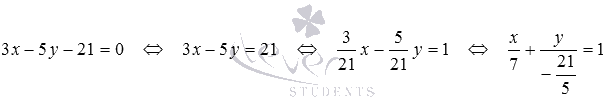
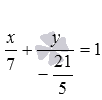
Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 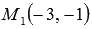
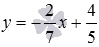
Мы знаем, что угловые коэффициенты параллельных прямых равны (или бесконечны), тогда 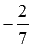
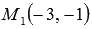
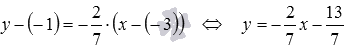
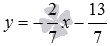
Итак, уравнение прямой a , проходящей через заданную точку плоскости M1 параллельно заданной прямой b , проще всего записывать в таком виде, в котором записано уравнение заданной прямой b .
Видео:Уравнение параллельной прямойСкачать

Уравнения прямой, проходящей через заданную точку пространства параллельно заданной прямой.
В трехмерном пространстве через точку М1 , не лежащую на прямой b , проходит единственная прямая a , параллельная прямой b . Таким образом, прямую в пространстве можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая b некоторыми уравнениями прямой в пространстве и точка 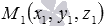
Направляющим вектором прямой a является направляющий вектор прямой b . Таким образом, по известным уравнениям прямой b мы можем определить координаты ее направляющего вектора, а, следовательно, и координаты направляющего вектора прямой a . После этого мы можем записать канонические уравнения прямой a в пространстве и параметрические уравнения прямой a в пространстве, так как известны координаты точки, лежащей на прямой a , и координаты направляющего вектора прямой a .
Рассмотрим решения примеров.
Напишите уравнения прямой, которая проходит через начало прямоугольной системы координат Oxyz в трехмерном пространстве параллельно прямой 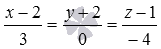
Очевидно, направляющим вектором прямой 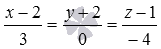
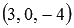
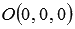
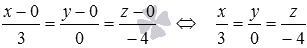
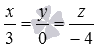
От канонических уравнений прямой a при необходимости можно будет перейти к уравнениям двух плоскостей, пересекающихся по прямой a .
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы три точки 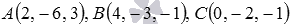
Направляющим вектором прямой, проходящей через точку С параллельно прямой АВ , является вектор 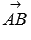
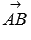
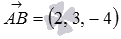
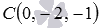
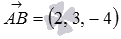
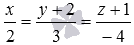
Осталось получить уравнения двух пересекающихся плоскостей, задающих эту прямую:
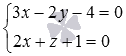
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение параллельной прямой
Альтернативная формула:
Прямая, проходящая через точку M1(x1; y1) и параллельная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).
Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника 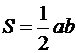
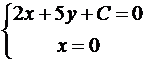
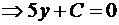
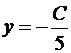
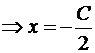
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 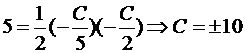
Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /7x – 4 /7 (здесь a = 5 /7). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .
Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.
Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).
Видео:Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Элементы линейной алгебры и аналитической геометрии, графики, матрицы, пределы, мнк
Элементы линейной алгебры и аналитической геометрии
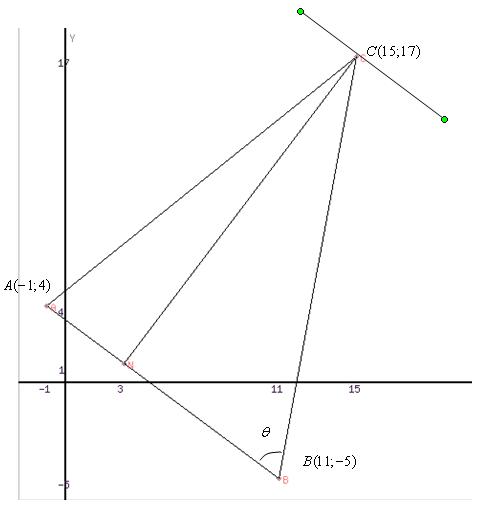
Задания 1-10. Даны координаты точек: А(х1;у1), В(х2;у2), С(х3;у3).
Значения координат точек приведены в таблице к этому заданию.
А) длину отрезка АВ;
Б) уравнение прямых АВ и ВС, проведенных через точки А, В и В, С соответственно;
В) угол θ между прямыми АВ и ВС;
Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;
Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;
Е) построить чертеж, на котором показать заданные точки, угол θ и прямые.
Координаты векторов находим по формуле: X = xj — xi; Y = yj — yi
Здесь X, Y координаты вектора; xi, yi — координаты точки Аi; xj, yj — координаты точки Аj
Для вектора AB X = x2 — x1; Y = y2 — y1
X = 11—1 = 12; Y = -5-4 = -9
А) длина отрезка АВ
Длина вектора a(X;Y) выражается через его координаты формулой:
Б) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
Уравнение прямой AB
Каноническое уравнение прямой:
Уравнение прямой BC
Каноническое уравнение прямой:
В) угол θ между прямыми АВ и ВС;
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле: 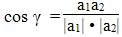
Найдем угол между сторонами BA и BC
γ = arccos(0.45) = 63.440
Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;
Длина высоты треугольника, проведенной из вершины C
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:
Найдем расстояние между точкой C(15;17) и прямой AB (4y + 3x — 13 = 0)
Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой
Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Найдем точку пересечения с прямой AB:
Имеем систему из двух уравнений:
Из первого уравнения выражаем y и подставим во второе уравнение.
Получаем: x = 3, y = 1
Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;
Уравнение прямой, проходящей через данную точку С(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y — y1 = k(x — x1).
Это уравнение определяет пучок прямых, проходящих через точку С(x1, y1), которая называется центром пучка. А k — это коэффициент при х уравнения прямой АВ
Тогда получим
Е) построим чертеж
Задания 11-20. Решить систему уравнений двумя способами (по формулам Крамера и методом Гаусса)
№12.
По формулам Крамера.
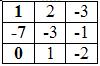
Запишем систему в виде:
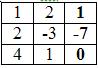
∆ = 1 • (-3 • (-2)-1 • (-1))-2 • (2 • (-2)-1 • (-3))+4 • (2 • (-1)-(-3 • (-3))) = -35 = -35
Заменим 1-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆1 = 1 • (-3 • (-2)-1 • (-1))-(-7 • (2 • (-2)-1 • (-3)))+0 • (2 • (-1)-(-3 • (-3))) = 0
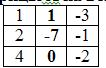
Заменим 2-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆2 = 1 • (-7 • (-2)-0 • (-1))-2 • (1 • (-2)-0 • (-3))+4 • (1 • (-1)-(-7 • (-3))) = -70
Заменим 3-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆3 = 1 • (-3 • 0-1 • (-7))-2 • (2 • 0-1 • 1)+4 • (2 • (-7)-(-3 • 1)) = -35
Выпишем отдельно найденные переменные: 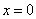
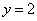
Запишем систему в виде расширенной матрицы:
Умножим 1-ую строку на (2). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Добавим 2-ую строку к 1-ой:
Теперь исходную систему можно записать как:
Из 1-ой строки выражаем z:
Из 2-ой строки выражаем у:
Из 3-ой строки выражаем x:
Введение в математический анализ.
Производная и ее приложения.
Задания 21-30. Найти указанные пределы, не пользуясь правилом Лопиталя:
№22. а) 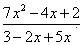
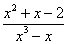
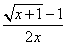
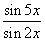
А) 
Б) 
В) 
Г) 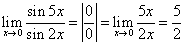
Использовали 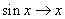
Д)
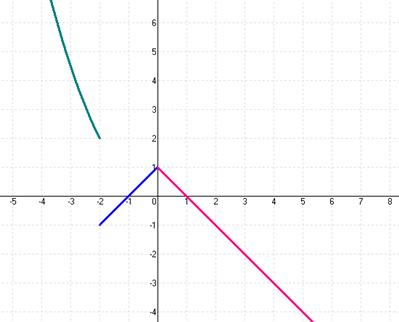
Задания 31-40. Задана функция y=ƒ(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
№32.
Построим график данной функции:
Функция определена на всём множестве чисел и неэлементарная.
Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках 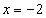
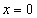
Исследуем поведение функции в этих точках: найдём значение функции в этих точках и пределы справа и слева,
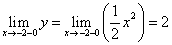
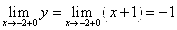
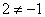

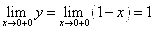
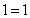
Задания 41-50. Найти производные первого порядка y’= 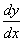
№42. а)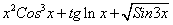
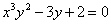
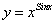
Д) 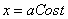
А) 
Б) 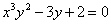
Дифференцируем обе части равенства по х:
Разрешаем равенство относительно 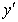
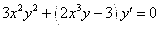
Окончательно:
В) 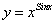
Прологарифмируем данную функцию:
Найдём производную от правой и левой части по х, считая у сложной функцией, зависящей от х.
Отсюда:
Д) 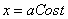
Находим 
Отсюда
Задания 51-60. Вычислить приближенно, заменяя приращение функции ее дифференциалом.
№52.
Рассмотрим функцию 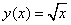
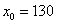
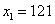
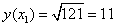
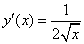
Используя формулу для приближённых вычислений, 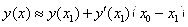
№Задания 61-70. Заданную функцию исследовать методами дифференциального исчисления. На основании результатов исследований построить график функции.
№62. 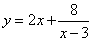
Исследуем функцию, заданную формулой:
Область определения:
Полученное решение отметим на рисунке.
Точки пересечения с осью : нет
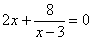
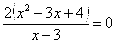
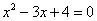
Точки пересечения с осью у:
Пусть х=0:
Вертикальные асимптоты: х=3
Горизонтальные асимптоты: нет.
Наклонные асимптоты: у=2х.
Предел разности исходной функции и функции 2х на бесконечности равен нулю.
Первая производная:
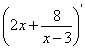
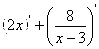
Критические точки: х=1, х=5
Случай.
Следующее уравнение равносильно предыдущему.


Случай .
Следующее уравнение равносильно предыдущему.

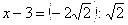
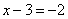
Вторая производная:
Возможные точки перегиба: нет
Точки разрыва: х=3
Симметрия относительно оси ординат: нет
Симметрия относительно начала координат: нет
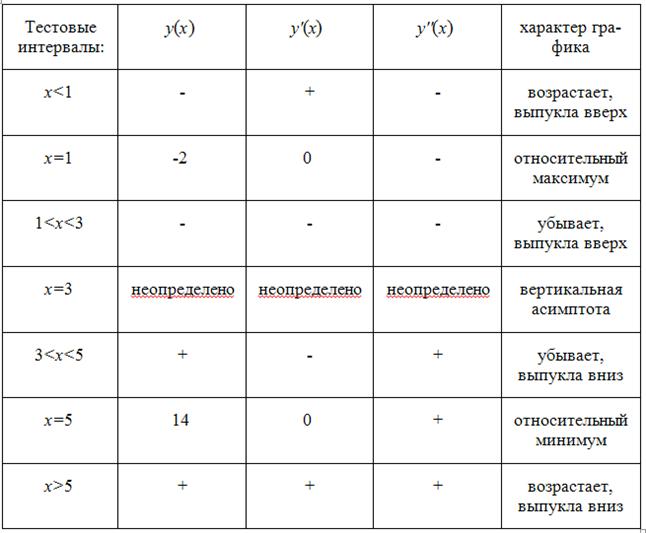
Результаты исследования функции занесем в таблицу.
Относительный минимум 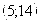
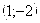
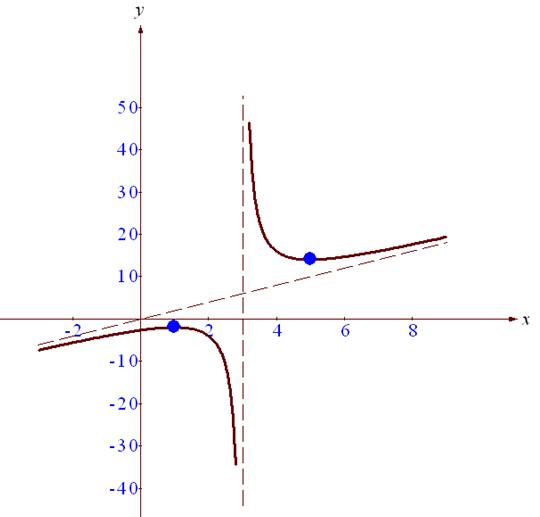
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
Множество значений функции:
Наименьшее значение: нет
Наибольшее значение: нет
Задания 71-80. Найти интегралы.
№72. а) 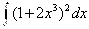
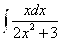
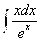
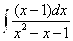
А) 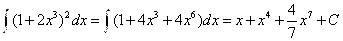
Б) 
В) 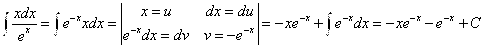
Г)
Задания 81-90. Вычислить несобственный интеграл или показать его расходимость
№82. 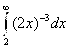
Задания 91-100. Найти площадь фигуры, ограниченной заданными линиями. Сделать рисунок.
№92. 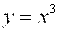
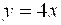
Данные линии ограничивают две одинаковые по площади фигуры.
Тогда будем искать площадь одной части. Имеем
По формуле 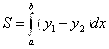
Тогда
Ответ: 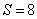
Функции нескольких переменных
Задания 101-110. Исследовать на экстремум функцию.
№102. 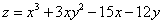
Необходимое условие существования єкстремума
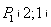

Используем достаточные условия экстремума
Найдем
Для точки 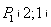
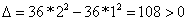
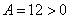
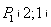
Для точки 
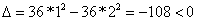
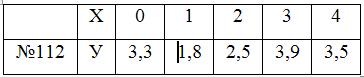
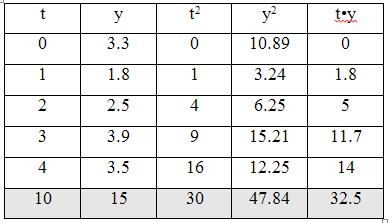
Задания 111-120. Экспериментально получены значения функции 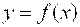
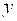
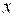
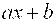
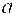
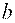
Линейное уравнение тренда имеет вид y = bt + a
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений метода наименьших квадратов:
Для наших данных система уравнений имеет вид:
10a0 + 30a1 = 32.5
Из первого уравнения выражаем а0 и подставим во второе уравнение
Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Уравнение прямой, проходящей через точку параллельно прямой
Пусть прямая, проходящая через точку K1(x1;y1) и параллельная прямой y=kx+b, записывается в виде уравнения:
Это уравнение называется уравнением прямой, проходящей через данную точку K1(x1;y1) параллельно данной прямой y=kx+b
Пример 1
Составить уравнение прямой, проходящей через точку M(-3;4) и параллельно прямой
4x-7y+1=0
Решение
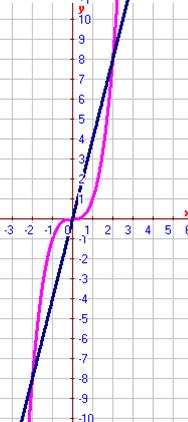
Данную прямую можно представить уравнением y=4/7x+1/7 (здесь k=4/7). Уравнение искомой прямой есть
Решение представим на графике
Пример 2
Составить уравнение прямой, проходящей через точку (-3;4) и параллельно прямой
5x+6=0
Решение
Здесь A=5, B=0, получаем 5(x+3)=0, т.е. x+2=0. В этом случае формула неприменима.
🌟 Видео
Часть 8 Уравнение прямой проходящей через точку и перпендикулярную к заданной прямойСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Составляем уравнение прямой по точкамСкачать

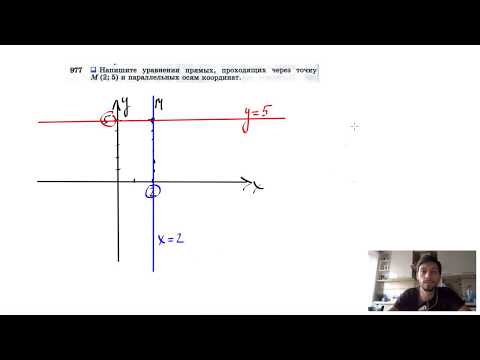
№977. Напишите уравнения прямых, проходящих через точку М (2; 5) и параллельных осям координат.Скачать
Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать

Уравнение плоскости через 2 точки параллельно прямойСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение прямой, проходящей через начало координатСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Видеоурок "Канонические уравнения прямой"Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

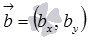 ),
),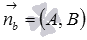 ),
),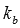 ),
),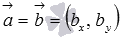 ),
),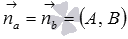 ),
),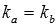 ),
),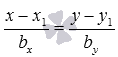 или
или 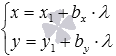 ,
,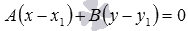 ,
,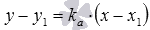 .
.