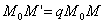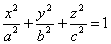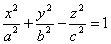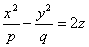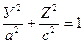Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

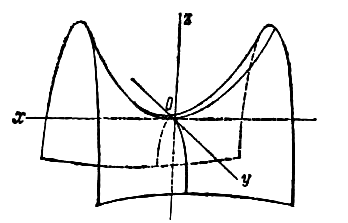
Глава 46. Поверхности второго порядка
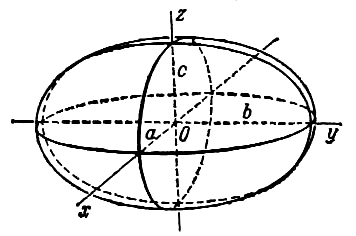
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
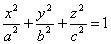
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.
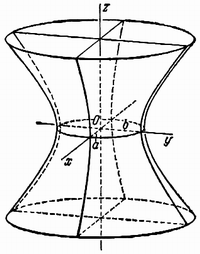
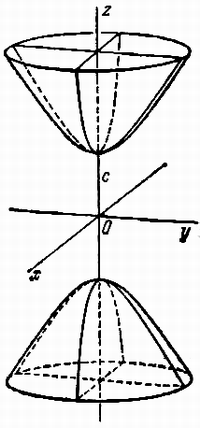
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
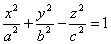
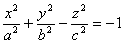
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
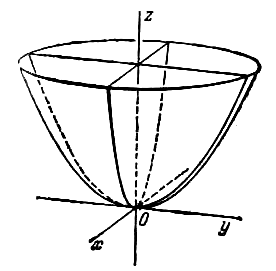
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
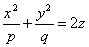
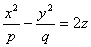
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой 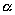
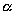
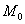
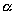
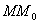
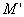
и чтобы после перемещения точка осталась с той же стороны от плоскости 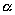
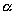
Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия 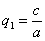
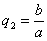
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом 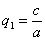
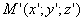
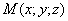
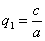
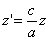
Таким образом, мы получаем искомые выражения:
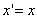
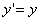
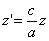
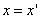
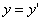
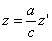
Предположим, что M(x; y; z ) — произвольная точка сферы
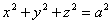
Заменим здесь x, y, z их выражениями (7); получим
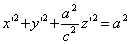
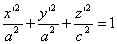
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
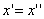
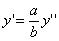
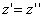
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
имеет две системы прямолинейных образующих, которые определяются уравнениями:
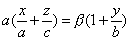
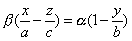
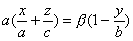
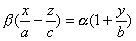
где 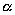
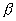
также имеет две системы прямолинейных образующих, которые определяются уравнениями
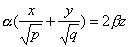
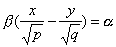
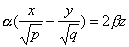
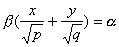
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Будь умным!
Работа добавлена на сайт samzan.net: 2015-07-05
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.
Аналитическая геометрия Практическое занятие 13-14 (06-13, 07-14.12.2013)Группы: ИМ13-05,06
«>Поверхности второго порядка
«>Задачи: №№ 10.5, 10.11, 10.30, 10.37, 10.62, 10.43, 10.82 [5].
;text-decoration:underline»>Задание 10.5. «> Написать уравнение сферы:
«>1) с центром в точке «> и радиусом «>; «>
«>2) с центром в точке «> и радиусом 1 «>.
;text-decoration:underline»>Задание 10.11. «> Найти ось вращения поверхности, изобразить поверхность:
;text-decoration:underline»>Задание 10.30. «> Найти уравнение поверхности, получаемой вращением параболы «>: 1) вокруг оси » xml:lang=»en-US» lang=»en-US»>Oz «>; 2) вокруг оси » xml:lang=»en-US» lang=»en-US»>Ox «>.
;text-decoration:underline»>Задание 10.37. «> Найти уравнение прямого кругового цилиндра радиуса «> с осью «>.
;text-decoration:underline»>Задание 10.62. «> Найти уравнение конуса с вершиной в точке «> и направляющей окружностью «>, «>.
;text-decoration:underline»>Задание 10.43. «> Найти уравнение конуса с вершиной в точке «>, касающегося сферы «>.
;text-decoration:underline»>Задание 10.82. «> Найти уравнение плоскости, проходящей через точки «> и «> и пересекающей параболоид «> по паре прямых.
«>5. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре, 2-изд. М.: Наука, 2004.
«>Поверхности второго порядка
«>Задачи: №№ 10.6, 10.12(1), 10.3, 10.38, 10.58, 10.63, 10.83 [5].
;text-decoration:underline»>Задание 10.6. «> Найти координаты центра » xml:lang=»en-US» lang=»en-US»>C «> и радиус » xml:lang=»en-US» lang=»en-US»>R «> сферы:
;text-decoration:underline»>Задание 10.12 (1). «> Определить тип поверхности, найти ось вращения, координаты вершин, изобразить поверхность: 1) «>.
;text-decoration:underline»>Задание 10.3. «> Семейство поверхностей задано в прямоугольной системе координат уравнением, содержащим произвольный параметр «>. Определить тип поверхности при всевозможных «>:
;text-decoration:underline»>Задание 10.38. «> Найти уравнение прямого кругового цилиндра, проходящего через точку «> и имеющего ось «>.
;text-decoration:underline»>Задание 10.58. «> Найти уравнение цилиндра с образующей, параллельной оси » xml:lang=»en-US» lang=»en-US»>Oz «>, и направляющей окружностью «>, «>.
;text-decoration:underline»>Задание 10.63. «> Найти уравнение эллипсоида, плоскости симметрии которого совпадают с плоскостями координат, содержащего точку «> и окружность «>, «>.
;text-decoration:underline»>Задание 10.83. «> Найти уравнение плоскости, пересекающей гиперболоид «> по паре прямых, проходящих через точку «>.
«>5. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре, 2-изд. М.: Наука, 2004.

алыпты физиология кафедрасы ТЕСТ Орталы
Материалы собраны группой SamZan и находятся в свободном доступе
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Цилиндрические поверхности
Поверхность, составленная из всех прямых, пересекающих данную линию L и параллельных данной прямой l, называется цилиндрической поверхностью. При этом линия L называется направляющей цилиндрической поверхности, а каждая из прямых, составляющих эту поверхность и параллельных прямой 
Построим цилиндрическую поверхность с образующими, параллельными оси Oz, и направляющей L . Покажем, что уравнение этой поверхности есть уравнение (4), если его отнести к системе координат в пространстве Oxyz. Пусть М (х; у; z) -любая фиксированная точка построенной цилиндрической поверхности. Обозначим через N точку пересечения направляющей L и образующей, проходящей через точку М. Точка N, очевидно, есть проекция точки М на плоскость Оху. Поэтому точки М и N имеют одну и ту же абсциссу х и одну и ту же ординату у. Но точка N лежит на кривой L, и ее координаты х и у удовлетворяют уравнению (4) этой кривой. Следовательно, этому уравнению удовлетворяют и координаты точки М (х; у; z), так как оно не содержит z. Таким образом, координаты любой точки М (х; у;z) данной цилиндрической поверхности удовлетворяют уравнению (4). Координаты же точек, не лежащих на этой поверхности, уравнению (4) не удовлетворяют, так как эти точки проектируются на плоскость Оху вне кривой L. Таким образом, не содержащее z уравнение F(x, y) = 0, если его отнести к системе координат в пространстве Oxyz, является уравнением цилиндрической поверхности с образующими, параллельными оси Oz, и направляющей L, которая в плоскости Оху задается тем же уравнением F (х, у) = 0.
В пространстве Оху направляющая L определяется системой двух уравнений:

Алогично можно показать, что уравнение F (x, z) = 0, не содержащее у, и уравнение F (у, z) = 0, не содержащее х, определяют в пространстве Oxyz цилиндрические поверхности с образующими, параллельными соответственно осям Оу и Ох.
Рассмотрим примеры цилиндрических поверхностей.
1. Поверхность, определяемая уравнением

является цилиндрической и называется эллиптическим цилиндром (рис. 2). Ее образующие параллельны оси Oz, а направляющей является эллипс с полуосями а и Ь, лежащий в плоскости Оху. В частности, если a = b, то направляющей является окружность, а поверхность является прямым круговым цилиндром. Его уравнение
2.Цилиндрическая поверхность, определяемая уравнением

называется гиперболическим цилиндром (рис. 3). Образующие этой поверхности параллельны оси Оу, а направляющей служит расположенная в плоскости Охz гипербола с действительной полуосью a и мнимой полуосью b.

3. Цилиндрическая поверхность, определяемая уравнением

Называется параболическим цилиндром (рис.4). Ее направляющей является парабола, лежащая в плоскости Oyz, а образующие параллельны оси Ох.
Замечание. Как известно, прямая в пространстве может быть задана уравнениями различных пар плоскостей, пересекающихся по этой прямой. Подобно этому кривая в пространстве может быть задана с помощью уравнений различных поверхностей, пересекающихся по этой кривой. Например, окружность С, получающаяся в сечении плоскостью z = 3 сферы 

С другой стороны, эта окружность может быть получена как линия пересечения плоскости z = 3 и прямого кругового цилиндра 
В дальнейшем, исследуя форму той или иной поверхности с помощью сечений, параллельных координатным плоскостям, мы не разбудем пользоваться цилиндрическими поверхностями, проектирующими эти сечения на координатные плоскости. Это позволит так же, как в рассмотренном примере, судить о размерах и форме указанных сечений, а тем самым и о форме исследуемых поверхностей.
Конические поверхности.
Поверхность, составленная из всех прямых, пересекающих данную линию L и проходящих через данную точку Р, называется конической поверхностью. При этом линия L называется направляющей конической поверхности, точка Р — ее вершиной, а каждая из прямых, составляющих коническую поверхность, образующей.
В качестве примера рассмотрим коническую поверхность с вершиной в начале координат, для которой направляющей является эллипс:

с полуосями а и b, лежащий в плоскости Z = c. Эта поверхность называется конусом второго порядка. Выведем ее уравнение.
Рассмотрим произвольно выбранную точку М (х; у; z ) конической поверхности и проведем через нее образующую ОМ, пересекающуюся с направляющей в точке N (X; Y; с) (рис. 5). Составим уравнение прямой ОМ, проходящей через точки 0 (0; 0; 0) и N (X; У; с)
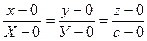

Отсюда X = cx/z; Y = cy/z. Подставив эти выражения во второе из уравнений эллипса (11), получим 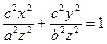

Мы получили уравнение конуса второго порядка. В частности, если а = b, то направляющей является окружность
а поверхность является прямым круговым конусом. Его уравнение
 |

Поверхность вращения.
Пусть линия L, лежащая в плоскости Oyz, задана уравнениями

Рассмотрим поверхность, образованную вращением этой линии относительно оси Оz (рис. 6). ( Текущие координаты линии L мы обозначаем большими буквами X, Y в Z, чтобы отличить их от текущих координат х, у, z поверхности вращения.)
Эта поверхность называется поверхностью вращения. Найдем ее уравнение. Пусть М (х; у; z) — произвольно выбранная точка поверхности вращения. Проведем через точку М плоскость, перпендикулярную оси Oz, и обозначим точки пересечения этой плоскости с осью Oz и кривой L соответственно через К и N. Отрезки КМ и KN являются радиусами одной и той же окружности. Поэтому КМ = KN. Но длина отрезка KN равна абсолютной величине ординаты Y точки N, т. е. KN = |Y|, a KM = OP = 
| Y |= 
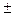

Так как точка N лежит на линии L, заданной уравнениями (12), то координаты Y и Z точки N удовлетворяют второму из этих уравнений. Подставляя в него вместо Y и Z, соответственно, равные им величины 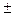


которому удовлетворяют координаты любой точки М (х; у; z) поверхности вращения. Можно показать, что координаты точек, не лежащих на этой поверхности, уравнению (13) не удовлетворяют. Таким образом, уравнение (13) является уравнением поверхности вращения относительно оси Оz линии L, определяемой уравнениями (12). Уравнение (13) получается из второго уравнения системы (12) заменой в нем координат Y и Z координатами х, у и z по формулам:

Замечание. Мы считали, что кривая L задана в плоскости Oyz и вращается относительно оси Oz. Однако кривая L может быть задана и в другой координатной плоскости и может вращаться относительно другой координатной оси. Формулы, подобные формулам (12), (13) и (14), легко составить.
Пример. Найти уравнение поверхности вращения эллипса
относительно оси Оz.
Решение. Записав уравнение эллипса в виде
и заменяя в нем по формулам (14) Y и Z текущими координатами х, у и z поверхности вращения, получим искомое уравнение 
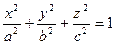
Полученная поверхность называется эллипсоидом вращения.



Поверхность, определяемая уравнением
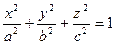
Называется эллипсоидом. Числа а, b и с называются полуосями эллипсоида. Так как в уравнение (15) текущие координаты входят в четных степенях, то эллипсоид симметричен относительно координатных плоскостей. Чтобы установить форму эллипсоида, будем пересекать его плоскостями, параллельными координатным плоскостям. Покажем, что если пересечь эллипсоид плоскостью z = h (| h | с эллипсоид с плоскостью z = h, очевидно, не пересекается. Аналогично можно показать, что при пересечении эллипсоида плоскостями х = h (| h | 2 + z 2 = а 2 .
Гиперболоиды.
Поверхность, определяемая уравнением

называется однополостным гиперболоидом. Эта поверхность имеет три плоскости симметрии — координатные плоскости, так как текущие координаты х, у и z входят в уравнение (18) в четных степенях. Пересекая однополостный гиперболоид плоскостью у = 0, получим лежащую в плоскости Oxz гиперболу ABCD (рис. 8)
Аналогично, в сечении однополостного гиперболоида плоскостью х = 0 получится гипербола EFGH
лежащая в плоскости Oyz.
При пересечении однополостного гиперболоида плоскостью z = h получится эллипс BFCG, уравнения которого имеют вид: 
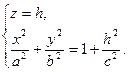
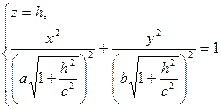
Полуоси этого эллипса 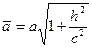

При а = b получим однополостный гиперболоид
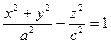
При пересечении его плоскостями z = h получаются окружности
В п. 2 и 3 рассматривались цилиндрические и конические поверхности каждая из которых составлена из прямых. Оказывается, однополостный гиперболоид можно также рассматривать как поверхность, составленную из прямых линий. Рассмотрим прямую, определяемую уравнениями:

в которых а, b и с — полуоси однополостного гиперболоида, а 
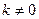
Перемножив левые и правые части этих уравнений, получим :
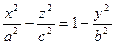

т. е. получим уравнение однополостного гиперболоида.
Таким образом, уравнение однополостного гиперболоида является следствием системы уравнений (20). Поэтому координаты любой точки М (х; у; z), удовлетворяющие системе (20), удовлетворяют также и уравнению (18) однополостного гиперболоида. Иными словами, все точки прямой (20) принадлежат гиперболоиду (18). Меняя значения k, мы получим целое семейство прямых, лежащих на поверхности (18). Аналогично можно показать, что однополостному гиперболоиду принадлежат все прямые семейства:

Где l — произвольный параметр.
Можно также показать, что через каждую точку однополостного гиперболоида проходит по одной прямой каждого из указанных семейств. Таким образом, однополостный гиперболоид можно рассматривать как поверхность, составленную из прямых линий (рис. 9). Эти прямые называются прямолинейными образующими однополостного гиперболоида.
Возможность составления поверхности однополостного гиперболоида из прямых линий используется в строительной технике. Так, например, по конструкции, предложенной инженером Шуховым , в Москве была сооружена радиомачта с помощью балок, расположенных по прямолинейным образующим однополостного гиперболоида.
Поверхность, определяемая уравнением

называется двуполостным гиперболоидом.
Координатные плоскости являются плоскостями симметрии для двуполостного гиперболоида. Пересекая эту поверхность координатными плоскостями Oxz и Оуz, получим соответственно гиперболы
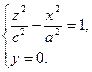



Если двуполостный гиперболоид пересечь плоскостью
z = h (при | h |>c ), то в сечении получится эллипс


возрастающими при возрастании | h |. При | h | c) получится окружность


Параболоиды.
Эллиптическим параболоидом называется поверхность, определяемая уравнением

при условии, что р и q имеют одинаковые знаки. В дальнейшем, для определенности, будем считать, что р>0, q>0.
При пересечении эллиптического параболоида координатными плоскостями Oxz и Oyz получатся, соответственно, параболы

а при пересечении плоскостью z = h (h >0) — эллипс
с полуосями 

p = q получим параболоид вращения

Поскольку х и у входят в уравнение (24) в четных степенях, эллиптический параболоид имеет две плоскости симметрии: Oxz и Oyz.
Рис.11
Рис.12.
Гиперболическим параболоидом называется поверхность, определяемая уравнением

при условии, что р и q имеют одинаковые знаки. (В дальнейшем, для определенности, будем считать, что р>0, q>0.)
Пересекая эту поверхность плоскостью Oxz, получим параболу
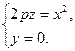
При пересечении гиперболического параболоида плоскостью x = h получится парабола

При различных значениях h получится целое семейство парабол, лежащих в плоскостях, параллельных плоскости Oyz и имеющих одинаковый параметр q.
Гиперболический параболоид можно рассматривать как поверхность, описываемую движением любой из этих парабол при условии, что плоскость движущейся параболы остается параллельной плоскости Oyz, ось симметрии параболы остается в плоскости Oxz, а вершина движется по параболе (27). Пересекая гиперболический параболоид плоскостью z = h, получим (при 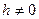

|
На рис. 12 показано расположение этой гиперболы для двух случаев: h >0 и h
🎬 Видео
Уравнение плоскости через 3 точкиСкачать

Составляем уравнение прямой по точкамСкачать

Уравнение окружности (1)Скачать

9 класс, 7 урок, Уравнение прямойСкачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Решение биквадратных уравнений. 8 класс.Скачать

Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Уравнение прямой, проходящей через две точкиСкачать