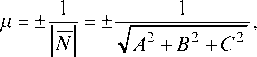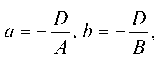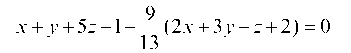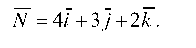В этой статье собрана информация, необходимая для решения задачи составления уравнения плоскости, проходящей через заданную прямую и заданную точку. После решения этой задачи в общем виде мы приведем развернутые решения примеров на составление уравнения плоскости, которая проходит через заданную прямую и точку.
Навигация по странице.
- Нахождение уравнения плоскости, проходящей через заданную прямую и заданную точку.
- Примеры составления уравнения плоскости, проходящей через заданную точку и прямую.
- Уравнение плоскости, проходящей через точку и прямую онлайн
- Предупреждение
- Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
- Общее уравнение плоскости : описание, примеры, решение задач
- Общее уравнение плоскости: основные сведения
- Общее уравнение плоскости, проходящей через точку
- Неполное общее уравнение плоскости
- 1.3.2. Аналитическая геометрия в пространстве
- 🔥 Видео
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Нахождение уравнения плоскости, проходящей через заданную прямую и заданную точку.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая a и точка 

Сначала покажем, что существует единственная плоскость, уравнение которой нам требуется составить.
Напомним две аксиомы:
- через три различные точки пространства, не лежащие на одной прямой, проходит единственная плоскость;
- если две различные точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Из этих утверждений следует, что через прямую и не лежащую на ней точку можно провести единственную плоскость. Таким образом, в поставленной нами задаче через прямую a и точку M3 проходит единственная плоскость 
Теперь приступим к нахождению уравнения плоскости, проходящей через заданную прямую a и точку 
Если прямая a задана через указание координат двух различных точек М1 и М2 , лежащих на ней, то наша задача сводится к нахождению уравнения плоскости, проходящей через три заданные точки М1 , М2 и М3 .
Если же прямая a задана иначе, то нам сначала придется найти координаты двух точек М1 и М2 , лежащих на прямой a , а уже после этого записать уравнение плоскости, проходящей через три точки М1 , М2 и М3 , которое и будет искомым уравнением плоскости, проходящей через прямую a и точку М3 .
Разберемся, как найти координаты двух различных точек М1 и М2 , лежащих на заданной прямой a .
В прямоугольной системе координат в пространстве любой прямой линии соответствуют некоторые уравнения прямой в пространстве. Будем считать, что способ задания прямой a в условии задачи позволяет получить ее параметрические уравнения прямой в пространстве вида 




После этого нам останется лишь написать уравнение плоскости, проходящей через три различных и не лежащих на одной прямой точки 


Итак, мы получили уравнение плоскости, проходящей через заданную прямую a и заданную точку М3 , не лежащую на прямой a .
Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

Примеры составления уравнения плоскости, проходящей через заданную точку и прямую.
Покажем решения нескольких примеров, в которых разберем рассмотренный метод нахождения уравнения плоскости, проходящей через заданную прямую и заданную точку.
Начнем с самого простого случая.
Напишите общее уравнение плоскости, которая проходит через координатную прямую Ox и точку 
Возьмем на координатной прямой Ox две различные точки, например, 

Теперь получим уравнение плоскости, проходящей через три точки М1 , М2 и М3 :
Это уравнение является искомым общим уравнением плоскости, проходящей через заданную прямую Ox и точку 

Если известно, что плоскость проходит через заданную точку и заданную прямую, и требуется написать уравнение плоскости в отрезках или нормальное уравнение плоскости, то следует сначала получить общее уравнение заданной плоскости, а от него переходить к уравнению плоскости требуемого вида.
Составьте нормальное уравнение плоскости, которая проходит через прямую 

Сначала напишем общее уравнение заданной плоскости. Для этого найдем координаты двух различных точек, лежащих на прямой 



Теперь мы можем составить общее уравнение прямой, проходящей через точку 

Осталось получить требуемый вид уравнения плоскости, умножив обе части полученного уравнения на нормирующий множитель 

Итак, нахождение уравнения плоскости, проходящей через заданную точку и заданную прямую, упирается в нахождение координат двух различных точек, лежащих на заданной прямой. В этом часто состоит основная сложность при решении подобных задач. В заключении разберем решение примера на составление уравнения плоскости, проходящей через заданную точку и прямую, которую определяют уравнения двух пересекающихся плоскостей.
В прямоугольной системе координат Oxyz задана точка 


Отталкиваясь от заданных уравнений двух пересекающихся плоскостей 

Процесс перехода от уравнений двух плоскостей, пересекающихся по прямой a , к параметрическим уравнениям прямой a подробно описан в статье уравнения прямой – уравнения двух пересекающихся плоскостей. Не будем на этом подробно останавливаться, а запишем лишь итоговый результат 




Таким образом, уравнение плоскости, проходящей через точку 


Видео:Уравнение прямой, проходящей через начало координатСкачать

Уравнение плоскости, проходящей через точку и прямую онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:
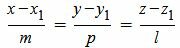 . . | (1) |
Задача заключается в построении уравнения плоскости α, проходящей через точку M0 и и через прямую L(Рис.1).
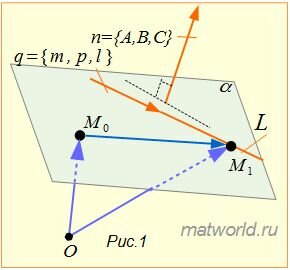 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (3) |
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (5) |
Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M0 и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:
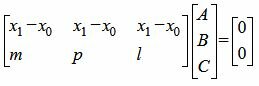 . . | (6) |
Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.
Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.
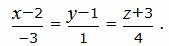 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0)=M0(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (8) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
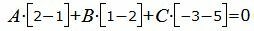 | (10) |
 | (11) |
Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
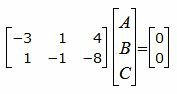 | (12) |
Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:
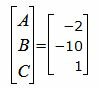 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:
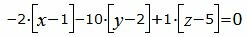 | (13) |
Упростим уравнение (13):
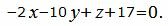 | (14) |
Ответ: Уравнение плоскости, проходящей через точку M0(1, 2, 5) и через прямую (7) имеет вид (14).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и через прямую L, заданной параметрическим уравнением:
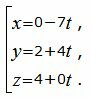 | (15) |
Решение. Приведем параметрическое уравнение (15) к каноническому виду:
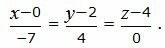 | (16) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (17) |
Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (18) |
Вычитая уравнение (18) из уравнения (17), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (19) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :
| Am+Bp+Cl=0. | (20) |
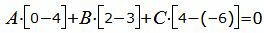 | (21) |
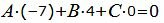 | (22) |
Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
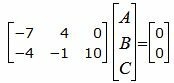 | (23) |
Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:
 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:
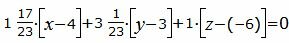 | (24) |
Упростим уравнение (24):
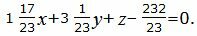 | (25) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.
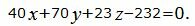 | (26) |
Ответ: Уравнение плоскости, проходящей через точку M0(4, 3, −6) и через прямую (16) имеет вид (26).
Видео:Уравнение плоскости через 3 точкиСкачать

Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )
Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.
Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
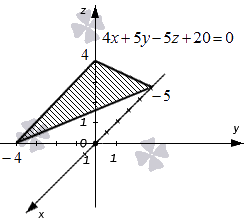
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Общее уравнение плоскости, проходящей через точку
Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.
Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0
Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.
Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:
2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0
Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:
λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0
Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0
3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0
- Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:
M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0
Ответ: 3 x + 7 y — 5 z — 26 = 0
Видео:Уравнение прямой проходящей через начало координат 7 - 8 клСкачать

Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
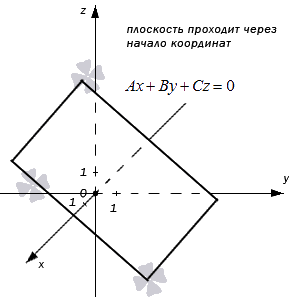
- В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
- Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.
- При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0
Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0
Ответ: x — 7 = 0
Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .
Решение
Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .
Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

1.3.2. Аналитическая геометрия в пространстве
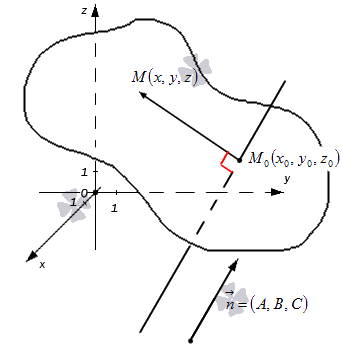
1. Всякая плоскость в координатном пространстве OXYZ имеет векторное уравнение следующего вида: r ¦ п = p. Здесь
r = xi + yj + zk — радиус-вектор текущей точки плоскости
M(x, у, z); п = i cosa + j cos b + k cosg — единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат, a, b, g — углы, образованные этим перпендикуляром с осями координат OX, OY, OZ, и р — длина этого перпендикуляра.
При переходе к координатам это уравнение принимает вид xcos a + ycos b + zcos g — p = 0 (нормальное уравнение плоскости).
2. Уравнение всякой плоскости может быть записано также в виде Ах + Ву +Cz + D = 0 (общее уравнение). Здесь А, B, C можно рассматривать как координаты некоторого вектора
N = Ai + Bj + Ck, перпендикулярного к плоскости. Для приведения общего уравнения плоскости к нормальному виду все члены уравнения надо умножить на нормирующий множитель
где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.
3. Частные случаи расположения плоскости, определяемой уравнением Ах + Ву +Cz + D = 0:
А = 0; плоскость параллельна оси ОХ;
В = 0; плоскость параллельна оси О^
C = 0; плоскость параллельна оси ОZ;
D = 0; плоскость проходит через начало координат;
А = В = 0; плоскость перпендикулярна оси ОZ (параллельна плоскости ХОY);
А = C = 0; плоскость перпендикулярна оси ОY (параллельна плоскости ХОZ);
В = C = 0; плоскость перпендикулярна оси ОХ (параллельна плоскости YОZ);
А = D = 0; плоскость проходит через ось ОХ;
В = D = 0; плоскость проходит через ось OY;
C = D = 0; плоскость проходит через ось OZ;
А = В = D = 0; плоскость совпадает с плоскостью XOY (z = 0);
А = C = D = 0; плоскость совпадает с плоскостью XOZ (у = 0);
B = C = D = 0; плоскость совпадает с плоскостью YOZ (х = 0).
Если в общем уравнении Ах + By +Cz + D = 0 коэффициент D ф 0, то, разделив все члены уравнения на — D, можно уравнение
плоскости привести к виду
. Это уравнение плоскости называется уравнением в отрезках: в нем а — абсцисса точки пересечения плоскости с осью OX, b и с — соответственно ордината и аппликата точек пересечения плоскости с осями OY и OZ.
4. Угол j между плоскостями А1х + В1У + Qz + D1 = 0 и А2х + В2У +C2z + D2 = 0 определяется по формуле
Условие параллельности плоскостей:
Условие перпендикулярности плоскостей:
5. Расстояние от точки М0(х0; у0; z0) до плоскости, определяемой уравнением
Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки M0 и начала координат относительно данной плоскости: этот знак положителен, если точка M0 и начало координат расположены по разные стороны от плоскости, и отрицателен, если они расположены по одну сторону от плоскости.
6. Уравнение плоскости, проходящей через точку М0(х0; у0; z0)
и перпендикулярной к вектору N = Ai + Bj + Ck, имеет вид А(х — х0) + B(y — у0) + C(z — z0) = 0. При произвольных А, В и C последнее уравнение определяет некоторую плоскость, принадлежащую к связке плоскостей, проходящих через точку М0. Его часто поэтому называют уравнением связки плоскостей.
7. Уравнение А1х + B1y +C1z + D1 + А(А2х + B^y +C2z + D2) = 0 при произвольном I определяет некоторую плоскость, проходящую через прямую, по которой пересекаются плоскости, определяемые уравнениями
некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями I и II, параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.
8. Уравнение плоскости, проходящей через три заданные точки M1(r 1Х M1(Jj), M3(r 3) (Л = x1i + yd + z1k; r2 = x2i + У2 j + z2k; r3 = x3i + y3 j + z3 к), проще всего найти из условия компланарности векторов r — T1, r2 — rl, r3 — rl, где r = xi + yj+zk — радиус-вектор текущей точки искомой плоскости M:
или в координатной форме:
Пример 1.21. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + у + 5z — 1 = 0, 2x + 3у — z + 2 = 0 и через точку М(3, 2, 1).
Решение. Воспользуемся уравнением пучка плоскостей
Значение I определяем из условия, что координаты точки М должны удовлетворять этому уравнению:
Получаем искомое уравнение в виде:
или, умножая на 13 и приводя подобные члены, в виде:
Пример 1.22. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + 3у + 5z — 4 = 0 и X — у — 2z + 7 = 0 и параллельной оси оу.
Решение. Воспользуемся уравнением пучка x + 3у + 5z — 4 + + l(x — у — 2z + 7) = 0, преобразуем уравнение к виду (1 + Х)х + (3 -1)у + (5 — 2l)z + (71 — 4) = 0.
Так как искомая плоскость параллельна оси ординат, то коэффициент при у должен равняться нулю, т. е. 3 — l = 0, I = 3. Подставив значение I в уравнение пучка, получаем
Пример 1.23. Найти уравнение плоскости, проходящей через точки М (2; -1; 4) и N(3; 2; -1) перпендикулярно к плоскости X + у + z — 3 = 0.
Решение. Воспользуемся уравнением плоскости, проходящей через первую из данных точек:
Условие прохождения этой плоскости через вторую точку и условие перпендикулярности определяются равенствами:
Исключая коэффициенты А, В и C из системы уравнений
получаем искомое уравнение в виде:
Пример 1.24. Из точки P(2; 3; -5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, будут следующие точки М1(2; 3; 0), М2(2; 0; -5), М3(0; 3; -5). Напишем уравнение плоскости, проходящей через точки М1, М2, М3, для чего воспользуемся уравнением
Пример 1.25. Составить уравнение плоскости, проходящей через точку M (2; 3; 5) и перпендикулярной к вектору
Решение. Достаточно воспользоваться уравнением плоскости, проходящей через данную точку и перпендикулярной к данному вектору:
1. Прямая может быть задана уравнениями 2-х плоскостей
пересекающихся по этой прямой.
2. Исключив поочередно х и у из предыдущих уравнений, получим уравнения х = аz + с, у = bz + d. Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости хoz и yoz.
3. Если даны две точки M(x1, у1, z1) и N(x2, у2, z2), то уравнения прямой, проходящей через них, будут иметь вид:
4. Так называемые канонические уравнения
определяют прямую, проходящую через точку M(x1, у1, z1)
и параллельную вектору S = li + mj + nk. В частности, эти уравнения могут быть записаны в виде:
где a, b и g — углы, образованные прямой с осями координат.
5. От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям прямой:
6. Угол между двумя прямыми, заданными их каноническими

деляется по формуле
перпендикулярности двух прямых:
условие параллельности двух прямых:
7. Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):
Если величины /1, т, П1 непропорциональны величинам /2, m2, «2, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.
условие параллельности прямой и плоскости: 



9. Для определения точки пересечения прямой

а) если А/ + Вт + Cn ф 0, то прямая пересекает плоскость в одной точке;
б) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D ф 0, то прямая параллельна плоскости;
в) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D = 0, то прямая лежит в плоскости.
Пример 1.26. Привести к каноническому виду уравнения прямой 2х — у + 3z — 1 = 0 и 5х + 4у — z — 7 = 0.
Решение. Исключив вначале у, а затем z, получим:
Если разрешим каждое из уравнений относительно х, то будем иметь:
отсюда
Второй способ: найдем вектор S = li + mj + nk, параллельный искомой прямой. Так как он должен быть перпендикулярен к нормальным векторам заданных плоскостей N1 = 2i — j + 3k и N2= 5i + 4 j — k, то за него можно принять векторное произведение векторов N1 и N2.
Таким образом, l = -11; m = 17; n = 13.
За точку M1(x1, у1, z1), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью yoz. Т ак как при этом x1 = 0, то координаты y1 и z1 этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:
Решая эту систему, находим у1 = 2; z1 = 1.
Итак, искомая прямая определяется уравнениями:
Мы получили прежний ответ.
Пример 1.27. Построить прямую
Решение. Искомую прямую можно построить как линию пересечения плоскостей. Для этого напишем уравнения плоскостей, которыми определена прямая, в отрезках на осях:
Пример 1.28. Из начала координат опустить перпендикуляр на прямую
Решение. Составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой: 2х + 3у + z = 0. (Для этой плоскости можно принять А = l; B = m; C = n; D = 0; использовано условие перпендикулярности прямой и плоскости, см. п. 8 введения к настоящему разделу).
Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой имеют вид:
Построив данные плоскости, мы получим искомую прямую как линию пересечения этих плоскостей (рис. 20).
Для определения t имеем уравнение:
Остается составить уравнения прямой, проходящей через начало координат и через точку М (см. п. 3 введения к настоящему разделу):
Пример 1.29. В уравнениях прямой
параметр n так, чтобы эта прямая пересекалась с прямой

Решение. Для нахождения параметра n используем условие пересечения 2-х прямых:
Следовательно, уравнения пересекающихся прямых таковы: искомой:
Для вычисления координат точки пересечения этих прямых выразим из первого уравнения х и у через z: х = 2z, у = -3z. Подставляя их значения в равенство

отсюда z = 1. Зная z, находим х и у: х = 2z = 2, у = -3z = -3. Следовательно M(2; -3; 1).
Пример 1.30. Прямая задана каноническими уравнениями
Составить общие уравнения этой прямой.
Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:
Получили общие уравнения прямой, которая теперь задана пересечением 2-х плоскостей, одна из которых 5х — 3у — 13 = 0 параллельна оси Oz, а другая х + 3z — 11 = 0 параллельна оси Oy.
Пример 1.31. Найти координаты точки M, делящей попалам отрезок прямой
заключенный между плоскостями хoz и xoy.
Решение. Найдем точку А пересечения прямой с плоскостью хoz, полагая в уравнениях прямой у = 0. Тогда получим:
отсюда x = 2,6; z = 2,8. Тогда А(2,6; 0; 2,8).
отсюда X = 11, у = 14, или В(11; 14; 0).
Определяем координаты точки М, делящей отрезок АВ пополам:
Следовательно, координаты искомой точки М будут: М(6,8; 7; 1,4).
Пример 1.32. Составить уравнение плоскости, проходящей через прямую
Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:
которое делим на а ф 0, и пусть b /а = I:
Аналогично, полагая в уравнениях прямой z = 0, найдем координаты точки В пересечения прямой с плоскостью хоу:
В этом пучке нужно выбрать плоскость, параллельную 2-й данной прямой. Из условия параллельности плоскости и прямой, имеем:
Подставляя I = 1 в уравнение пучка плоскостей, получим: 
Пример 1.33. Дана прямая 
Решение. Нужно найти плоскость, которая проходит через данную прямую перпендикулярно к данной плоскости; тогда искомая проекция определится как пересечение этой плоскости с данной.
Составим уравнение пучка плоскостей, проходящих через данную прямую:
Эта плоскость должна быть перпендикулярной к данной плоскости, что можно записать как:
Тогда уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости, будет:
Проекция данной прямой на данную плоскость определяется как прямая пересечения плоскостей:
Запишем эту прямую в каноническом виде. Найдем на прямой какую-либо точку. Для этого положим, например х0 = 1, и система запишется в виде:
Отсюда, у0 = 1, z0 = 0, т. е. точка M(1; 1; 0) принадлежит искомой прямой.
Направляющий вектор прямой S = (l; m; n) найдем из того условия, что он перпендикулярен нормальным векторам
N1 = (2; -3; -2) и N2 = (5; 2; 2) плоскостей, определяющих искомую прямую.
В качестве S берем векторное произведение векторов N1 и N2 , т. е.
Тогда искомое уравнение в каноническом виде будет:
🔥 Видео
Расстояние от точки до прямой (метод координат)Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

5. Нормальное уравнение плоскости выводСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Видеоурок "Нормальное уравнение плоскости"Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

2. Уравнение плоскости примеры решения задач #1Скачать