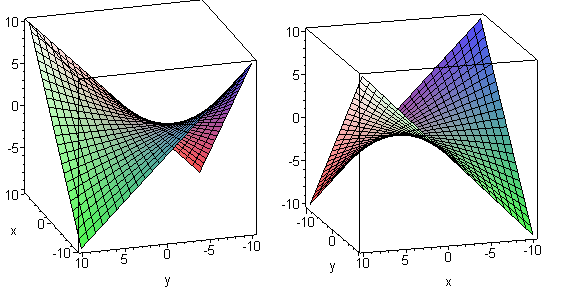
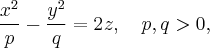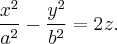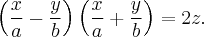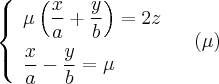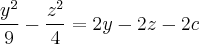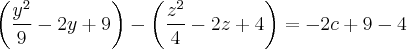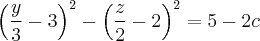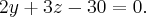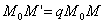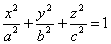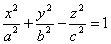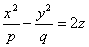Найти уравнение плоскости пересекающей гиперболоид по паре прямых проходящих через точку (6 видео)

Содержание

Прямолинейные образующие на поверхности гиперболического параболоида
Найти уравнение плоскости пересекающей гиперболоид по паре прямых проходящих через точку
Глава 46. Поверхности второго порядка
Однополостный гиперболоид, его каноническое уравнение; прямолинейные образующие. Однополостный гиперболоид вращения.
📹 Видео

Видео:17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Прямолинейные образующие на поверхности гиперболического параболоида

Рассмотрим уравнение гиперболического параболоида:

для удобства сделаем замену и Тогда уравнение запишется в виде

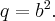
Разложим на множители:

Аналогично с предварительными соображениями получаем уравнения двух семей прямолинейных образующих гиперболического параболоида:

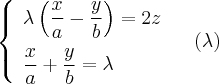
Теорема. На поверхности гиперболического параболоида лежат две семьи прямых, которые имеют следующие свойства:

· через любую точку гиперболического параболоида проходит ровно одна прямая с каждой семьи ;

· любые две образующие из разных семей пересекаются;

· любые две прямые с одной семьи является скрещивающимися;

· любые три прямые с одной семьи параллельные некоторой плоскости.

Доказательство можно посмотреть в методичке.

Пример. Найдите уравнение плоскости, параллельной плоскости и пересекает гиперболический параболоид по двум прямолинейным образующим. Найдите канонические уравнения этих образующих.

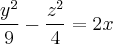
Запишем уравнение параллельной плоскости 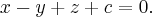Найдем ее пересечение с гиперболическим параболоидом.

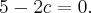
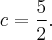
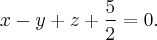
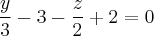
Эта кривая второго порядка распадается на пару прямых, которые пересекаются, если есть Итак плоскость, которую мы ищем, имеет уравнение Две прямые, лежат в этой плоскости и является пересечением с параболоидом:

или 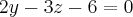и

Уравнения этих прямых в пространстве:

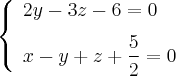
Найдем канонические уравнения. Для первой прямой:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Найти уравнение плоскости пересекающей гиперболоид по паре прямых проходящих через точку

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Глава 46. Поверхности второго порядка

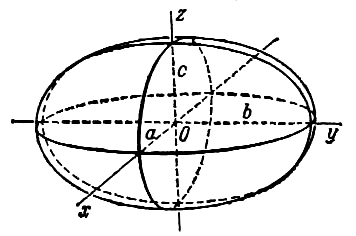
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

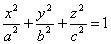
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

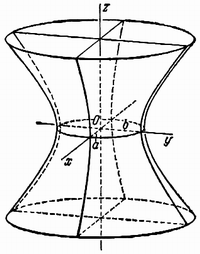
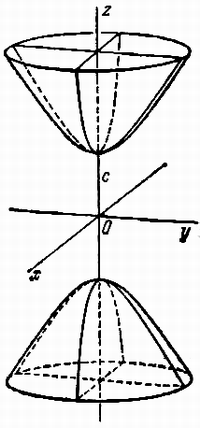
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

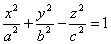
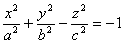
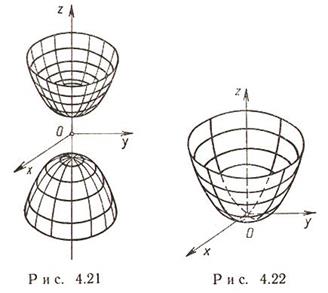
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

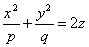
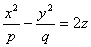
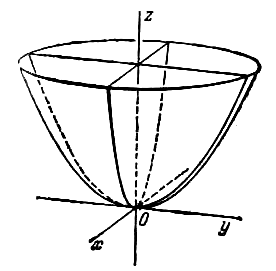
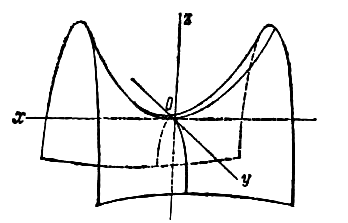
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

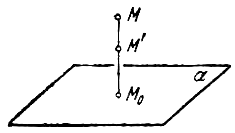
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

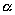
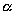
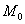
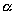
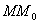
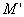
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

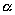
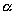
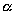
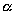
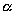
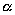
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .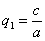

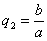
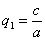
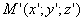
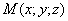
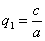
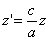
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

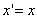
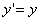
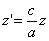
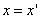
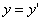
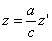
Предположим, что M(x; y; z ) — произвольная точка сферы

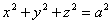
Заменим здесь x, y, z их выражениями (7); получим

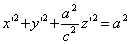
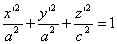
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

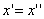
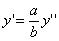
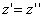
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

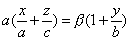
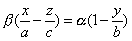
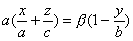
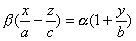
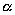
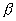
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

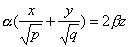
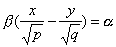
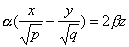
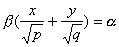
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

Однополостный гиперболоид, его каноническое уравнение; прямолинейные образующие. Однополостный гиперболоид вращения.

однополосный гиперболоид x 2 /a 2 + y 2 /b 2 — z 2 /c 2 =1 a>0,b>0,c>0; Пересек. координатные осиплоскостями x=0,y=0,z=0 по гиперболам y 2 /b 2 – z 2 /c 2 = 1 x 2 /a 2 – z 2 /c 2 =1 и эллипсоид x 2 /a 2 + y 2 /b 2 =1 соответственно. В сечениях однополосного гиперболоида плоскостями z=h всегда получаются эллипсы x 2 /a 2 + y 2 /b 2 = 1 + h 2 /c 2 с полуосями и .

Каноническое уравнение:

a = b — однополостный гиперболоид вращения вокруг оси Oz.

Горловой эллипс:

Асимптотический конус:

Сечения однополостного гиперболоида плоскостями — либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).

Прямолинейные образующие

Через произвольную точку проходят две прямолинейные образующие с направляющими векторами и где:

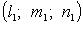
В частности, если точку выбирать на горловом эллипсе то уравнениями прямолинейных образующих будут:

Двуполостный гиперболоид, его каноническое уравнение.

двуполостный гиперболоид x 2 /a 2 — y 2 /b 2 — z 2 /c 2 =1 a>0,b>0,c>0; x=h получается эллипс x 2 /a 2 + z 2 /b 2 = -1 + h 2 /c 2 с полуосями b*Корень(h 2 /a 2 -1) и с*Корень(h 2 /a 2 -1). При h=a получим в сечении точки (±а,0,0) – вершины двуполостного. В сечениях координ пл. z=0 и y=0 получим гиперболы x 2 /a 2 – y 2 /b 2 =1 и x 2 /a 2 – z 2 /c 2 =1 соответсвенно.

Каноническое уравнение:

a = b — двуполостный гиперболоид вращения вокруг оси Oz.

Асимптотический конус:

Сечения двуполостного гиперболоида плоскостями: либо эллипс, либо гипербола, либо парабола, либо точка, либо .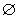

Эллиптический параболоид, его каноническое уравнение.

эллиптический параболоид x 2 /a 2 + y 2 /b 2 =2pz a>0,b>0;

Каноническое уравнение:

p = q — параболоид вращения вокруг оси Oz.

Сечения эллиптического параболоида плоскостями — либо эллипс, либо парабола, либо точка, либо .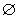

Гиперболический параболоид, его каноническое уравнение. Семейства прямолинейных образующих гиперболического параболоида.

гиперболический параболоид x 2 /a 2 — y 2 /b 2 =2pz a>0,b>0;

Сечения гиперболического параболоида плоскостями — либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие

Через каждую точку проходят две прямолинейные образующие:

Найти уравнение плоскости пересекающей гиперболоид по паре прямых проходящих через точку

Поверхности вращения.

Поверхностью вращения называется поверхность, образованная вращением какой-либо плоской линии вокруг прямой, лежащей в плоскости этой линии.

Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей.

Пусть в координатной плоскости Oyz задана кривая L уравнением F(Y, Z)=0 (рис. 24). Вращаем кривую L вокруг оси Oy. Получим некоторую поверхность. Пусть M(x, y, z) — произвольная точка получившейся поверхности. Тогда
, но т.к. если взять точку M₁ с отрицательной аппликатой, то

Следовательно, имеем Y = y, 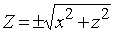и координаты точки M(x, y, z) удовлетворяют уравнению

Уравнение (62) и есть искомое уравнение поверхности вращения.

Т. о., чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскости Oyz, вокруг оси Oy, нужно в уравнении этой линии заменить z на

Аналогичные правила будут иметь место и по отношению к уравнениям поверхностей, полученных вращением плоских линий вокруг других координатных осей.

Цилиндры.

цилиндры второго порядка: эллиптический цилиндр x 2 /a 2 + y 2 /b 2 = 1 a>0, b>0; гиперболический цилиндр x 2 /a 2 — y 2 /b 2 = 1 a>0, b>0; параболический цилиндр y 2 =2px; пара пересекающихся плоскостей a2x2-b2y2=0 a>0 b>0 пара параллельных или совпадающих плоскостей x-a=0 a>=0; прямая x 2 +y 2 =0

Конусы.

конус второго порядка x 2 /a 2 — y 2 /b 2 — z 2 /c 2 =0 a>0,b>0,c>0; Пересекая пл. z=h -> x 2 /a 2 + y 2 /b 2 =1. В сечении плоскостями x=0 y=0 имеем пары пересек прямых y 2 /b 2 — z 2 /c 2 =0; x 2 /a 2 — z 2 /c 2 =0 соотв.