Найти уравнение перпендикуляра к плоскости x 2y z 9 0 проходящего через точку

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Задача 22245 5. Найти уравнения перпендикуляра к.

Условие

5. Найти уравнения перпендикуляра к плоскости x-2y+z-9 = 0, проходящего через точку А(-2;0; -1), и определить координаты основания этого перпендикуляра.

Решение

Нормальный вектор плоскости, является направляющим вектором этого перпендикуляра.
vector=(A;B;C)=(1;-2;1)

Уравнение прямой, проходящей через точку с заданным направляющим вектором (p;q;r):

Находим координаты точки Р — основания перпендикуляра или точки пересечения прямой и плоскjсти
<x-2y+z-9=0
<(x+2)/1=(y-0)/(-2)=(z+1)/1

и подставляем в первое
х-2*(-2х-4)+(х+1)-9=0
6х=0
х=0
y=-2*0 — 4 = — 4
z=0 + 2= 2

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Записать уравнение перпендикуляра к плоскости x + 2y + z — 9 = 0 проходящую через точку С( — 2, 0, — 1) и определить координаты основания этого перпендикуляра?

Математика | 10 — 11 классы

Записать уравнение перпендикуляра к плоскости x + 2y + z — 9 = 0 проходящую через точку С( — 2, 0, — 1) и определить координаты основания этого перпендикуляра.

Записать уравнение перпендикуляра к плоскости x + 2y + z — 9 = 0 проходящего через точку С( — 2, 0, — 1) и определить координаты основания этого перпендикуляра

уравнение перпендикуляра к плоскости x + 2y + z — 9 = 0 проходящего через точку С( — 2, 0, — 1)

прямая параллельна вектору N =

(x + 2) / 1 = (y — 0) / 2 = (z + 1) / 1 = t

координаты основания этого перпендикуляра — координаты точки пересечения прямой (x + 2) / 1 = (y — 0) / 2 = (z + 1) / 1 = t и плоскости x + 2y + z — 9 = 0

(t — 2) + 2(2t) + (t — 1) — 9 = 0

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Прямая проходящая через основания перпендикуляра и наклонной называется?

Прямая проходящая через основания перпендикуляра и наклонной называется.

Видео:Составляем уравнение прямой по точкамСкачать

Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен 60 градусов?

Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен 60 градусов.

Найдите наклонную и ее проекцию на данную плоскость, если перпендикуляр равен 12 см.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Может ли наклонная быть короче перпендикуляра, проведенного из той же точки к той же плоскости?

Может ли наклонная быть короче перпендикуляра, проведенного из той же точки к той же плоскости?

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Если из точки, лежайщей вне плоскости, провести к ней перпендикуляр и на колонные, то?

Если из точки, лежайщей вне плоскости, провести к ней перпендикуляр и на колонные, то?

Видео:Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Из точки к плоскости проведены перпендикуляр и наклонная ?

Из точки к плоскости проведены перпендикуляр и наклонная .

Длина наклонной равна 25 см а длина перпендикуляра проведенного к плоскости 10 см.

Найти длину проектированы наклонной на данную плоскость.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Перпендикуляр к плоскости равен 16 см?

Перпендикуляр к плоскости равен 16 см.

Найти наклонную и ее проекцию на плоскость, если угол между наклонной и перпендикуляром равен 60 градусов.

Видео:Уравнение прямой на плоскости. Решение задачСкачать

Составь уравнение перпендикуляра к прямой 5 х — 3 у + 7 = 0, проходящий через точку ( — 1 ; 3)?

Составь уравнение перпендикуляра к прямой 5 х — 3 у + 7 = 0, проходящий через точку ( — 1 ; 3).

Видео:Как найти проекцию точки на прямую. Линейная алгебраСкачать

Из точки а(6 ; 8)координатной плоскости опущен Перпендикуляр на Ось абцисс?

Из точки а(6 ; 8)координатной плоскости опущен Перпендикуляр на Ось абцисс.

Найдите абциссу основания перпендикуляра.

Видео:Уравнение плоскости через точку и нормальСкачать

Решите пожалуйста срочно В конусе из центра основания к образующей проведен перпендикуляр, который наклонен к плоскости основания под углом α?

Решите пожалуйста срочно В конусе из центра основания к образующей проведен перпендикуляр, который наклонен к плоскости основания под углом α.

Найти площадь полной поверхности конуса, если длина перпендикуляра равна а.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

К плоскости треугольника abc (угол c = 90°) через середину гипотенузы проведен перпендикуляр OM?

К плоскости треугольника abc (угол c = 90°) через середину гипотенузы проведен перпендикуляр OM.

Из точки М опустите перпендикуляры на катеты треугольника.

Вы открыли страницу вопроса Записать уравнение перпендикуляра к плоскости x + 2y + z — 9 = 0 проходящую через точку С( — 2, 0, — 1) и определить координаты основания этого перпендикуляра?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

1 часть — взрослые4 части — дети1 + 4 = 5 (частей) — всего10 : 5 = 2(чел) — приходится на одну часть2 * 4 = 8 (детей)Ответ : 8 детей поехало на экскурсиюили через х : Х (чел) — взрослые4х (чел) — детих + 4х = 105х = 10х = 22 * 4 = 8.

Видео:Прямая на плоскости. Проекция точки на прямуюСкачать

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

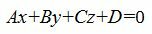(1)

где n(A,B,C)− называется нормальным вектором плоскости.

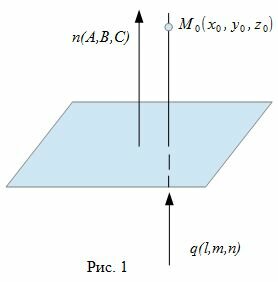
Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

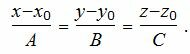(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

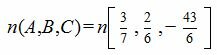(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

📹 Видео

Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

8. Плоскость решение задачСкачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать