Найти уравнение парной регрессии онлайн

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 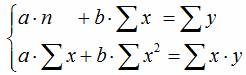. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

МНК и регрессионный анализ Онлайн + графики

Данный онлайн-сервис позволяет найти с помощью метода наименьших квадратов уравнения линейной, квадратичной, гиперболической, степенной, логарифмической, показательной, экспоненциальной регрессии и др., коэффициенты и индексы корреляции и детерминации. Показываются диаграмма рассеяние и график уравнения регрессии. Также калькулятор делает оценку значимости параметров уравнения регрессии с помощью F-критерия Фишера, t-критерия Стьюдента и критерия Дарбина-Уотсона.

Можно задать уровень значимости и указать, до какого знака после запятой округлять расчётные величины.

Примечание: дробные числа записывайте через точку, а не запятую.

Линейная регрессия
Степенная регрессия
Квадратичная регрессия
Кубическая регрессия

Гиперболическая регрессия
Показательная регрессия
Логарифмическая регрессия
Экспоненциальная регрессия

Очистить

Округлять до
-го
знака после запятой.

Калькулятор линейной регрессии

Инструкции: Выполните регрессионный анализ с помощью Калькулятор линейной регрессии , где будет найдено уравнение регрессии и будет предоставлен подробный отчет о расчетах вместе с диаграммой рассеяния. Все, что вам нужно сделать, это ввести данные X и Y. При желании вы можете добавить заголовок и имя переменных.

Подробнее об этом калькуляторе линейной регрессии

А модель линейной регрессии соответствует модели линейной регрессии, которая минимизирует сумму квадратов ошибок для набора пар ((X_i, Y_i)).

Уравнение линейной регрессии, также известное как уравнение наименьших квадратов, имеет следующую форму: (hat Y = a + b X), где коэффициенты регрессии (a) и (b) вычисляются этим калькулятором регрессии следующим образом:

[b = frac<SS_><SS_>] [a = bar Y — bar X cdot b ]

Коэффициент (b) известен как коэффициент наклона, а коэффициент (a) известен как пересечение оси y.

Если вместо линейной модели вы хотите использовать нелинейную модель, вам следует рассмотреть возможность использования калькулятор полиномиальной регрессии , что позволяет использовать степени независимой переменной.

Калькулятор линейной регрессии Шаги

Шаги для проведения регрессионного анализа:

(1) Получите данные для зависимой и независимой переменных в формате столбца.

(2) Введите данные в формате, разделенном запятыми или пробелами.

(3) Нажмите «Рассчитать».

Остатки регрессии

Как мы можем оценить, насколько хороша модель линейной регрессии? Вы можете подумать «легко, просто посмотрите на диаграмма рассеяния «. На самом деле математика и статистика имеют тенденцию выходить за рамки того, где глаз встречается с графиком. Обычно рискованно полагаться только на диаграмму рассеяния для оценки качества модели.

С точки зрения качества соответствия один из способов оценки качества соответствия модели линейной регрессии состоит в следующем: вычисление коэффициента детерминации , указывает долю вариации зависимой переменной, которая объясняется независимой переменной.

В линейной регрессии выполнение допущений имеет решающее значение, поэтому оценки коэффициента регрессии имеют хорошие свойства (среди прочего, несмещенность, минимальная дисперсия).

Чтобы оценить предположения линейной регрессии, вам нужно будет взглянуть на остатки. Для этого вы можете взглянуть на наши калькулятор остатка .

Другие калькуляторы, относящиеся к линейной регрессии

Вас также может заинтересовать вычисление коэффициента корреляции , или в построить диаграмму рассеяния с предоставленными данными.

🎥 Видео