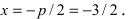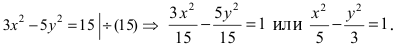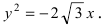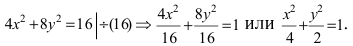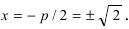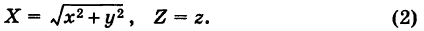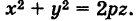Видео:Как легко составить уравнение параболы из графикаСкачать

Глава 20. Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
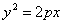
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
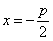
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле
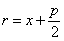
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
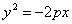
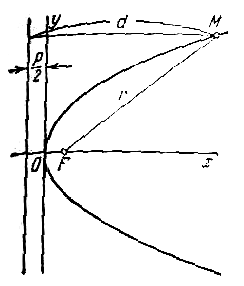
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
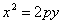
если она лежит в верхней полуплоскости (рис.), и
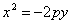
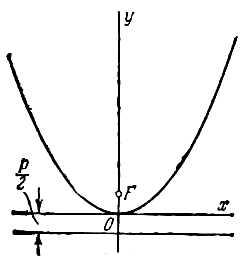
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
Видео:213. Фокус и директриса параболы.Скачать

Парабола — определение и вычисление с примерами решения
Парабола:
Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.
Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы
Рис. 34. Парабола, (уравнение директрисы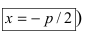
Возведем обе части уравнения в квадрат
Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: 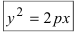
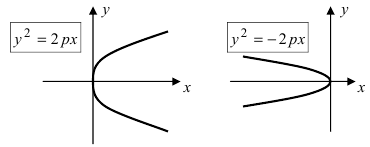
Рис. 35а. Параболы и их уравнения.
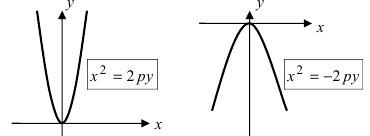
Рис. 356. Параболы и их уравнения.
Найдем координаты точек пересечения параболы с координатными осями:
— точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью ординат.
Определение: Точка О(0; 0) называется вершиной параболы.
Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка 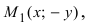
Пример:
Дано уравнение параболы 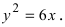
Решение:
Так как из уравнения параболы 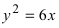
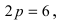
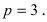
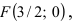
Пример:
Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы 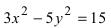
Решение:
Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.
Гипербола:
Следовательно, действительная полуось гиперболы 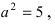
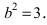
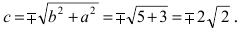
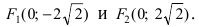
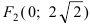
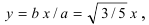
Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:
Пример:
Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса 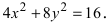
Решение:
Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса 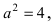
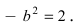
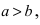
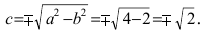
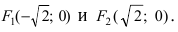
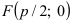
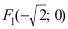
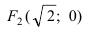

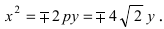
Видео:Фокус и директриса параболы 1Скачать

Уравнение параболоида вращения
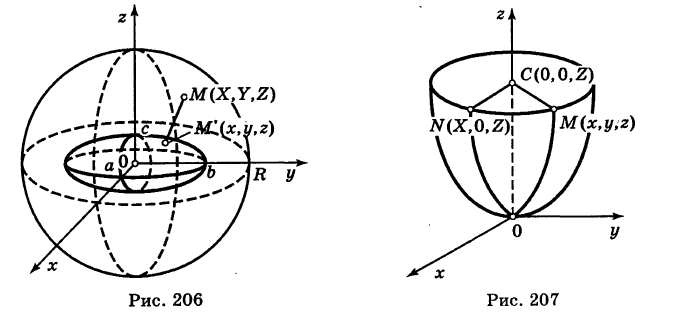
Пусть вертикальная парабола
расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).
Для вывода уравнения поверхности рассмотрим произвольную точку 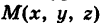
Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем
Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения
Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Многогранники
- Окружность
- Эллипс
- Гипербола
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:§24 Каноническое уравнение параболыСкачать

Парабола: формулы, примеры решения задач
Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы имеет вид:

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.
На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.
В математическом анализе принята другая запись уравнения параболы:
то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.
Фокус параболы имеет координаты
Директриса параболы определяется уравнением 
Расстояние r от любой точки 

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.
Пример 1. Определить координаты фокуса параболы
Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:
Находим координаты фокуса параболы:
Пример 2. Составить уравнение директрисы параболы
Решение. Находим p:
Получаем уравнение директрисы параболы:
Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.
Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:
Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.
Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.
🌟 Видео
Фокус и директриса параболы 2Скачать

Построение параболы по ее директрисе и фокусуСкачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать

Фокус и директриса параболы 2Скачать

Фокус и директриса параболы 1Скачать

Как определить уравнение параболы по графику?Скачать

§25 Исследование канонического уравнения параболыСкачать

Видеоурок "Парабола"Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Параболы. ПримерСкачать

Уравнение параболы #алгебра #графики #парабола #репетиторСкачать

Вычисление фокуса параболыСкачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Как написать уравнение параболы с помощью графикаСкачать

КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать



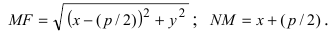
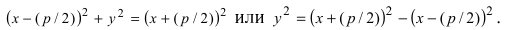
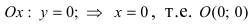 — точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью абсцисс;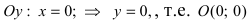 — точка пересечения параболы с осью ординат.
— точка пересечения параболы с осью ординат.