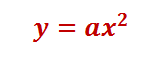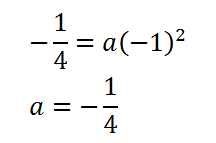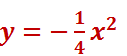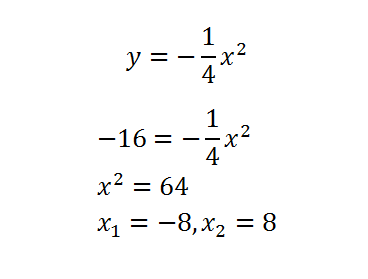Найти уравнение параболы с вершиной в начале координат и проходящей через точку (8 видео)

Найти уравнение параболы с вершиной в начале координат и проходящей через точку

Содержание

Глава 20. Парабола
Известно, что парабола проходит через точку B(-1; -1/4)
Известно, что парабола проходит через точку B(-1; -1/4)
Найти уравнение параболы с вершиной в начале координат и проходящей через точку
🎥 Видео

Видео:Известно, что парабола проходит через точку В(-1; -1/40, и её вершина находится в начале координатСкачать

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

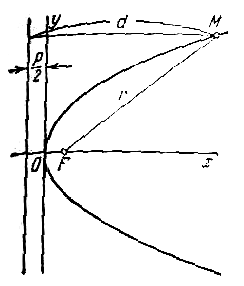
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

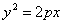
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

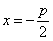
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

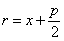
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

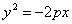
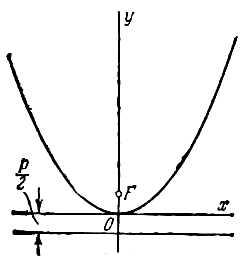
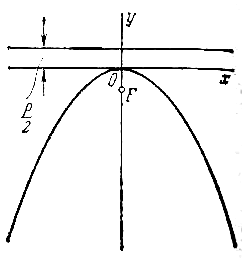
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

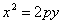
если она лежит в верхней полуплоскости (рис.), и

(4)

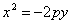
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Известно, что парабола проходит через точку B(-1; -1/4)

Видео:Как легко составить уравнение параболы из графикаСкачать

Известно, что парабола проходит через точку B(-1; -1/4)

Известно, что парабола проходит через точку B(-1; -1/4), и её вершина находится в начале координат,
Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую y = -16

Поскольку вершина параболы лежит в начале координат, то уравнение параболы имеет вид

Найдем значение коэффициента a.

Для этого в уравнение подставим координаты точки B(-1; -1/4)

Уравнение параболы имеет вид

Так как прямая пересекает параболу, следовательно, парабола проходит через точки с ординатой 16.

Подставив в уравнение значение ординаты, найдем абсциссы точек.

Ответ: 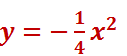(-8; -16), (8; -16)

Смотрите видеоурок с решением задачи.

Видео:Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

Найти уравнение параболы с вершиной в начале координат и проходящей через точку

Парабола симметрична относительно оси Ox, проходит через точку A(4, -1), а вершина ее лежит в начале координат. Составить ее уравнение.

Так как парабола проходит через точку A(4, -1) с положительной абсциссой, а ее осью служит ось Ox, то уравнение параболы следует искать в виде y 2 = 2px. Подставляя в это уравнение координаты точки A, будем иметь