Здравствуйте! Продолжаем рассматривать задачи входящие в состав экзамена по математике. Задания, которые мы рассмотрим ниже, по-большому счёту, никаких глубоких знаний теории не требуют. Для их решения необходимо понимание геометрического смысла производной , умение решать квадратное уравнение и немного логики.
Суть заданий следующая: дана парабола вида у = ах 2 +bх+c и касательная к этой параболе у=kх+b. Один из коэффициентов (a, b или c) неизвестен и его необходимо найти.
Как решать такие задачи? Что необходимо вспомнить?
1. Если даны уравнения двух функций, то точка (точки) пересечения их графиков находится путём решения системы этих уравнений. Пара (х;у) являющаяся решением системы есть точка пересечения графиков (или пары, если точек пересечения больше).
2. Если к графику функции проведена касательная, то производная этой функции в точке касания равна угловому коэффициенту этой касательной (см. ссылку выше).
Рассмотрим задачи (показаны два способа решения):
Прямая у=х+7 является касательной к графику функции ах 2 –15х+15. Найдите a.
Прямая и график данной функции имеют одну общую точку, это значит, что данные уравнения можно внести для решения в одну систему, но этих уравнений будет недостаточно для решения (кроме неизвестных х и у имеется ещё параметр а).
Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(xo) = k. Это третье уравнение, запишем систему:
Подставим из второго уравнения в первое:
Найдём а, подставим х = 1 в ах 2 – 15х + 15 = х + 7 или в 2ах – 15 = 1
По смыслу задачи параметр a ≠ 0, график заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение ах 2 – 15х + 15 = х + 7 имело единственно решение:
Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:
Прямая у=3х+1 является касательной к графику функции ах 2 +2х+3. Найдите a.
Прямая у=5х–8 является касательной к графику функции 6х 2 + bх + 16
Найдите b, учитывая, что абсцисса точки касания больше 0.
Прямая и парабола пересекаются в одной точке, поэтому оба уравнения можно внести в систему, но она не решаема, так как имеем три неизвестных:
Известно, что производная функции в данной точке равна угловому коэффициенту касательной у = kх + b (где k это угловой коэффициент), то есть f′(x o ) = k. Это третье уравнение, запишем систему:
Кратко можно сказать так:
Условия касания графика функции f (x) = k и прямой у = kх + b задаётся системой требований:
По условию, абсцисса точки касания положительна, значит х = 2.
График заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение
имело единственно решение. Преобразуем:
Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:
Теперь определим, при каком значении b абсцисса точки касания будет больше нуля. Можно подставить поочерёдно полученные значения в систему:
Далее решить её и сдать вывод. Верным решением будет то значение b, при котором получим положительную абсциссу.
Но мы сразу подставим их (поочерёдно) в 28х 2 + (b – 5) + 24 = 0.
Таким образом, b = – 19 (при этом значении абсцисса точки касания положительна).
Прямая у = –5х+8 является касательной к графику функции 28х 2 + bх + 15.
Найдите b, учитывая, что абсцисса точки касания больше 0.
Прямая у=–6х–2 является касательной к графику ф-ии 18х 2 +6х+с. Найдите c.
Условия касания графика функции у = f (x) и прямой у = kx + b задаётся системой требований:
График заданной функции — парабола. Прямая с параболой имеет единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение 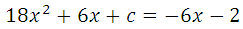

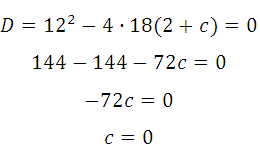
Прямая у=3х+4 является касательной к графику функции 3х 2 –3х+с. Найдите c.
Как видим, понимание способа нахождения точки пересечения графиков функций, заключающееся в решении системы, пригодилось при решении указанных задач (на ЕГЭ могут быть и другие). Но какие бы они не были, если чётко уясните геометрический смысл производной, проблем с подобными у вас не будет.
В данной рубрике продолжим рассматривать задачи, не пропустите!
Имеется круглая мишень радиуса R. На ней отмечены две окружности, радиусы которых равны 1/3 и 2/3 от радиуса мишени. Какова вероятность того, что кинутый в мишень дротик попадёт в закрашенную часть мишени? Результат округлите до тысячных.
*Учесть, что дротик мимо мишени попасть не может.
Тот учащийся, который первый напишет верный ответ, получит поощрительный приз в размере 150 рублей 😉
Надеюсь материал был вам полезен. Успехов Вам!
- Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
- Касательная к графикам функции в точке
- Основные значения угла наклона прямой
- Значение производной функции в точке и ее геометрический смысл
- Понятие уравнения касательной прямой
- Изучение свойств треугольников, вписанных в параболу
- Выполнил:
- ученик 11 класса
- ГУО«Речицкий районный лицей»
- 🌟 Видео
Видео:Составляем уравнение прямой по точкамСкачать

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Время чтения: 30 минут
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Касательная к графикам функции в точке
Угол наклона прямой линии [y=k x+b] — это угол [a], который берет свой отсчет от положительного направления оси координат ox по направлению к прямой. Угол наклона может иметь значение как со знаком плюс, так и со знаком минус.
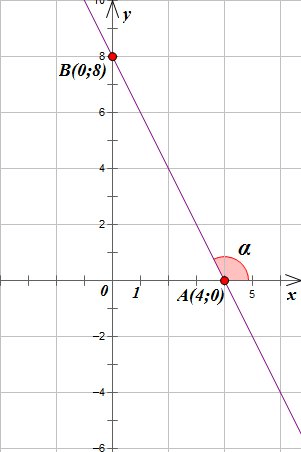
На расположенном рис.1 показана прямая и угол наклона относительно оси.
Для каждого угла наклона характерен угловой коэффициент прямой.
Угловой коэффициент — это числовой коэффициент прямой вида [boldsymbol]. В уравнение он обозначается буквой k.
Угловой коэффициент равен значению тангенса наклона заданной прямой линии: [k=operatorname alpha].
Видео:Как легко составить уравнение параболы из графикаСкачать

Основные значения угла наклона прямой
- Угол наклона прямой линии будет иметь нулевое значение, только в случае, когда параллельна ось Ox, и значение углового коэффициента равняется нулю. Потому что [operatorname 0=0]. Следовательно уравнение прямой будет записываться следующим образом: [y=b].
- В случае, когда угол наклона будет острым, то должно выполняться два следующих условия: [0 0]. При этом будет наблюдаться возрастание графика функции на протяжении всей координатной прямой.
- При условии, что угол [alpha=frac], из этого следует, что прямая будет располагаться относительно оси Ox в перпендикулярном положении. Условие задается следующим равенством [x=c]. Где с — это простое действительное число.
- Если угол наклона прямой, является тупым, то будет применяться следующее условие: [frac
Рисунок 2. Секущая прямая на графике функции.
На графике показана секущая, которая обозначена красным цветом и точками А и В.
Если угловой коэффициент прямой линии равен тангенсу угла наклона, то используя прямоугольный треугольник можно найти значение тангенса. Сделать это можно вычислением по правилу: тангенс равен отношению противолежащего катета к прилежащему.
Чтобы определить значение секущий, нужно использовать следующую формулу:
Значение секущий определяется, используя следующее неравенство:
Уравнение записывается следующим образом:
Касательная к графику функции — это прямая, которая проходит через определенную заданную точку, которая в свою очередь имеет отрезок с множеством числовых значений x.
Пример:
Прямая задана следующей функцией: [y=x+1]. Данная функция считается касательной к графику [y=2 sqrt] с координатными точками (1;2).
Рассмотрим графики со значениями (1;2). Функция обозначается черным цветом, а касательная линия соответственно синим цветом.
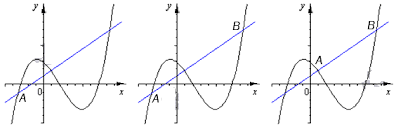
Чтобы определить касательную к функции, нужно исследовать поведение касательной АВ. При этом должно быть бесконечное приближение точки В к точке А.
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Значение производной функции в точке и ее геометрический смысл
Для заданной функции [f(chi)] рассмотрим секущую АВ. Точки А и В заданы следующими значениями: [left(chi_, fleft(chi_right)right)] и [left(chi_+Delta chi ,left(chi_+Delta chiright)right.].
[Delta chi] — это показатель приращения значения аргумента.
Подставив все значения в исходную функцию получим следующий вид:
[Delta y=Delta f(chi)=fleft(chi_+Delta chiright)-f(Delta chi)].
Для более лучшего восприятия решения, построим график.
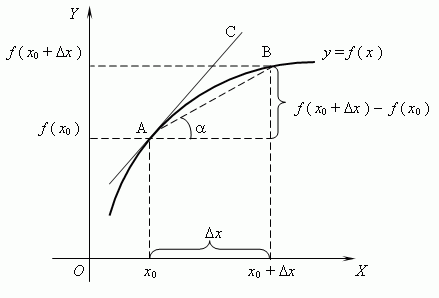
Из графика видно, что образуется прямоугольный треугольник ABC. Составим соотношение [frac=operatorname alpha], для этого необходимо применить основное определение тригонометрической функции, а именно тангенса.
Исходя из основного определения касательной, запишем следующее выражение:
Используя правило производной, имеем следующее:
- производная [f(x)] в точке [x_] — является пределом отношения приращения функции к аргументу.
- [Delta_ rightarrow 0 text fleft(x_right)=lim _ frac].
[k_] — это угловой коэффициент касательной функции.
Из данной функции можно сделать следующий вывод:
- функция [f(x)] может находится в точке со значением [x_]
- функция может быть касательной к графику в некой точке касания, где угловой коэффициент равняется производной.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Понятие уравнения касательной прямой
Чтобы составить уравнение прямой, нужно знать угловой коэффициент с заданной точкой. Это точка, через которую проходит прямая. При пересечении угловой коэффициент записывается как значение [x_].
Уравнение касательной записывается следующим образом:
График функции [y=f(x)].
Расположение касательной прямой непосредственно зависит от значения углового коэффициента. Если прямая параллельна оси Ox, то значение коэффициента равно нулевому значению. При параллельном расположении относительно оси Oy, коэффициент угловой принимает значение бесконечности. При это уравнение касательной записывается как: [x=x_].Также угловой коэффициент будет возрастать при значении больше нуля, а если коэффициент меньше нуля, то функция соответственно будет убывать.
Нужно составить уравнение касательной к графику функции.
Порядок решения: Из условия задачи следует, что функция может быть определенной для всех действительных значений. Точка, которая задана с координатами (1;3) будет являться точкой касания, следовательно , [x_=-1, fleft(x_right)=-3].
Для точки со значение равным -1, нужно определить производную. Для этого составим уравнение:
Показатель [f^(x)] в точке, которая является касательной, будет равен угловому коэффициенту.
Угловой коэффициент равен наклону тангенса. Отсюда следует, что:
Подведем итоги, и запишем ответ:
По условию задачи нужно определить касательную к графику функции [y=3 cdot sqrt[5]+1]. Точки координат равны (1;1). Также нужно составить уравнение и определить значение угла наклона. Согласно условию задачи, область определения функции — это простые действительные числа. Определим значение производной.
При условии, что [x_=1] тогда функция будет не определенной, но пределы ее можно записать как:
Это значит, что вертикальная касательная в точке существует.
Ответ: после всех проведенных вычислений уравнение приобретает вид x=1, где угол наклона будет равен [frac].
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Изучение свойств треугольников, вписанных в параболу
Научно-практическая конференция учащихся и педагогов
«Первые шаги в науку»
Изучение свойств треугольников, вписанных в параболу
Выполнил:
ученик 11 класса
ГУО«Речицкий районный лицей»
ГУО«Речицкий районный лицей»
2. Парабола и аналитическая геометрия……………………………………. 6
3. Парабола и треугольник……………………………………………………. 8
4. Об одном свойстве параболы………………………………………………..11
В школьной программе заметное место уделяется построению графиков функций. Моя работа посвящена изучению параболы. Я думаю, она будет интересна и поучительна всем тем, кто увлечен таким предметом, как математика. Линию такую как парабола, мы изучали в 8 классе. В курсе аналитической геометрии, она имеет другую формулу и график. Свойства, которые я буду исследовать, найдут применение в различных предметах. Исследование начинается с элементарных фактов и заканчивается весьма удивительными вещами. В своей работе я буду наблюдать за параболой, около которой будет описан или в которую вписан треугольник. А также рассмотрю интересные задачи олимпиадного уровня. В основном упор будет делаться на задачи с треугольниками, так как там можно увидеть интересные вещи, которые могут быть исследованы в других работах. Тема моей исследовательской работы актуальна и может быть полезна школьникам старших классов, учителям, а также учащимся физико-математического направления, и просто тем, кто увлечен математикой.
1. Парабола в алгебре
Парабола – это график квадратичной функции вида y=ax2+bx+c. Ее также можно представить видом 
(m, n) ее можно определить:

🌟 Видео
Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Уравнение окружности (1)Скачать

Найти координаты пересечения параболы и прямойСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

213. Фокус и директриса параболы.Скачать

§24 Каноническое уравнение параболыСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

найти уравнение касательной к эллипсуСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Фокус и директриса параболы 1Скачать

Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Уравнение окружностиСкачать



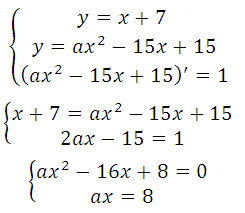
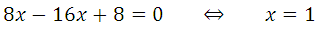
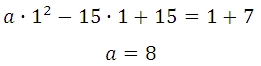
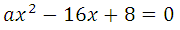
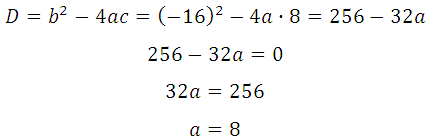
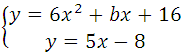
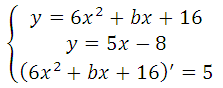
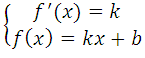
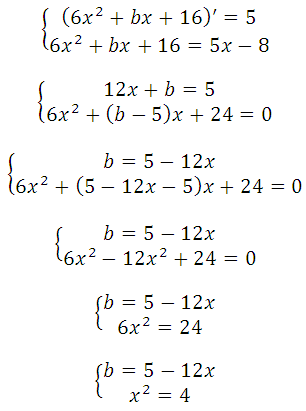
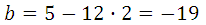
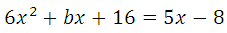
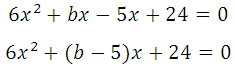
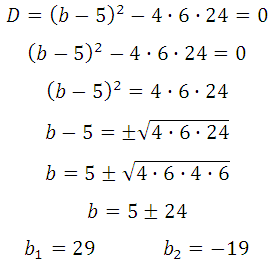
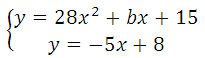
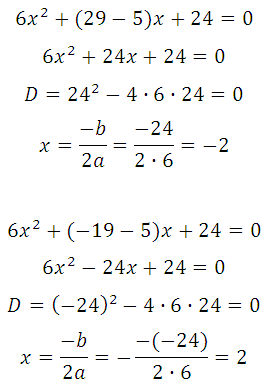
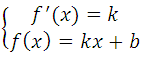
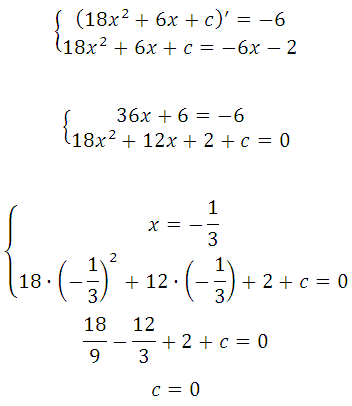

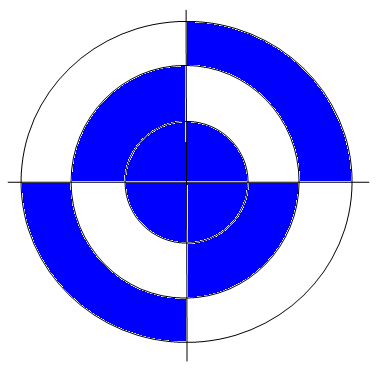
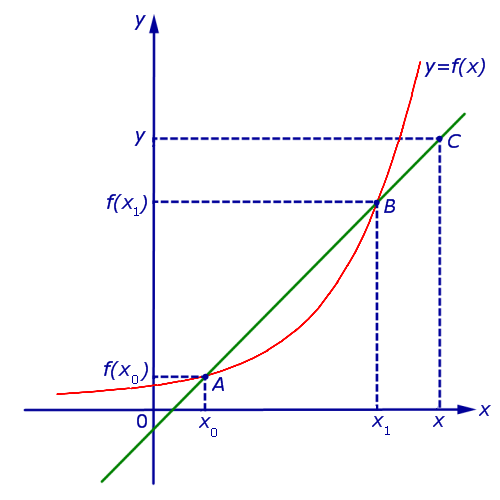 Рисунок 2. Секущая прямая на графике функции.
Рисунок 2. Секущая прямая на графике функции.