- Информация о задаче
- Условие задачи
- Решение
- Геометрическое применение производной: уравнения касательной и нормали, угол между кривыми
- Касательная и нормаль к кривой
- Угол между кривыми
- Решение задач по математике онлайн
- Калькулятор онлайн. Уравнение прямой касательной к графику функции в заданной точке
- Немного теории.
- Угловой коэффициент прямой
- Уравнение касательной к графику функции
- 💥 Видео
Видео:Математика без Ху!ни. Уравнение касательной.Скачать
Информация о задаче
Задача №2457 параграфа №1 главы №8 «Применения интеграла» книги Г.Н. Бермана «Сборник задач по курсу математического анализа» (22-е издание, 2002 год).
Видео:Как написать уравнения касательной и нормали | МатематикаСкачать
Условие задачи
Вычислить площадь фигуры, ограниченной параболой [math]y^2=2px[/math] и нормалью у ней, наклонённой к оси абсцисс под углом [math]135^[/math] .
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Решение
Для определённости полагаем [math]pgt[/math] , что вполне соответствует знаку параметра в каноническом уравнении параболы. Обозначим [math]f(x,y)=y^2-2px[/math] , тогда получим:
Пусть нормаль проведена в точке [math](x_0;y_0)[/math] . Угловой коэффициент нормали: [math]k=-frac=-frac
[/math] . Так как угловой коэффициент прямой равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс, т.е. [math]k=tg<135^>=-1[/math] , то получим:
Так как [math]y_0=p[/math] , то [math]x_0=frac<y_^>=frac
[/math] . Нормаль проведена в точке [math]left(frac
;pright)[/math] . Уравнение нормали будет таким:
[dmath] y-p=-1cdotleft(x-frac
right);; x=-y+frac. [/dmath]
Найдём точки пересечения нормали и параболы:
Решая данную систему, мы придём к уравнению [math]y^2+2py-3p^2=0[/math] , откуда получим [math]y_1=p[/math] , [math]y_2=-3p[/math] . Таким образом, нормаль пересекает параболу в точках [math]left(frac
;pright)[/math] и [math]left(frac;-3pright)[/math] .
Видео:§24 Каноническое уравнение параболыСкачать
Геометрическое применение производной: уравнения касательной и нормали, угол между кривыми
Видео:Как определить уравнение параболы по графику?Скачать
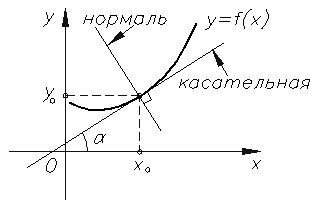
Касательная и нормаль к кривой
Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.
Если кривая определена уравнением $y=f(x)$, то уравнение касательной к ней в точке $M(x_0;y_0)$ имеет вид:
а уравнение нормали:
Задание. Написать уравнение касательной и нормали к кривой $y=x^2-3x+4$ в точке с абсциссой $x_0=0$.
Решение. Находим значение функции в заданной точке:
Далее вычислим значение производной функции в точке $x_0=0$:
а тогда уравнение касательной запишется в виде:
или после упрощения:
$$y-4=-frac(x-0) Rightarrow x-3 y+12=0$$
Ответ. Уравнение касательной: $3x+y-4=0$
Уравнение нормали: $x-3y+12=0$
Видео:Уравнения касательной и нормали к кривойСкачать
Угол между кривыми
Углом между кривыми на плоскости в их общей точке $M(x_0;y_0)$ называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым $y=f_1(x)$ и $y=f_2(x)$, соответственно $y=k_x+b_$ и $y=k_x+b_2$, то тангенс угла между кривыми определяется соотношением:
Задание. Найти тангенс угла между кривыми $y=x^2-1$ и $y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.
Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:
Таким образом, искомая точка $x=1$.
Далее находим производные заданных функций в найденной точке:
Итак, искомый тангенс:
Ответ. $operatorname phi=frac$
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать
Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке
Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем точке ( x_0 ).
Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).
Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> Введите выражение функции ( f(x)) и число (x_0) — абсциссу точки в которой нужно построить касательную Найти уравнение касательной
Видео:Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать
Немного теории.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Угловой коэффициент прямой
Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом прямой, а угол ( alpha ) — углом между этой прямой и осью Ox
Видео:Видеоурок "Парабола"Скачать
Уравнение касательной к графику функции
Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.
Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.
С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное равенство: (f(a)=ka+b ), т.е. ( b = f(a) — ka ).
Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:
Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).
Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )
💥 Видео
КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать
3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать
Как легко составить уравнение параболы из графикаСкачать
213. Фокус и директриса параболы.Скачать
Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать
Уравнение касательнойСкачать
УРАВНЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИСкачать
Как записать уравнение нормали к кривой в точке экстремумаСкачать
Уравнение окружности (1)Скачать
