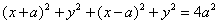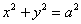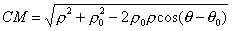Найти уравнение множества точек для каждой из которых сумма расстояний

Видео:18. Расстояние от точки до прямой в пространствеСкачать

Задача 43842 Составить уравнение множества точек, для.

Условие

Составить уравнение множества точек, для каждой из которых выполняется следующее условие: сумма квадратов расстояний до точек A(1,1) и B (-3,3) равна 20

Все решения

Упрощаем, раскрываем скобки:

Выделим полные квадраты:

(x+1)^2+(y-2)^2=5 — уравнение окружности с центром в точке (-1;2)
R=sqrt(5)

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Найти уравнение множества точек, для каждой из которых сумма расстояний от двух точек F₁(4 ; 0) и F₂( — 4 ; 0) равна 10?

Найти уравнение множества точек, для каждой из которых сумма расстояний от двух точек F₁(4 ; 0) и F₂( — 4 ; 0) равна 10.

Эллипс—геометрическое место точекM, для которых сумма расстояний до двух данных точекF₁ и F₂(называемыхфокусами) постоянна и больше расстояния между фокусами.

По условию F₁M + F₂M = 10.

Так как фокусные расстояния F₁ и F₂ равноудалены от начала координат, то центр эллипса лежит в начале координат.

Каноническое уравнение эллипса : х² / а² + у² / b² = 1.

Расположим точку М на оси Oy, тогда b = MO.

MO — высота равнобедренного треугольника F₁MF₂.

F₁M + F₂M = 10, значит F₁M = 5.

В треугольнике ОМF₁ MO² = F₁M² — OF₁² = 5² — 4² = 9,

Расположим точку М на оси Oх, тогда а = МО.

2F₁M = 10 — F₂F₁ = 10 — 8 = 2,

a = MO = OF₁ + F₁M = 4 + 1 = 5.

Итак, уравнение нашего эллипса :

х² / 25 + у² / 9 = 1 — это ответ.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Найти все углы которые образовались при пересечении двух прямых если сумма двух из них равна 320°?

Найти все углы которые образовались при пересечении двух прямых если сумма двух из них равна 320°.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Помогите мне пожалуйста :Задайте на алгебраическом языке и изобразите на координатной плоскости множество точек, у которых :В) — абсцисса на 2 больше ординатыГ) — сумма абсциссы и ориднаты равна4Дам 6?

Помогите мне пожалуйста :

Задайте на алгебраическом языке и изобразите на координатной плоскости множество точек, у которых :

В) — абсцисса на 2 больше ординаты

Г) — сумма абсциссы и ориднаты равна4

Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Сколько различных точек на числовой окружности задает указанное множество чисел?

Сколько различных точек на числовой окружности задает указанное множество чисел.

Видео:Множества и операции над нимиСкачать

Составьте уравнение линии которой принадлежат все точки такие что разность квадратов расстояний от них до точек А(1, 0) и В( — 1, 2) равна 1?

Составьте уравнение линии которой принадлежат все точки такие что разность квадратов расстояний от них до точек А(1, 0) и В( — 1, 2) равна 1.

Видео:Алгебра, 8 класс | Множества точек на плоскости. Часть 2Скачать

Сколько сфер можно нарисовать из (через) :а) двух (две) точек (точки) ;б) трех (три) точек (точки)?

Сколько сфер можно нарисовать из (через) :

а) двух (две) точек (точки) ;

б) трех (три) точек (точки)?

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Написать уравнение множества точек, для каждой из которых модуль разности расстояний от точек F₁(4 ; 0) и F₂( — 4 ; 0) равен 6?

Написать уравнение множества точек, для каждой из которых модуль разности расстояний от точек F₁(4 ; 0) и F₂( — 4 ; 0) равен 6.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Постройте множество всех точек удаленных от точки А на расстоянии 2 см , а от точки В на расстоянии 1, 5 см , если АВ = 3см ?

Постройте множество всех точек удаленных от точки А на расстоянии 2 см , а от точки В на расстоянии 1, 5 см , если АВ = 3см .

Видео:ГМТ // ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕКСкачать

Даны точки А ( — 5 ; 1) и В ( 3 ; 5)?

Даны точки А ( — 5 ; 1) и В ( 3 ; 5).

Составить уравнение множества точек, из которых отрезок АВ виден под прямым углом.

Видео:PRO геометрические места точекСкачать

Докажите что множество всех точек плоскости находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от неё, есть прямая, параллельная данной прямой?

Докажите что множество всех точек плоскости находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от неё, есть прямая, параллельная данной прямой.

Видео:Такие разные бесконечности. Счётные и несчётные множества | матан #005 | Борис Трушин !Скачать

Сколько прямых можно провести через различные пары из : а) 3 точек ; б) 4 точек ; в) 5 точек ; г) * n точек, никакие из которых не принадлежат одной прямой?

Сколько прямых можно провести через различные пары из : а) 3 точек ; б) 4 точек ; в) 5 точек ; г) * n точек, никакие из которых не принадлежат одной прямой?

Если вам необходимо получить ответ на вопрос Найти уравнение множества точек, для каждой из которых сумма расстояний от двух точек F₁(4 ; 0) и F₂( — 4 ; 0) равна 10?, относящийся к уровню подготовки учащихся студенческий, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

BA( — 2 ; — 6) BC( — 9 ; 1) S(ABC) = 1 / 2 * | BA x BC | = 1 / 2 * | ( — 2) * (1) — ( — 9) * ( — 6) | = 1 / 2 * 56 = 28.

Теорема косинусов : Применим для нашего треугольника : , отсюда Складываем и Выражаем m. Что и требовалось доказать.

Решение смотри в файле.

180 — 28 = 152°________________.

A N B M C MN — средняя линия, MN II AB. Средняя линия равна половине стороны, которой она параллельна. Значит AB = 2 * MN = 16 см. Но треугольник ABC — равнобедренный, значит AC = AB = 16см. Периметр — это сумма длин всех сторон, значит : P = AB ..

Pk = (7 + 15) / 2 = 11 h = 66 / 11 = 6 S = (11 + 15) / 2 •6 / 2 = 13•3 = 39.

Складемо ривняння : 10 = 3х + х 10 = 4х х = 2. 5 МА = 7. 5 МВ = 2. 5.

ΔABC — прямоугольный, ∠C = 90° ; AC = 9 ; cos∠A = 1 / 3АВ — гипотенузаОтношения в прямоугольном треугольнике Ответ : АВ = 27.

Вот это правильно shsbbssoow. He sush.

У ромба все стороны равны. Р / 4 = 4 см — одна сторона. В прямоугольном треугольнике сторона, которая лежит напротив угла 30°, равна половине гипотенузы. Когда мы проведем высоту, сторона ромба будет гипотенузой, а высота — её половиной. (4 / 2 =..

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Найти уравнение множества точек для каждой из которых сумма расстояний

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Глава 10. Вывод уравнений заранее данных линий

В задачах предыдущего параграфа линия определялась при помощи данного уравнения. Здесь мы будем иметь задачи противоположного характера; в каждой из них линия определяется чисто геометрически, а уравнение ее требуется найти.

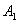
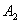
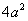
ПРИМЕР 1. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек (-а; 0) и (а; 0) есть величина постоянная, равная .

РЕШЕНИЕ. Обозначим буквой М произвольную точку линии, буквами х и у обозначим координаты этой точки. Так как точка М может занимать на линии любое положение то х и у являются переменными величинами; их называют текущими координатами.

Запишем геометрическое свойство линии символически:

(1).

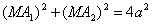
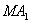
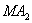
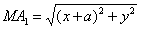
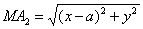
В этом отношении при движении точки М могут меняться длины и . Выразим их через текущие координаты точки М:

, (2)

Подставив полученные выражения в равенство (1), найдем уравнение, связывающее координаты х, у точки М:

Это и есть уравнение данной линии.

Действительно, для каждой точки М, лежающей на этой инии, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на линии, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Однако уравнение (2) можно упростить; раскрывая скобки и приводя подобные члены, получим уравнение данной линии в виде:

Теперь легко понять, что данная линия есть окружность с центром в начале координат и радиусом, равным а.

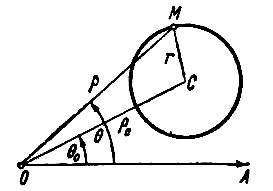
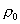
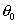
ПРИМЕР 2. В полярной системе координат вывести уравнение окружности, которая имеет центр С( ; ) и радиус r (см. рис.).

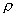
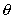
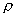
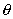
РЕШЕНИЕ. Олозначим буквой М произвольную точку окружности, буквами и — ее полярные координаты. Так как точка М может занимать на окружности любое положение, то и являются переменными величинами. Как и в случае декартовой системы, их называют текущими координатами.

Все точки окружности отстоят от центра на расстоянии r ; запишем это условие символически:

(1).

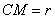
Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов):

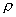
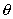
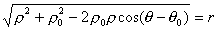
Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты , точки М:

(2)

Это и есть уравнение данной окружности.

Действительно, для каждой точки М, лежащей на данной окружности, выполняется условие (1) и , следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на данной окружности, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Можно лишь несколько упростить полученное уравнение и представить его в виде, свободным от радикала:

.

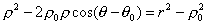
🌟 Видео

Задачи с параметром и расстояние на плоскостиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

2022 11 18 Динамика лекции все для заочников pptxСкачать

Алгоритм ДейкстрыСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать