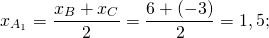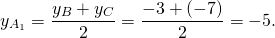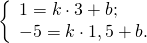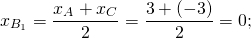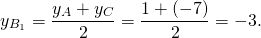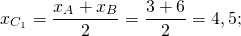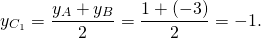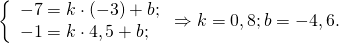Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
Видео:Вычисляем высоту через координаты вершин 1Скачать

Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
Видео:Уравнения стороны треугольника и медианыСкачать

3) Координаты точки C1 — середины отрезка BC:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.
Аналитическая геометрия
Задача 3. Даны вершины треугольника ABC (рис. 1): А(-4,8), В(5,-4), С(10, 6).
1) длину стороны АВ;
2) уравнение высоты СД и ее длину;
Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

3) уравнение медианы, проведенной из вершины А;
4) записать уравнение прямой, проходящей через точку С параллельно стороне АВ.
1. Расстояние d между точками М1(x1у1) и М2(х2у2) определяется по формуле

Подставим в формулу (1) координаты точек А и В, получим
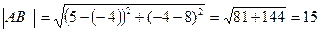
2. Уравнение прямой, проходящей через точки М1(x1у1) и М2(х2у2), имеет вид

Подставив в формулу (2) координаты точек А и В, получим уравнение прямой АВ:
Для нахождения углового коэффициента КАВ прямой АВ разрешим полученное уравнение относительно у: 
Отсюда 


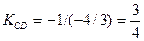
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Искомая высота проходит через точку С(10,6). Воспользуемся уравнением прямой, проходящей через данную точку, с заданным угловым коэффициентом:
Y-6= 
Для нахождения длины СD определим координаты точки D, решив систему уравнений (АВ) и (СD): 
Подставив в формулу (1) координаты точек С и Д, находим
3. Обозначим основание искомой медианы через М. По определению медианы М делит сторону ВС пополам. Координаты точки М найдем по формуле

Чтобы записать уравнение медианы AM, воспользуемся формулой (2). 




4. Обозначим искомую прямую СР. Угловой коэффициент 

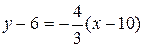


Задача 4. Расходы на автомобильном транспорте выражаются формулой у=120+30х, а на железнодорожном — у=160+20х, где х — расстояние в километрах, у — транспортные расходы на 1 км. (в усл. ден. ед.).
Построить графики функций, произвести экономический анализ, рассчитать транспортные расходы при х=200 км.
1. Построим прямые у=120+30х (I) и у=160+20х (II) (рис. 4).
Рис.4
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Найдем точку пересечения двух прямых



Если х=4, оба вида транспорта эквивалентны по затратам.
Если х 4 выгоднее становятся железнодорожные перевозки.
Рассчитаем транспортные расходы при х=200 км.
у=120+30∙200=6120 (усл. ден. ед.) — затраты на автомобильном
У=160+4000=4150 (усл. ден. ед.) — затраты на железнодорожном транспорте.
🎥 Видео
№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Площадь треугольника ABC равна 36. DE – средняя линия, параллельная стороне AB.Скачать

Уравнение прямой и треугольник. Задача про высотуСкачать

найти уравнение высоты треугольникаСкачать

Длина медианы треугольникаСкачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Построение медианы в треугольникеСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

90 задач по геометрии решается этим способом!Скачать
РАВНЫЕ ТРЕУГОЛЬНИКИ. Высоты. Медианы. Биссектрисы. §7 геометрия 7 классСкачать

8 класс, 25 урок, Средняя линия треугольникаСкачать