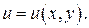Страницы работы
Содержание работы
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
для студентов металлургических специальностей
к выполнению семестрового задания по теме «Теория поля»
с вариантами заданий
Рекомендовано на заседании кафедры высшей математики
Протокол № 4 от 14.02.2002 г.
Утверждено на заседании
Протокол № 8 от 22.04.2002 г.
1 Скалярное поле
Функция U=U(p)=U(x,y,z) называется скалярной, если она характеризуется только числовым значением. Если в каждой точке некоторой области задана скалярная функция U, то говорят, что в этой области задано скалярное поле. Примером скалярного поля может служить поле температур неравномерно нагретого тела, поле плотностей распределения электрических зарядов в изолированном наэлектризованном теле, поле потенциалов электрического поля и т.д.
Скалярное поле может совпадать со всем пространством, если функция U определена в любой точке, или являться некоторой его частью, если функция U определена только в этой части пространства.
Скалярное поле называется стационарным, если функция U=U(p) не зависит от времени t, и называется нестационарным, если такая зависимость функции U от t существует.
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U принимает постоянное значение, т.е.
Видео:Силовые линии и эквипотенциальные поверхностиСкачать

U (x,y,z) = C.
В курсе физики при рассмотрении поля потенциала поверхности уровня называют обычно эквипотенциальными поверхностями (т.е. поверхностями равного потенциала).
Если скалярное поле плоское, т.е. U = U(x,y), то поверхности уровня будут линиями уровня
Уравнение поверхности уровня, проходящей через данную точку M0 (x0,y0,z0) записывается так:
1) Найти линии уровня скалярного поля U = xy
Линии уровня удовлетворяют уравнению:
xy = C или 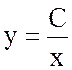
т.е. линиями уровня будет семейство гипербол в 1-й и 3-ей четвертях при C>0 или во 2-й и 4-й четверти при C 1 2 3 4 5 6
Видео:Физика 10 класс (Урок№27 - Напряжённость и потенциал электростатического поля.Разность потенциалов.)Скачать

Типовой расчёт. «Теория поля»
Задача 1. Дано векторное поле
1. Проверить, что это поле является потенциальным.
2. Найти потенциал поля
3. Найти уравнение линий равного потенциала и изобразить линии равного потенциала на чертеже.
4. Составить уравнение векторных линий поля 
5. Вычислить линейный интеграл 
| Вар. | Векторное поле | Точка A | Точка B |
 |  |  | |
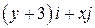 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  | 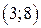 | |
 |  |  | |
 |  |  | |
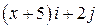 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
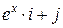 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
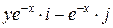 |  |  | |
 |  |  | |
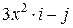 |  |  | |
 |  | 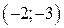 | |
 |  |  | |
 |  |  |
Задача 2. Дано векторное поле 
1. Найти дивергенцию векторного поля 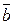
2. Найти поток векторного поля 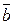

3. Найти ротор векторного поля 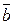
4. Вычислить циркуляцию поля 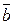


5. Выяснить, как изменится циркуляция поля 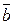

| Вар. | Поле 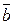 : :  — поверхность, ограничивающая тело Т. — поверхность, ограничивающая тело Т.  — замкнутая линия — замкнутая линия |
   . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами  | |
   . .  состоит из дуги окружности состоит из дуги окружности   и двух отрезков прямых и двух отрезков прямых  и и  , ,  | |
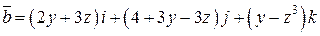   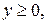  . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
     . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
   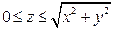 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами  | |
    . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 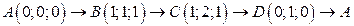 | |
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
   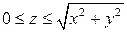 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами  | |
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
   . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
  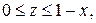 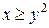 . .  состоит из дуги эллипса состоит из дуги эллипса   и его диаметра и его диаметра  : :  | |
  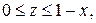   . .  -эллипс -эллипс 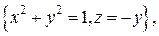 обходимый в направлении обходимый в направлении  | |
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
   . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 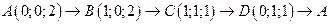 | |
   . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
    . .  состоит из дуги окружности состоит из дуги окружности   и ее диаметра и ее диаметра  : :  | |
  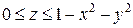 . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 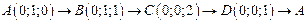 | |
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
    . .  -контур ромба с вершинами -контур ромба с вершинами  | |
    . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами 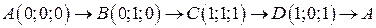 | |
  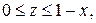   . .  состоит из дуги эллипса состоит из дуги эллипса  : :  и его диаметра и его диаметра  , ,  | |
    . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
   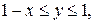  . .  состоит из дуги окружности состоит из дуги окружности   и ее диаметра и ее диаметра  : :  | |
   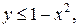  . .  — контур ромба с вершинами — контур ромба с вершинами 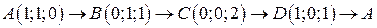 | |
    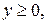  . .  -контур треугольника с вершинами -контур треугольника с вершинами  | |
   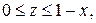   — состоит из дуги окружности — состоит из дуги окружности   и двух отрезков прямых и двух отрезков прямых  и и  : :  | |
   . .  -контур параллелограмма с вершинами -контур параллелограмма с вершинами 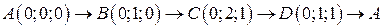 | |
    . .  -контур прямоугольника с вершинами -контур прямоугольника с вершинами  |
Список литературы.
1.Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2, изд.13. – М.:Наука,1985.560 с.
2.Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.- М.:Наука,1989.464 с.
3. Кудрявцев Л.Д.Курс математического анализа Т.1,2. -М.: Высшая школа,1981.614с.;470 с.
4. Гаврилов В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. Учебник для вузов. Под ред. В.С. Зарубина, А.П. Крищенко. Серия «Математика в техническом университете». Вып. VII.- М.:МГТУ,2001.492 с.
5. Осипова М.З. Теория поля. Учебное пособие по выполнению контрольного задания. — М.:МВТУ,1978.
Оглавление.
1. Скалярные и векторные поля. 4
2. Поверхности и линии уровня. 5
3. Производная по направлению скалярного поля. 7
4. Градиент скалярного поля. 9
5. Векторные линии векторного поля. 12
6. Криволинейный интеграл векторного поля. 15
7. Потенциальное векторное поле. 20
8. Поток векторного поля. 28
9. Дивергенция векторного поля. Соленоидальное векторное поле. 32
10. Ротор (вихрь) векторного поля. Формула Стокса. 37
Видео:Поверхности и линии уровняСкачать

Дано векторное поле Проверить что это поле является потенциальным
Дано векторное поле .
Проверить, что это поле является потенциальным.
Найти потенциал поля .
Найти уравнение линий равного потенциала и изобразить линии равного потенциала на чертеже.
Составить уравнение векторных линий поля и изобразить векторные линии на том же чертеже, указав стрелками направление векторных линий.
Вычислить линейный интеграл , , .
Проверим, что данное поле является потенциальным.
Найдем ротор данного поля:
,
.
.
.
.
Отсюда следует, что данное поле является потенциальным.
Найдем потенциал поля .
Найдем потенциал данного поля с помощью криволинейного интеграла:
Найдем уравнение линий равного потенциала и изобразим линии равного потенциала на чертеже.
Линии равного потенциала определяются уравнением:
или ,
.
Изобразим линии равного потенциала на чертеже при нескольких значениях константы ():
Составим уравнение векторных линий поля и изобразим векторные линии на том же чертеже, указав стрелками направление векторных линий.
Векторные линии данного поля определяются дифференциальным уравнением:
.
.
.
Изобразим векторные линии поля на том же чертеже при нескольких значениях константы (), указав стрелками направление векторных линий:
Вычислим линейный интеграл , , .
Поскольку данное поле является потенциальным, то данный интеграл не зависит от пути интегрирования, а определяется разницей значений потенциала в точке и точке :
Видео:9 класс, 5 урок, Уравнение линии на плоскостиСкачать

Исследование электрических полей (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
Видео:Электростатика | эквипотенциальные поверхностиСкачать

Министерство образования Российской Федерации.
Омский Государственный Технический Университет.
Кафедра «Электрической техники»
Исследование электрических полей
Методические указания к лабораторным работам по курсу
Видео:Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Министерство образования Российской Федерации.
Омский Государственный Технический Университет.
Исследование электрических полей.
Методические указания к лабораторным работам.
Видео:Урок 218. Напряженность электрического поляСкачать

Омск 2003
Введение
Данное методическое указание предназначено для помощи студентам при выполнении лабораторных работ по курсу ТОЭ «Исследование электростатических полей». Выполнение работ предусмотрено с использованием персонального компьютера, что позволяет не только рассчитать параметры поля, но и наглядно увидеть графическое представление картины поля, получаемое в ходе лабораторных расчетов.
Курс лабораторных работ рассчитан на выполнение четырех работ по математическому моделированию электрических полей :
— исследование электрического поля двухпроводной линии передачи;
— исследование электрического поля параллельных несоосных цилиндров;
— исследование плоскопараллельного электрического поля между электродами заданной геометрии;
— исследование электрического поля у края плоского конденсатора.
Каждая лабораторная работа содержит несколько обязательных разделов:
2. Краткая теория;
3. Рабочее задание;
4. Домашнее задание;
5. Вопросы к защите.
В первом разделе содержатся задачи, которые должны быть решены студентом в ходе лабораторной работы. В краткой теории изложены основные теоретические положения, используемые для составления и решения конкретной задачи. Раздел рабочее задание содержит указания для выполнения той части работы, в которой используется персональный компьютер. Домашнее задание предлагается студенту для закрепления теоретической базы, а также для расширения знаний по данным вопросам. Выполнение пятого раздела позволяет студенту подготовиться к защите теоретической части лабораторной работы.
Лабораторная работа 1
Исследование электрического поля двухпроводной линии передачи
Цель работы. Математическое моделирование электрического поля двухпроводной линии. Расчет основных величин, характеризующих поле и линию. Исследование влияния расстояния между проводами, радиуса провода на характеристики электрического поля и параметры линии.
Расчетная схема двухпроводной линии передачи приведена на рис.1.
 |
Электрическое поле двухпроводной линии является плоскопараллельным, так как основные величины, характеризующие поле (вектор напряженности электрического поля 

Будем рассматривать плоскость, в которой расположены линии напряженности электрического поля, как плоскость комплексного переменного 



Функция

— есть функция комплексного переменного. Запись (1) означает, что каждому значению чисел 











Поскольку по определению производные для дифференцируемой функции не зависят от пути, по которому производится приближение к точке, то должно выполняться равенство


Эти уравнения называют условиями Коши – Римана. Если продифференцировать первое уравнение в выражении (3) по 




Аналогичным образом, дифференцируя в выражении (3) первое уравнение по 


Уравнения (5) и (6) представляют собой уравнения Лапласа для функций 

Аналитические функции 

Будем считать, что функция 

Тогда для расчета напряженности электрического поля 



С учетом условия Коши – Римана из соотношений (3) следует



Уравнение силовой линии поля в декартовых координатах имеет вид

после подстановки в него составляющих напряженности электрического поля согласно ( 8 ) получим:















где А – действительная постоянная.
Принимая во внимание, что 



Из выражения (12) видно, что действительная и мнимая части функции комплек-сного переменного есть


Линии равного электрического потенциала и линии функции потока в этом случае определяются следующими условиями 





Воспользовавшись теоремой Гаусса нетрудно найти постоянную

где 

Подставляя в (12) постоянную 
Напряженность электрического поля при этом будет

Если две из эквипотенциальных поверхностей такого поля заменить тонкими про-водящими поверхностями с потенциалами 

при 
при 
постоянная 

Подставляя ее выражение в уравнение (11), можно определить комплексный потен-циал поля коаксиального кабеля

Для поля двух линейных зарядов 



где 
Обозначая расстояния от точки 









Линии равного электрического потенциала определяются условием 

Уравнение линии равного потенциала удобнее записывать в декартовых координа-тах

Полученное уравнение — есть уравнение окружности с радиусом 



Координата 


Если принять в выражении (21) 



то есть числа 


 |
Приняв в выражении функции потока 



Рис.2 Построение линии равного электрического потенциала.
Уравнение любой линии напряженности электрического поля имеет вид:


и, следовательно, является уравнением дуги окружности, пересекающейся с линей-ными проводами, что видно непосредственно по рис. 3.
 |
Рис.3 Построение линии напряженности электрического поля.
Действительно, 


Координаты центра окружности


Чтобы подразделить поле на трубки равного потока, следует считать разность 


Провода реальной двухпроводной линии передачи имеют конечные сечения. Пусть 


нетрудно убедится, что 


При этом поле внутри металлических проводов будет отсутствовать, а поле в диэ-лектрике с учетом замены реальных проводов электрически заряженными осями останется без изменения, так как удовлетворяется граничное условие – постоянство потенциала на поверхности провода.
На рис.5 построена картина электрического поля двухпроводной линии пере-дачи, причем принято 



Согласно выражению (15) напряженность электрического поля в точке 

Если принять во внимание притяжение зарядов разного знака, то очевидно, что распределение плотности электрического заряда 
Напряжение между проводами линии с учетом выражения (21) будет:

Емкость двухпроводной линии передачи не зависит от заряда (




1. Открыть окно программы по расчету электрического поля параллельных несоосных цилиндров, запускающий файл программы mkp. exe (рис.4).
Внимание! Программа содержит встроенную помощь и информацию о прог-рамме, которые можно получить нажатием на расположенные в вернем левом углу окна кнопки «Помощь» и «О программе».
Произвести ввод данных по коду (по указанию преподавателя) нажатием на кнопки «Ввод данных» и после завершения ввода кода «Ok».
2. Нажать на кнопку «Решение» и войти в диалоговое окно построения картины электрического поля двухпроводной линии передачи (рис. 5).
Заполнить табл. 1 значениями расчетных параметров K, 

🎬 Видео
Урок 231. Свойства электрического потенциалаСкачать

Урок 233. Задачи на электрический потенциал - 1Скачать

как решать задачи со сложными схемамиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Эквипотенциальные поверхности. Уравнения Пуассона и Лапласа.Скачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

Задача №2. Потенциал проводящей сферы.Скачать

Урок 230. Простейшие задачи на электрический потенциалСкачать

Билет №04 "Потенциал электростатического поля"Скачать

Урок 229. Работа электрического поля. Потенциал. Электрическое напряжениеСкачать

Силовые линии электрического поляСкачать

Кокшаров Ю. А. - Электромагнетизм - Расчет и измерение потенциала электростатического поляСкачать