Найти уравнение линейной регрессии python

Дата публикации Jun 18, 2019

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Введение

Эта статья пытается быть справочной информацией, которая вам нужна, когда дело доходит до понимания и выполнения линейной регрессии. Хотя алгоритм прост, лишь немногие действительно понимают основные принципы.

Во-первых, мы углубимся в теорию линейной регрессии, чтобы понять ее внутреннюю работу. Затем мы реализуем алгоритм на Python для моделирования бизнес-задачи.

Я надеюсь, что эта статья найдет свой путь в ваши закладки! А пока давайте к этому!

Видео:Множественная Линейная Регрессия || Машинное ОбучениеСкачать

Теория

Линейная регрессия, вероятно, является самым простым подходом для статистического обучения. Это хорошая отправная точка для более продвинутых подходов, и фактически многие причудливые статистические методы обучения можно рассматривать как расширение линейной регрессии. Следовательно, понимание этой простой модели создаст хорошую базу, прежде чем перейти к более сложным подходам.

Линейная регрессия очень хороша, чтобы ответить на следующие вопросы:

• Есть ли связь между 2 переменными?
• Насколько прочны отношения?
• Какая переменная вносит наибольший вклад?
• Насколько точно мы можем оценить влияние каждой переменной?
• Насколько точно мы можем предсказать цель?
• Являются ли отношения линейными? (Дух)
• Есть ли эффект взаимодействия?

Видео:Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]Скачать

Оценка коэффициентов

Предположим, у нас есть только одна переменная и одна цель. Тогда линейная регрессия выражается как:

В приведенном выше уравнениибетыявляются коэффициентами. Эти коэффициенты — то, что нам нужно, чтобы делать прогнозы с нашей моделью.

Итак, как мы можем найти эти параметры?

Чтобы найти параметры, нам нужно минимизироватьнаименьших квадратовилисумма квадратов ошибок, Конечно, линейная модель не идеальна, и она не будет точно предсказывать все данные, а это означает, что существует разница между фактическим значением и прогнозом. Ошибка легко вычисляется с помощью:

Но почему ошибки возводятся в квадрат?

Мы возводим в квадрат ошибку, потому что прогноз может быть выше или ниже истинного значения, что приводит к отрицательной или положительной разнице соответственно. Если бы мы не возводили в квадрат ошибки, сумма ошибок могла бы уменьшиться из-за отрицательных различий, а не потому, что модель хорошо подходит.

Кроме того, возведение в квадрат ошибок учитывает большие различия, поэтому минимизация квадратов ошибок «гарантирует» лучшую модель.

Давайте посмотрим на график, чтобы лучше понять.

На приведенном выше графике красные точки — это истинные данные, а синяя линия — линейная модель. Серые линии иллюстрируют ошибки между предсказанными и истинными значениями. Таким образом, синяя линия — это та, которая минимизирует сумму квадратов длины серых линий.

После некоторой математики, которая является слишком тяжелой для этой статьи, вы можете наконец оценить коэффициенты с помощью следующих уравнений:

гдех бара такжеу барпредставляют собой среднее.

Видео:11. Анализ данных на python: линейная регрессияСкачать

Оцените актуальность коэффициентов

Теперь, когда у вас есть коэффициенты, как вы можете определить, актуальны ли они для прогнозирования вашей цели?

Лучший способ — найтир-значение.р-значениеиспользуется для количественной оценки статистической значимости; это позволяет определить, следует ли отклонить нулевую гипотезу или нет.

Для любой задачи моделирования гипотеза состоит в том, чтоесть некоторая корреляциямежду функциями и целью. Таким образом, нулевая гипотеза противоположна:нет корреляциимежду функциями и целью.

Итак, нахождениер-значениедля каждого коэффициента будет указано, является ли переменная статистически значимой для прогнозирования цели. Как правило, еслир-значениеявляетсяменее чем 0,05: между переменной и целью существует тесная связь.

Видео:Решение задачи регрессии | Глубокое обучение на PythonСкачать

Оцените точность модели

Вы обнаружили, что ваша переменная была статистически значимой, найдя еер-значение, Большой!

Теперь, как узнать, хороша ли ваша линейная модель?

Чтобы оценить это, мы обычно используем RSE (остаточная стандартная ошибка) и статистику R².

Первая метрика ошибки проста для понимания: чем меньше остаточных ошибок, тем лучше модель соответствует данным (в этом случае, чем ближе данные к линейной зависимости).

Что касается метрики R², он измеряетдоля изменчивости в цели, которая может быть объяснена с помощью функции X, Следовательно, при условии линейного отношения, если признак X может объяснить (предсказать) цель, тогда пропорция высока, и значение R² будет близко к 1. Если противоположное верно, значение R² будет тогда ближе к 0.

Видео:Множественная линейная регрессия в Python. Машинное обучение ПРОСТО! ПРОГНОЗИРУЕМ ЦЕНУ НЕДВИЖИМОСТИ!Скачать

Теория множественной линейной регрессии

В реальных ситуациях никогда не будет единственной функции, чтобы предсказать цель Итак, выполняем ли мы линейную регрессию по одному объекту за раз? Конечно нет. Мы просто выполняем множественную линейную регрессию.

Уравнение очень похоже на простую линейную регрессию; просто добавьте количество предикторов и соответствующие им коэффициенты:

Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Оцените актуальность предиктора

Ранее в простой линейной регрессии мы оценивали релевантность функции, находя еер-значение,

В случае множественной линейной регрессии мы используем другую метрику: F-статистику.

Здесь F-статистика рассчитывается для всей модели, тогда какр-значениеспецифичен для каждого предиктора. Если существует сильная связь, то F будет намного больше 1. В противном случае она будет приблизительно равна 1.

Какбольшечем 1достаточно большой?

Это сложно ответить. Обычно, если имеется большое количество точек данных, F может быть немного больше 1 и предполагать тесную связь. Для небольших наборов данных значение F должно быть намного больше 1, чтобы предполагать тесную связь.

Почему мы не можем использоватьр-значениев этом случае?

Поскольку мы подгоняем много предикторов, нам нужно рассмотреть случай, когда есть много функций (пбольшой). При очень большом количестве предикторов всегда будет около 5%, у которых, случайнор-значениечетное хотя они не являются статистически значимыми.Поэтому мы используем F-статистику, чтобы не рассматривать неважные предикторы как значимые предикторы.

Видео:РЕАЛИЗАЦИЯ ЛИНЕЙНОЙ РЕГРЕССИИ | Линейная регрессия | LinearRegression | МАШИННОЕ ОБУЧЕНИЕСкачать

Оцените точность модели

Как и в простой линейной регрессии, R² может использоваться для множественной линейной регрессии. Однако знайте, что добавление большего количества предикторов всегда будет увеличивать значение R², потому что модель обязательно будет лучше соответствовать обучающим данным.

Тем не менее, это не означает, что он будет хорошо работать с тестовыми данными (делая прогнозы для неизвестных точек данных).

Видео:ML: пишем на python модель simple linear regression для определения выброса СО2 автомобилемСкачать

Добавление взаимодействия

Наличие нескольких предикторов в линейной модели означает, что некоторые предикторы могут влиять на другие предикторы.

Например, вы хотите предсказать зарплату человека, зная его возраст и количество лет, проведенных в школе. Конечно, чем старше человек, тем больше времени он мог бы проводить в школе. Итак, как мы моделируем этот эффект взаимодействия?

Рассмотрим этот очень простой пример с двумя предикторами:

Как видите, мы просто умножаем оба предиктора вместе и связываем новый коэффициент. Упрощая формулу, мы теперь видим, что на коэффициент влияет значение другого признака.

Как правило, если мы включаем модель взаимодействия, мы должны включать индивидуальный эффект объекта, даже если егор-значениенезначительный. Это известно какиерархический принцип, Это объясняется тем, что если два предиктора взаимодействуют, то включение их индивидуального вклада окажет небольшое влияние на модель.

Хорошо! Теперь, когда мы знаем, как это работает, давайте заставим это работать! Мы будем работать как с простой, так и с множественной линейной регрессией в Python, и я покажу, как оценивать качество параметров и общую модель в обеих ситуациях.

Вы можете получить код и данныеВот,

Я настоятельно рекомендую вам следовать и воссоздать шаги в своем собственном блокноте Jupyter, чтобы в полной мере воспользоваться этим руководством.

Давайте доберемся до этого!

Мы все так кодируем, верно?

Видео:[ОТКРЫТЫЙ КУРС] Python для финансистов - Модуль Statsmodels. Линейная регрессия - Урок 11Скачать

Введение

Набор данных содержит информацию о деньгах, потраченных на рекламу, и их продажах. Деньги были потрачены на рекламу на телевидении, радио и в газетах.

Цель состоит в том, чтобы использовать линейную регрессию, чтобы понять, как расходы на рекламу влияют на продажи.

Видео:Лекция 2.1: Линейная регрессия.Скачать

Импорт библиотек

Преимущество работы с Python заключается в том, что у нас есть доступ ко многим библиотекам, которые позволяют нам быстро читать данные, наносить на график данные и выполнять линейную регрессию.

Мне нравится импортировать все необходимые библиотеки поверх ноутбука, чтобы все было организовано. Импортируйте следующее:

Видео:Лекция 8. Линейная регрессияСкачать

Читать данные

Предполагая, что вы загрузили набор данных, поместите его в data каталог в папке вашего проекта. Затем прочитайте данные так:

Чтобы увидеть, как выглядят данные, мы делаем следующее:

И вы должны увидеть это:

Как видите, столбец Unnamed: 0 избыточно Следовательно, мы удалим это.

Хорошо, наши данные чисты и готовы к линейной регрессии!

Видео:Линейная Регрессия для Дата СаентистаСкачать

Простая линейная регрессия

Видео:13-14 Множественная регрессия в pythonСкачать

моделирование

Для простой линейной регрессии, давайте рассмотрим только влияние телевизионной рекламы на продажи. Прежде чем перейти непосредственно к моделированию, давайте посмотрим, как выглядят данные.

Мы используем matplotlib , популярная библиотека для построения графиков на Python

Запустите эту ячейку кода, и вы должны увидеть этот график:

Как видите, существует четкая взаимосвязь между суммой, потраченной на телевизионную рекламу, и продажами.

Давайте посмотрим, как мы можем сгенерировать линейное приближение этих данных.

Да! Это так просто, чтобы подогнать прямую линию к набору данных и увидеть параметры уравнения. В этом случае мы имеем

Давайте представим, как линия соответствует данным.

И теперь вы видите:

Из приведенного выше графика видно, что простая линейная регрессия может объяснить общее влияние суммы, потраченной на телевизионную рекламу и продажи.

Видео:Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Оценка актуальности модели

Теперь, если вы помните из этогопосле, чтобы увидеть, является ли модель хорошей, нам нужно посмотреть на значение R² ир-значениеот каждого коэффициента.

Вот как мы это делаем:

Что дает вам этот прекрасный вывод:

Глядя на оба коэффициента, мы имеемр-значениеэто очень мало (хотя, вероятно, это не совсем 0). Это означает, что существует сильная корреляция между этими коэффициентами и целью (продажи).

Затем, глядя на значение R², мы получаем 0,612. Следовательно,около 60% изменчивости продаж объясняется суммой, потраченной на телевизионную рекламу, Это нормально, но точно не лучшее, что мы можем точно предсказать продажи. Конечно, расходы на рекламу в газетах и ​​на радио должны оказывать определенное влияние на продажи.

Посмотрим, будет ли лучше работать множественная линейная регрессия.

Видео:Простая Линейная Регрессия || Машинное ОбучениеСкачать

Множественная линейная регрессия

Видео:Занятие 14. Линейная регрессия в Scikit-learnСкачать

моделирование

Как и для простой линейной регрессии, мы определим наши функции и целевую переменную и используемscikit учитьсябиблиотека для выполнения линейной регрессии.

Больше ничего! Из этой ячейки кода мы получаем следующее уравнение:

Конечно, мы не можем визуализировать влияние всех трех сред на продажи, так как оно имеет четыре измерения.

Обратите внимание, что коэффициент для газеты является отрицательным, но также довольно небольшим. Это относится к нашей модели? Давайте посмотрим, рассчитав F-статистику, значение R² ир-значениеза каждый коэффициент.

Видео:15 Линейная регрессияСкачать

Оценка актуальности модели

Как и следовало ожидать, процедура здесь очень похожа на то, что мы делали в простой линейной регрессии.

И вы получите следующее:

Как вы можете видеть, R² намного выше, чем у простой линейной регрессии, со значением0,897!

Кроме того, F-статистика570,3, Это намного больше, чем 1, и поскольку наш набор данных достаточно мал (всего 200 точек),демонстрирует тесную связь между расходами на рекламу и продажами,

Наконец, поскольку у нас есть только три предиктора, мы можем рассмотреть ихр-значениеопределить, имеют ли они отношение к модели или нет. Конечно, вы заметили, что третий коэффициент (для газеты) имеет большойр-значение, Поэтому рекламные расходы на газетуне является статистически значимым, Удаление этого предиктора немного уменьшит значение R², но мы могли бы сделать более точные прогнозы.

Вы качаетесь 🤘. Поздравляю с завершением, теперь вы мастер линейной регрессии!

Как упоминалось выше, это может быть не самый эффективный алгоритм, но он важен для понимания линейной регрессии, поскольку он формирует основу более сложных статистических подходов к обучению.

Я надеюсь, что вы когда-нибудь вернетесь к этой статье.

Видео:Нерепетитор Клуб: линейная регрессия (31.03.2019)Скачать

Python, корреляция и регрессия: часть 2

Предыдущий пост см. здесь.

Видео:Линейная регрессияСкачать

Регрессия

Хотя, возможно, и полезно знать, что две переменные коррелируют, мы не можем использовать лишь одну эту информацию для предсказания веса олимпийских пловцов при наличии данных об их росте или наоборот. При установлении корреляции мы измерили силу и знак связи, но не наклон, т.е. угловой коэффициент. Для генерирования предсказания необходимо знать ожидаемый темп изменения одной переменной при заданном единичном изменении в другой.

Мы хотели бы вывести уравнение, связывающее конкретную величину одной переменной, так называемой независимой переменной, с ожидаемым значением другой, зависимой переменной. Например, если наше линейное уравнение предсказывает вес при заданном росте, то рост является нашей независимой переменной, а вес — зависимой.

Описываемые этими уравнениями линии называются линиями регрессии . Этот Термин был введен британским эрудитом 19-ого века сэром Фрэнсисом Гэлтоном. Он и его студент Карл Пирсон, который вывел коэффициент корреляции, в 19-ом веке разработали большое количество методов, применяемых для изучения линейных связей, которые коллективно стали известны как методы регрессионного анализа.

Вспомним, что из корреляции не следует причинная обусловленность, причем термины «зависимый» и «независимый» не означают никакой неявной причинной обусловленности. Они представляют собой всего лишь имена для входных и выходных математических значений. Классическим примером является крайне положительная корреляция между числом отправленных на тушение пожара пожарных машин и нанесенным пожаром ущербом. Безусловно, отправка пожарных машин на тушение пожара сама по себе не наносит ущерб. Никто не будет советовать сократить число машин, отправляемых на тушение пожара, как способ уменьшения ущерба. В подобных ситуациях мы должны искать дополнительную переменную, которая была бы связана с другими переменными причинной связью и объясняла корреляцию между ними. В данном примере это может быть размер пожара. Такие скрытые причины называются спутывающими переменными, потому что они искажают нашу возможность определять связь между зависимыми переменными.

Линейные уравнения

Две переменные, которые мы можем обозначить как x и y, могут быть связаны друг с другом строго или нестрого. Самая простая связь между независимой переменной x и зависимой переменной y является прямолинейной, которая выражается следующей формулой:

Здесь значения параметров a и b определяют соответственно точную высоту и крутизну прямой. Параметр a называется пересечением с вертикальной осью или константой, а b — градиентом, наклоном линии или угловым коэффициентом. Например, в соотнесенности между температурными шкалами по Цельсию и по Фаренгейту a = 32 и b = 1.8. Подставив в наше уравнение значения a и b, получим:

Для вычисления 10°С по Фаренгейту мы вместо x подставляем 10:

Таким образом, наше уравнение сообщает, что 10°С равно 50°F, и это действительно так. Используя Python и возможности визуализации pandas, мы можем легко написать функцию, которая переводит градусы из Цельсия в градусы Фаренгейта и выводит результат на график:

Этот пример сгенерирует следующий ниже линейный график:

Обратите внимание, как синяя линия пересекает 0 на шкале Цельсия при величине 32 на шкале Фаренгейта. Пересечение a — это значение y, при котором значение x равно 0.

Наклон линии с неким угловым коэффициентом определяется параметром b; в этом уравнении его значение близко к 2. Как видно, диапазон шкалы Фаренгейта почти вдвое шире диапазона шкалы Цельсия. Другими словами, прямая устремляется вверх по вертикали почти вдвое быстрее, чем по горизонтали.

Остатки

К сожалению, немногие связи столь же чистые, как перевод между градусами Цельсия и Фаренгейта. Прямолинейное уравнение редко позволяет нам определять y строго в терминах x. Как правило, будет иметься ошибка, и, таким образом, уравнение примет следующий вид:

Здесь, ε — это ошибка или остаточный член, обозначающий расхождение между значением, вычисленным параметрами a и b для данного значения x и фактическим значением y. Если предсказанное значение y — это ŷ, то ошибка — это разность между обоими:

Такая ошибка называется остатком. Остаток может возникать из-за случайных факторов, таких как погрешность измерения, либо неслучайных факторов, которые неизвестны. Например, если мы пытаемся предсказать вес как функцию роста, то неизвестные факторы могут состоять из диеты, уровня физической подготовки и типа телосложения (либо просто эффекта округления до самого близкого килограмма).

Если для a и b мы выберем неидеальные параметры, то остаток для каждого x будет больше, чем нужно. Из этого следует, что параметры, которые мы бы хотели найти, должны минимизировать остатки во всех значениях x и y.

Обычные наименьшие квадраты

Для того, чтобы оптимизировать параметры линейной модели, мы бы хотели создать функцию стоимости, так называемую функцией потери, которая количественно выражает то, насколько близко наши предсказания укладывается в данные. Мы не можем просто взять и просуммировать положительные и отрицательные остатки, потому что даже самые большие остатки обнулят друг друга, если их знаки противоположны.

Прежде, чем вычислить сумму, мы можем возвести значения в квадрат, чтобы положительные и отрицательные остатки учитывались в стоимости. Возведение в квадрат также создает эффект наложения большего штрафа на большие ошибки, чем на меньшие ошибки, но не настолько много, чтобы самый большой остаток всегда доминировал.

Выражаясь в терминах задачи оптимизации, мы стремимся выявить коэффициенты, которые минимизируют сумму квадратов остатков. Этот метод называется обычными наименьшими квадратами, от англ. Ordinary Least Squares (OLS), и формула для вычисления наклона линии регрессии по указанному методу выглядит так:

Хотя она выглядит сложнее предыдущих уравнений, на самом деле, эта формула представляет собой всего лишь сумму квадратов остатков, деленную на сумму квадратов отклонений от среднего значения. В данном уравнении используется несколько членов из других уравнений, которые уже рассматривались, и мы можем его упростить, приведя к следующему виду:

Пересечение (a) — это член, позволяющий прямой с заданным наклоном проходить через среднее значение X и Y:

Значения a и b — это коэффициенты, получаемые в результате оценки методом обычных наименьших квадратов.

Наклон и пересечение

Мы уже рассматривали функции covariance , variance и mean , которые нужны для вычисления наклона прямой и точки пересечения для данных роста и веса пловцов. Поэтому вычисление наклона и пересечения имеют тривиальный вид:

В результате будет получен наклон приблизительно 0.0143 и пересечение приблизительно 1.6910.

Интерпретация

Величина пересечения — это значение зависимой переменной (логарифмический вес), когда независимая переменная (рост) равна нулю. Для получения этого значения в килограммах мы можем воспользоваться функцией np.exp , обратной для функции np.log . Наша модель дает основания предполагать, что вероятнее всего вес олимпийского пловца с нулевым ростом будет 5.42 кг. Разумеется, такое предположение лишено всякого смысла, к тому же экстраполяция за пределы границ тренировочных данных является не самым разумным решением.

Величина наклона показывает, насколько y изменяется для каждой единицы изменения в x. Модель исходит из того, что каждый дополнительный сантиметр роста прибавляет в среднем 1.014 кг. веса олимпийских пловцов. Поскольку наша модель основывается на данных о всех олимпийских пловцах, она представляет собой усредненный эффект от увеличения в росте на единицу без учета любого другого фактора, такого как возраст, пол или тип телосложения.

Визуализация

Результат линейного уравнения можно визуализировать при помощи имплементированной ранее функции regression_line и простой функции от x, которая вычисляет ŷ на основе коэффициентов a и b.

Функция regression_line возвращает функцию от x, которая вычисляет a + bx.

Указанная функция может также использоваться для вычисления каждого остатка, показывая степень, с которой наша оценка ŷ отклоняется от каждого измеренного значения y.

График остатков — это график, который показывает остатки на оси Y и независимую переменную на оси X. Если точки на графике остатков разбросаны произвольно по обе стороны от горизонтальной оси, то линейная модель хорошо подогнана к нашим данным:

За исключением нескольких выбросов на левой стороне графика, график остатков, по-видимому, показывает, что линейная модель хорошо подогнана к данным. Построение графика остатков имеет важное значение для получения подтверждения, что линейная модель применима. В линейной модели используются некоторые допущения относительно данных, которые при их нарушении делают не валидными модели, которые вы строите.

Допущения

Первостепенное допущение линейной регрессии состоит в том, что, безусловно, существует линейная зависимость между зависимой и независимой переменной. Кроме того, остатки не должны коррелировать друг с другом либо с независимой переменной. Другими словами, мы ожидаем, что ошибки будут иметь нулевое среднее и постоянную дисперсию по отношению к зависимой и независимой переменной. График остатков позволяет быстро устанавливать, является ли это действительно так.

Левая сторона нашего графика имеет более крупные значения остатков, чем правая сторона. Это соответствует большей дисперсии веса среди более низкорослых спортсменов. Когда дисперсия одной переменной изменяется относительно другой, говорят, что переменные гетероскедастичны, т.е. их дисперсия неоднородна. Этот факт представляет в регрессионном анализе проблему, потому что делает не валидным допущение в том, что модельные ошибки не коррелируют и нормально распределены, и что их дисперсии не варьируются вместе с моделируемыми эффектами.

Гетероскедастичность остатков здесь довольно мала и особо не должна повлиять на качество нашей модели. Если дисперсия на левой стороне графика была бы более выраженной, то она привела бы к неправильной оценке дисперсии методом наименьших квадратов, что в свою очередь повлияло бы на выводы, которые мы делаем, основываясь на стандартной ошибке.

Качество подгонки и R-квадрат

Хотя из графика остатков видно, что линейная модель хорошо вписывается в данные, т.е. хорошо к ним подогнана, было бы желательно количественно измерить качество этой подгонки. Коэффициент детерминации R 2 , или R-квадрат, варьируется в интервале между 0 и 1 и обозначает объяснительную мощность линейной регрессионной модели. Он вычисляет объясненную долю изменчивости в зависимой переменной.

Обычно, чем ближе R 2 к 1, тем лучше линия регрессии подогнана к точкам данных и больше изменчивости в Y объясняется независимой переменной X. R 2 можно вычислить с помощью следующей ниже формулы:

Здесь var(ε) — это дисперсия остатков и var(Y) — дисперсия в Y. В целях понимания смысла этой формулы допустим, что вы пытаетесь угадать чей-то вес. Если вам больше ничего неизвестно об испытуемых, то наилучшей стратегией будет угадывать среднее значение весовых данных внутри популяции в целом. Таким путем средневзвешенная квадратичная ошибка вашей догадки в сравнении с истинным весом будет var(Y), т.е. дисперсией данных веса в популяции.

Но если бы я сообщил вам их рост, то в соответствии с регрессионной моделью вы бы предположили, что a + bx. В этом случае вашей средневзвешенной квадратичной ошибкой было бы или дисперсия остатков модели.

Компонент формулы var(ε)/var(Y) — это соотношение средневзвешенной квадратичной ошибки с объяснительной переменной и без нее, т. е. доля изменчивости, оставленная моделью без объяснения. Дополнение R 2 до единицы — это доля изменчивости, объясненная моделью.

Как и в случае с r , низкий R 2 не означает, что две переменные не коррелированы. Просто может оказаться, что их связь не является линейной.

Значение R 2 описывает качество подгонки линии регрессии к данным. Оптимально подогнанная линия — это линия, которая минимизирует значение R 2 . По мере удаления либо приближения от своих оптимальных значений R 2 всегда будет расти.

Левый график показывает дисперсию модели, которая всегда угадывает среднее значение для , правый же показывает меньшие по размеру квадраты, связанные с остатками, которые остались необъясненными моделью f. С чисто геометрической точки зрения можно увидеть, как модель объяснила большинство дисперсии в y. Приведенный ниже пример вычисляет R 2 путем деления дисперсии остатков на дисперсию значений y:

В результате получим значение 0.753. Другими словами, более 75% дисперсии веса пловцов, выступавших на Олимпийских играх 2012 г., можно объяснить ростом.

В случае простой регрессионной модели (с одной независимой переменной), связь между коэффициентом детерминации R 2 и коэффициентом корреляции r является прямолинейной:

Коэффициент корреляции r может означать, что половина изменчивости в переменной Y объясняется переменной X, но фактически R 2 составит 0.5 2 , т.е. 0.25.

Множественная линейная регрессия

Пока что в этой серии постов мы видели, как строится линия регрессии с одной независимой переменной. Однако, нередко желательно построить модель с несколькими независимыми переменными. Такая модель называется множественной линейной регрессией.

Каждой независимой переменной потребуется свой собственный коэффициент. Вместо того, чтобы для каждой из них пытаться подобрать букву в алфавите, зададим новую переменную β (бета), которая будет содержать все наши коэффициенты:

Такая модель эквивалентна двухфакторной линейно-регрессионной модели, где β₁ = a и β₂ = b при условии, что x₁ всегда гарантированно равен 1, вследствие чего β₁ — это всегда константная составляющая, которая представляет наше пересечение, при этом x₁ называется (постоянным) смещением уравнения регрессии, или членом смещения.

Обобщив линейное уравнение в терминах β, его легко расширить на столько коэффициентов, насколько нам нужно:

Каждое значение от x₁ до x_n соответствует независимой переменной, которая могла бы объяснить значение y. Каждое значение от β₁ до β_n соответствует коэффициенту, который устанавливает относительный вклад независимой переменной.

Простая линейная регрессия преследовала цель объяснить вес исключительно с точки зрения роста, однако объяснить вес людей помогает много других факторов: их возраст, пол, питание, тип телосложения. Мы располагаем сведениями о возрасте олимпийских пловцов, поэтому мы смогли бы построить модель, которая учитывает и эти дополнительные данные.

До настоящего момента мы предоставляли независимую переменную в виде одной последовательности значений, однако при наличии двух и более параметров нам нужно предоставлять несколько значений для каждого x. Мы можем воспользоваться функциональностью библиотеки pandas, чтобы выбрать два и более столбцов и управлять каждым как списком, но есть способ получше: матрицы.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Темой следующего поста, поста №3, будут матричные операции, нормальное уравнение и коллинеарность.

Линейная регрессия на Python: объясняем на пальцах

Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!

Что такое регрессия?

Регрессия ищет отношения между переменными.

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.

Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.

Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.

Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.

Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.

Зависимые данные называются зависимыми переменными, выходами или ответами.

Независимые данные называются независимыми переменными, входами или предсказателями.

Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.

Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.

Когда вам нужна регрессия?

Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.

Где она вообще нужна?

Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.

Линейная регрессия

Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.

Постановка проблемы

Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.

Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.

Простая линейная регрессия

Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.

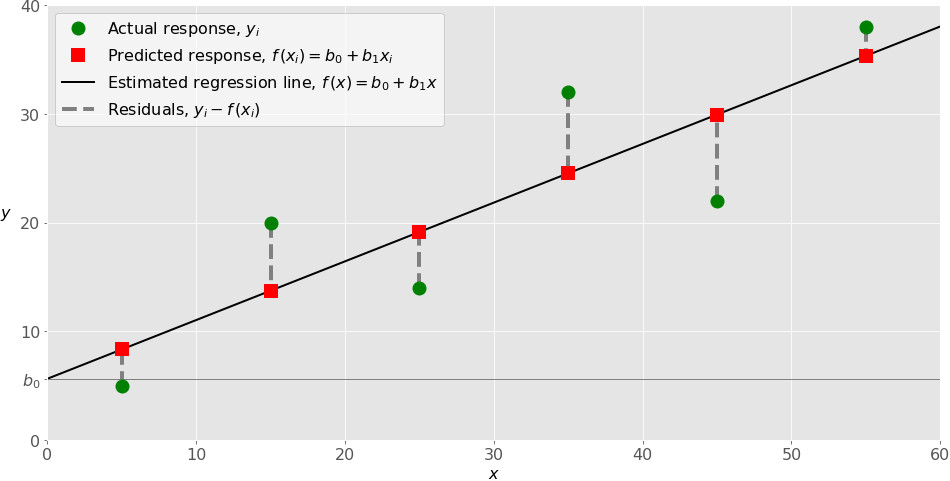
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.

Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.

Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).

Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.

Реализуйте линейную регрессию в Python

Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.

Пакеты Python для линейной регрессии

NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.

Незнакомы с NumPy? Начните с официального гайда.

Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.

Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.

Простая линейная регрессия со scikit-learn

Начнём с простейшего случая линейной регрессии.

Следуйте пяти шагам реализации линейной регрессии:

1. Импортируйте необходимые пакеты и классы.
2. Предоставьте данные для работы и преобразования.
3. Создайте модель регрессии и приспособьте к существующим данным.
4. Проверьте результаты совмещения и удовлетворительность модели.
5. Примените модель для прогнозов.

Это общие шаги для большинства подходов и реализаций регрессии.

Шаг 1: Импортируйте пакеты и классы

Первым шагом импортируем пакет NumPy и класс LinearRegression из sklearn.linear_model :

Теперь у вас есть весь функционал для реализации линейной регрессии.

Фундаментальный тип данных NumPy – это тип массива numpy.ndarray . Далее под массивом подразумеваются все экземпляры типа numpy.ndarray .

Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.

Шаг 2 : Предоставьте данные

Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.ndarray ) или похожими объектами. Вот простейший способ предоставления данных регрессии:

Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape() на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).

Вот как x и y выглядят теперь:

Шаг 3: Создайте модель

На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.

Давайте сделаем экземпляр класса LinearRegression , который представит модель регрессии:

Эта операция создаёт переменную model в качестве экземпляра LinearRegression . Вы можете предоставить несколько опциональных параметров классу LinearRegression :

• fit_intercept – логический ( True по умолчанию) параметр, который решает, вычислять отрезок b₀ ( True ) или рассматривать его как равный нулю ( False ).
• normalize – логический ( False по умолчанию) параметр, который решает, нормализовать входные переменные ( True ) или нет ( False ).
• copy_X – логический ( True по умолчанию) параметр, который решает, копировать ( True ) или перезаписывать входные переменные ( False ).
• n_jobs – целое или None (по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях. None означает отсутствие процессов, при -1 используются все доступные процессоры.

Наш пример использует состояния параметров по умолчанию.

Пришло время задействовать model . Сначала вызовите .fit() на model :

С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self — переменную model . Поэтому можно заменить две последние операции на:

Эта операция короче и делает то же, что и две предыдущие.

Шаг 4: Получите результаты

После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.

Вы можете получить определения (R²) с помощью .score() , вызванной на model :

.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².

model содержит атрибуты .intercept_ , который представляет собой коэффициент, и b₀ с .coef_ , которые представляют b₁:

Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.

Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.

Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:

Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.

Шаг 5: Предскажите ответ

Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.

Получите предсказанный ответ, используя .predict() :

Применяя .predict() , вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.

Вот почти идентичный способ предсказать ответ:

В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.

Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.

Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1) , x.flatten() или x.ravel() при умножении с помощью model.coef_ .

На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:

Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new . Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.

О LinearRegression вы узнаете больше из официальной документации.

Теперь у вас есть своя модель линейной регрессии!