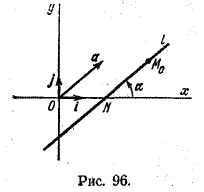
Пусть на плоскости, где имеется прямоугольная декартова система координат, прямая l проходит через точку М0 параллельно направляющему вектору а (рис. 96).
Если прямая l пересекает ось Ох (в точке N), то под углом прямой l с осью Ох будем понимать угол α, на который необходимо повернуть ось Ох вокруг точки N в направлении, обратном вращению часовой стрелки, чтобы ось Ох совпала с прямой l. (Имеется в виду угол, меньший 180°.)
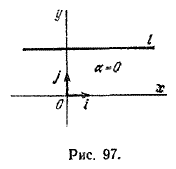
Этот угол называют углом наклона прямой. Если прямая l параллельна оси Ох, то угол наклона принимается равным нулю (рис. 97).
Тангенс угла наклона прямой называется угловым коэффициентом прямой и обычно обозначается буквой k:
Если α = 0, то и k = 0; это означает, что прямая параллельна оси Ох и ее угловой коэффициент равен нулю.
Если α = 90°, то k = tg α не имеет смысла: это означает, что прямая, перпендикулярная оси Ох (т. е. параллельная оси Оу), не имеет углового коэффициента.
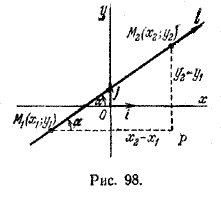
Угловой коэффициент прямой можно вычислить, если известны координаты двух каких-либо точек этой прямой. Пусть даны две точки прямой: M1(x1; у1) и M2(x2; у2) и пусть, например, 0 x1, у2 > у1 (рис. 98).
Тогда из прямоугольного треугольника M1РM2 находим
Аналогично доказывается, что формула (2) верна и в случае 90° 3 х + 3у — 7 = 0.
Приведем данное уравнение к виду
Следовательно, k = tg α = — 1 /√ 3 , откуда α = 150°
Задача 5. Составить уравнение прямой, проходящей через точку Р(3; -4), с угловым коэффициентом k = 2 /5
Задача 6. Составить уравнение прямой, проходящей через точку Q (-3; 4) и составляющей с положительным направлением оси Ох угол 30°.
Если α = 30°, то k = tg 30° = √ 3 /3. Подставив в уравнение (4) значения x1, y1 и k, получим
- Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»
- Найдите уравнение кривой, проходящей через точку М ( — 1 ; 3), если угловой коэффициент касательной в любой точке кривой равен утроенному квадрату абсциссы точки касания?
- Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 2lnx в его точке с абсциссой х = 2?
- Найдите угловой коэффициент касательной , проведенной к графику функции y = 3x — 2cosx в точке с абсциссой Xo = 0?
- Найдите угол наклона к оси абсцисс касательной, проведённой к кривой f(x) = (x — 3)(x — 2) в точке пересечения этой кривой с осью ординат?
- Найти уравнение кривой, проходящей через точку А(5 ; — 1), если угловой коэффициент касательной в любой её точке равен 4х — 8?
- Путь, пройденный материальной точкой S = 3t² — 2t + 4?
- Составьте уравнение кривой, проходящей через точку ( — 2 ; 8), если угловой коэффициент касательной в любой тчке касания равен 2x — 4?
- К кривой y = 1 / 2x — x ^ 1 / 2 в некоторой точке проведена касательная с угловым коэффициентом 0?
- Найдите угловой коэффициент касательной к графику функции y = 3x — 2cos x в точке с абсциссой x0 = 0?
- Записать уравнение касательной к кривой y = x ^ 2 — 7x + 3 в точке с абсциссой x = 1?
- Найдите угловой коэффициент касательной, проведенной к кривой у = 6 / х в точке х = 3 ?
- 💡 Видео
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»
Разделы: Математика
I. Обыкновенные дифференциальные уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Решением дифференциального уравнения называется такая функция 
, которая обращает это уравнение в тождество.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение
1. Рассмотрим дифференциальное уравнение первого порядка
Решением этого уравнения является функция y = 5 ln x. Действительно, 
, подставляя y’ в уравнение, получим 
– тождество.
А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция 
– решение этого уравнения.
Действительно, 
.
Подставляя эти выражения в уравнение, получим: 
, 
– тождество.
А это и значит, что функция 
– есть решение этого дифференциального уравнения.
Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.
Общим решением дифференциального уравнения называется функция вида 
,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.
Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
1.Найти частное решение дифференциального уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения, получим 
Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде 
.
— общее решение дифференциального уравнения.
Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3 2 + 4 2 = C 2 ; C=5.
Подставляя С=5 в общее решение, получим x 2 +y 2 = 5 2 .
Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.
2. Найти общее решение дифференциального уравнения 
Решением этого уравнения является всякая функция вида 
, где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: 
, 
.
Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения 
.
Например, непосредственной подстановкой можно убедиться, что функции 
являются решениями уравнения 
.
Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши.
Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x0) = y0, называется решением задачи Коши.
Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y) при условии y(x0) = y0,, означает найти интегральную кривую уравнения y’ = f(x,y) которая проходит через заданную точку M0(x0,y0).
II. Дифференциальные уравнения первого порядка
2.1. Основные понятия
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.
В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.
Общим решением дифференциального уравнения первого порядка называется функция вида 
, которая содержит одну произвольную постоянную.
Пример. Рассмотрим дифференциальное уравнение первого порядка 
.
Решением этого уравнения является функция 
.
Действительно, заменив в данном уравнении, 
его значением, получим
то есть 3x=3x
Следовательно, функция является общим решением уравнения при любом постоянном С.
Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения , получим 
откуда C = 0.
Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 
– частное решение.
2.2. Дифференциальные уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы 
, где f(x) и g(y)– заданные функции.
Для тех y, для которых 
, уравнение y’=f(x)g(y) равносильно уравнению, 
в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».
Уравнение вида называется уравнением с разделёнными переменными.
Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций 
и f(x), C произвольная постоянная.
Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными
- Производную функции переписать через её дифференциалы
- Разделить переменные.
- Проинтегрировать обе части равенства, найти общее решение.
- Если заданы начальные условия, найти частное решение.
Решить уравнение y’ = xy
Решение. Производную функции y’ заменим на 
разделим переменные 
проинтегрируем обе части равенства:
Ответ: 
Найти частное решение уравнения
Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде 
Отсюда 
Интегрируя обе части последнего равенства, найдем 
Подставив начальные значения x0 = 1, y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл будет 
или 
Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом 
Решение. Согласно условию 
Это уравнение с разделяющимися переменными. Разделив переменные, получим: 
Проинтегрировав обе части уравнения, получим: 
Используя начальные условия, x = 2 и y = — 3 найдем C:
Следовательно, искомое уравнение имеет вид 
2.3. Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)
где f(x) и g(x) — некоторые заданные функции.
Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y
Если 
то уравнение y’ = f(x)y + g(x) называется неоднородным.
Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: 
где С – произвольная постоянная.
В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: 
.
Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой 
,
т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения 
данного уравнения.
Для линейного неоднородного уравнения вида 
y’ = kx + b,
где k и b— некоторые числа и 
частным решением будет являться постоянная функция 
. Поэтому общее решение имеет вид 
.
Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой .
Следовательно, 
где С – произвольная постоянная.
Ответ: 
2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли
Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.
Алгоритм решения линейного дифференциального уравнения первого порядка
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ = u’v + uv’
3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы u вынести за скобки: 
5. Из скобки, приравняв ее к нулю, найти функцию 
Это уравнение с разделяющимися переменными: 
Разделим переменные и получим: 
Откуда 
. 
.
6. Подставить полученное значение v в уравнение 
(из п.4):
и найти функцию 
Это уравнение с разделяющимися переменными: 
7. Записать общее решение в виде: 
, т.е. 
.
Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0
Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’ в данное уравнение, получим 
Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки
Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: 
Найдем функцию v: 
Подставим полученное значение v в уравнение 
Получим: 
Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: 
Найдем функцию u = u(x,c) 
Найдем общее решение: 
Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0: 
Ответ: 
III. Дифференциальные уравнения высших порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0
Общим решением дифференциального уравнения второго порядка называется функция вида 
, в которую входят две произвольные постоянные C1 и C2.
Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего при некоторых значениях произвольных постоянных C1 и C2.
3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.
Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.
2. Составить его характеристическое уравнение, обозначив y» через r 2 , y’ через r, yчерез 1: r 2 + pr +q = 0
3.Вычислить дискриминант D = p 2 -4q и найти корни характеристического уравнения; при этом если:
а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня 
. Общее решение дифференциального уравнения выражается в виде 
, где C1 и C2 — произвольные постоянные.
б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни 
. Общее решение дифференциального уравнения выражается в виде 
Общее решение 
Дифференцируя общее решение, получим 
Составим систему из двух уравнений 
Подставим вместо 
,
и 
заданные начальные условия:
Таким образом, искомым частным решением является функция
.
2. Найти частное решение уравнения
