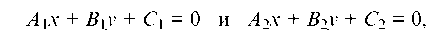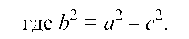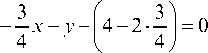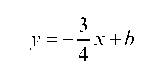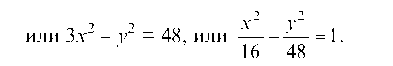Найти уравнение каждой из 2 прямых совокупность которых дана уравнением (3 видео)

1.3. Аналитическая геометрия. Аналитическая геометрия на плоскости

1.3.1. Аналитическая геометрия на плоскости

Если на плоскости произвольно взята декартова система координат, то всякое уравнение первой степени относительно текущих координат х и у

где А и B одновременно не равны нулю, определяет прямую в этой системе координат.

Верно и обратное утверждение: в декартовой системе координат всякая прямая может быть представлена уравнением первой степени вида (1.24).

Уравнение (1.24) называется общим уравнением прямой.

Углом наклона прямой к оси Ох называется наименьший угол j, на который нужно повернуть в положительном направлении ось абсцисс до ее совпадения с данной прямой. Направление любой прямой характеризуется ее угловым коэффициентом к, который определяется как тангенс угла наклона j этой прямой к оси Ох, т. е.

Исключение составляет только лишь прямая, перпендикулярная оси Ох, которая не имеет углового коэффициента.

Уравнение прямой, имеющей угловой коэффициент к и пересекающей ось Оу в точке, ордината которой равна b (начальная ордината), записывается в виде:

Частные случаи уравнения (1.24) приведены в следующей таблице.

Угловой коэффициент к прямой, заданной общим уравнением Ax + By + C= 0, находится как коэффициент при х в выражении у через х:

Угловой коэффициент к прямой, заданной двумя точками вычисляется по формуле

Уравнением прямой в отрезках называется уравнение вида:

где а и b — соответственно абсцисса и ордината точек пересечения прямой с осями Ох и Oy, т. е. длины отрезков, отсекаемых прямой на координатных осях, взятые с определенными знаками.

Уравнение прямой, проходящей через точкуИ имею

щей угловой коэффициент к, записывается в виде:

Пучком прямых называется совокупность прямых плоскости, проходящих через одну и ту же точку А — центр пучка. Уравнение (1.28) можно рассматривать как уравнение пучка прямых, поскольку любая прямая пучка может быть получены из уравнения (1) при соответствующем значении углового коэффициента к. Исключение составляет лишь одна прямая пучка, которая параллельна оси Oy — ее уравнение х = xA.

Уравнение прямой, проходящей через две данные точки имеет вид:

Если точки A и B определяют прямую, параллельную оси Или оси, то уравнение такой прямой за

писывается соответственно в виде:

Условия пересечения, параллельности или совпадения двух прямых, заданными своими общими уравнениями

приведены в следующей таблице.

Если известны угловые коэффициенты прямых, то ус

ловие параллельности этих прямых состоит в равенстве их угловых коэффициентов:

Условие перпендикулярности двух прямых, угловые коэффициенты которых соответственно равныСостоит в выполнении соотношения

т. е. угловые коэффициенты этих прямых обратны по абсолютной величине и противоположны по знаку.

Под углом между двумя прямыми понимается один из двух смежных углов, образованных при их пересечении. Тангенс угла j между двумя прямыми, угловые коэффициенты которых соответственно равны к1 и к2, вычисляется по формуле

причем знак «плюс» соответствует острому углу, а знак «минус» — тупому.

Уравнение окружности с центром в точке S^; b) и радиусом r имеем вид:

Это каноническое уравнение окружности (рис. 7).

Уравнение второй степени относительно текущих координат х и у является уравнением окружности тогда и только тогда, когда в этом уравнении коэффициенты при квадратах координат равны, а член с произведением координат отсутствует. Таким образом, это уравнение имеет вид:

В этом случае говорят, что окружность задана общим уравнением.

Для определения координат центра и радиуса окружности, заданной общим уравнением, надо с помощью тождественных преобразований уравнение (1.35) привести к виду (1.34).

Эллипс есть геометрическое место точек, сумма расстояний которых от двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная (2а), большая, чем расстояние между фокусами (2с).

Простейшее уравнение эллипса получается, если расположить координатную систему следующим образом: за ось Оx принять прямую, проходящую через фокусы F1 и F2, а за ось Оу — перпен-

дикуляр к оси абсцисс в середине отрезка F1F2 (рис. 8). Тогда уравнение эллипса примет вид:

Точки А1 и А2, B1 и B2 пересечения эллипса с его осями симметрии (координатными осями) называются вершинами эллипса. Отрезки А1А2 = 2а и B1B2 = 2b называются осями эллипса, причем А1А2 — большой осью, а B1B2 — малой осью, так как а > b. Таким образом, параметры а и b, входящие в уравнение эллипса, равны его полуосям.

Эксцентриситетом эллипса называется отношение расстояния между фокусами к его большой оси, т. е.

Очевидно, что е а и уже большой осью будет отрезок B1B2 = 2b, а малой осью — отрезок А1А2 = 2а. Эксцентриситет такого эллипса вычисляется по формуле

Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная (2а), меньшая, чем расстояние между фокусами (2с).

Простейшее уравнение гиперболы получается, если расположить координатную систему следующим образом: за ось Ох принять прямую, проходящую через фокусыА за ось Оу — перпендикуляр в середине отрезка(рис. 10). Тогда уравнение гиперболы примет вид:

Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках А1 и А2, называемых вершинами гиперболы. Отрезок.Называется действительной осью гиперболы, а отрезок— мнимой осью гиперболы.

Таким образом, параметры а и b, входящие в уравнение гиперболы, равны ее полуосям.

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к ее действительной оси:

Ее асимптоты те же, что и у гиперболы (1.39).

Гиперболы (1.39) и (1.42) называются сопряженными. Гипербола называется равносторонней, если ее действительные и мнимые оси равны, т. е. а = b. Простейшее уравнение равносторонней гиперболы имеет вид:

Если мнимая ось гиперболы направлена по оси Ох и имеет длину 2а, а действительная ось длиной 2b направлена по оси Oy, то уравнение гиперболы (рис. 11) имеет вид:

Эксцентриситет такой гиперболы вычисляется по формуле

Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой параболы.

Величина р, равная расстоянию от фокуса до директрисы, называется параметром параболы; прямая, проходящая через фокус параболы перпендикулярно ее директрисе, называется осью, а точка пересечения параболы с ее осью — вершиной параболы.

Простейшее уравнение параболы получается, если координатная система расположена следующим образом: за одну из координатных осей берется ось параболы, а за другую — прямая, перпендикулярная оси параболы и проведенная посредине между фокусом и директрисой.

Тогда уравнение параболы примет вид:

определяет параболу, ось которой перпендикулярна оси абсцисс.

определяет параболу, ось которой перпендикулярна оси ординат.

Уравнения (1.48) и (1.49) приводятся к простейшему виду (1.44 — 1.47) путем тождественных преобразований с последующим параллельным переносом координатной системы.

Пример 1.16. Даны вершины А (2; 1), В (6; 3), C (4; 5) треугольника. Найти: 1) длину стороны АВ; 2) внутренний угол А в радианах с точностью до 0,01; 3) уравнение высоты, проведенной через вершину С; 4) уравнение медианы, проведенной через вершину С;

5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж.

Делаем чертеж (рис. 16).

1. Длину стороны АВ находим как расстояние между двумя точками А и В.

2. Для определения внутреннего угла А найдем уравнение прямой AC:

отсюда 2х — у — 3 = 0 или у = 2х — 3 и угловой коэффициент прямой AC равен: kAC = 2; далее находим уравнение прямой АВ:

Находим угол А отсюда

3. Уравнение высоты, проведенной через вершину C, ищем в виде у — yC = kCD (x — xC) и так как CD А прямой АВ, то

4. Для определения уравнения медианы CM находим координаты точки M, которая делит прямую АВ пополам

Уравнение прямой CM ищем в виде:

а это означает, что уравнение медианы имеет вид х = 4, т. е. прямая CM L Ох.

5. Точку пересечения высот треугольника найдем как точку К пересечения высот CD и BK.

Находим уравнение высоты ВК:

Решаем систему уравнений, описывающих прямые CD и BK:

Тогдат. е. координаты точ

ки К будут:

6. Для нахождения длины высоты CD запишем нормальное уравнение прямой АВ:

7. Находим систему линейных неравенств, определяющих внутреннюю область треугольника.

Найдем уравнение прямой BC:

Итак:

Берем любую точку, лежащую внутри треугольника, например, (4; 3) и подставляем ее координаты в левую часть уравнений прямых:

следовательно, система неравенств имеет вид:

Пример 1.17. Составить уравнение прямой I, проходящей через точку А (2; -4) и отстоящей от начала координат на расстоянии, равном 2 единицам.

Решение. Пусть уравнение искомой прямой имеет вид:

Для определения углового коэффициента к этой прямой воспользуемся тем, что она отстоит от начала координат на расстоянии, равном 2 единицам. Найдем это расстояние непосредственно. Уравнение перпендикуляра, опущенного из начала координат на прямую, имеет вид илиРешив совместно уравнения этих двух прямых

С другой стороны, по условию OC = 2. Таким образом, получаем уравнение для нахождения углового коэффициента к искомой прямой I:

получим координаты точки C их пересечения:

Отсюда находим расстояние от начала координат до прямой I:

В заключение отметим, что отыскивая уравнение прямой I в виде у — yA = k(x — Xa), мы предполагали тем самым, что эта прямая не параллельна оси ординат. Но очевидно, что прямая х = 2 (параллельная оси Оу) также удовлетворяет условию задачи, так как она проходит через точку А (2; -4) и отстоит от начала координат на расстоянии, равном 2 единицам (рис. 17).

Пример 1.18. Составить уравнения прямых, параллельных прямой 3х + 4у — 1 = 0 (I) и отстоящих от нее на расстоянии равном 1.

Решение. Уравнение каждой из прямых будем искать в виде Так как искомая прямая параллельна прямой I, то ее

угловой коэффициентИ, следовательно, ее уравнение при

нимает вид:

Для отыскания параметра b воспользуемся тем, что расстояние от любой точки прямой I, например, от точки А (3; -2) до прямой (*) согласно условию равно 1. Но это расстояние может быть вычислено и непосредственно. Запишем для этого

уравнение прямой h, проведенной из точки А перпендикулярно прямой I:

Решив, далее, совместно уравнения прямых h и I найдем координаты точки В их пересечения:

Тогда искомое расстояние равно длине отрезка АВ:

Приравнивая это выражение единице, получим уравнение относительно b:

Решения этого уравнения таковы:. Подставляя полученные значения b в уравнение (*), запишем уравнения искомых прямых:

Пример 1.19. Составить уравнение линии, расстояние каждой точки которой от точки F (8; 0) вдвое больше, чем от прямой х — 2 = 0. Сделать чертеж.

Пусть М(х; у) — текущая точка линии. По условию задачи MF = 2MN.

Возводя в квадрат и раскрывая скобки, получим

Это есть каноническое уравнение гиперболы (рис. 18).

Пример 1.20. Составить уравнение линии, каждая точка которой равноудалена от точки F (0; — 4) и от прямой у + 2 = 0. Сделать чертеж.

Если M(x; у) есть текущая точка линии, то по условию задачи MF = MN или

Подставляя координаты точек

И возводя в квадрат, после преобразований

Содержание

Решебник.Ру / Кузнецов Л.А. Аналитическая геометрия. Задача 12
Канонические уравнения прямой
Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей
Уравнения двух плоскостей, задающих прямую линию в пространстве
Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости
Направляющий вектор прямой, по которой пересекаются две плоскости
Переход к параметрическим и каноническим уравнениям прямой в пространстве
🎦 Видео

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Решебник.Ру / Кузнецов Л.А. Аналитическая геометрия. Задача 12

Канонические уравнения прямой

Постановка задачи. Найти канонические уравнения прямой, заданной как линия пересечения двух плоскостей (общими уравнениями)

План решения. Канонические уравнения прямой с направляющим вектором , проходящей через данную точку , имеют вид

. (1)

Поэтому, чтобы написать канонические уравнения прямой, необходимо найти ее направляющий вектор и какую-нибудь точку на прямой.

1. Так как прямая принадлежит одновременно обеим плоскостям, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей, т.е. согласно определению векторного произведения, имеем

. (2)

2. Выбираем какую-нибудь точку на прямой. Поскольку направляющий вектор прямой не параллелен хотя бы одной из координатных плоскостей, то прямая пересекает эту координатную плоскость. Следовательно, в качестве точки на прямой может быть взята точка ее пересечения с этой координатной плоскостью.

3. Подставляем найденные координаты направляющего вектора и точки в канонические уравнения прямой (1).

Замечание. Если векторное произведение (2) равно нулю, то плоскости не пересекаются (параллельны) и записать канонические уравнения прямой не представляется возможным.

Задача 12. Написать канонические уравнения прямой.

Канонические уравнения прямой:

где – координаты какой-либо точки прямой, – ее направляющий вектор.

Найдем какую-либо точку прямой . Пусть , тогда

Следовательно, – координаты точки, принадлежащей прямой.

Канонические уравнения прямой:

:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей

В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.

Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.

По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнения двух плоскостей, задающих прямую линию в пространстве

Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.

Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:

n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R

Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.

Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .

Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.

Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .

Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .

Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.

Рассмотрим решение примера

Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x — 2 y + z — 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , — 1 , 0 ) и N 0 ( 0 , — 1 3 , 1 ) прямой линии пересечения плоскостей.

Решение

Начнем с точки М 0 _. Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( — 1 ) + 1 = 0 1 — 2 · ( — 1 ) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0 .

В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.

Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , — 1 3 , 1 ) . Получаем 2 · 0 + 3 · — 1 3 + 1 = 0 0 — 2 · — 1 3 + 1 — 3 = 0 ⇔ 0 = 0 — 1 1 3 = 0 .

Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.

Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.

Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.

Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.

Решение

Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 .

Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.

Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:

x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 ⇔ x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z

Введем произвольное действительное число λ и примем, что z = λ .

Тогда x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z ⇔ x + 0 y = — 7 — 3 λ 2 x + 3 y = — 2 — 3 λ .

Для решения полученной системы уравнений применим метод Крамера:

∆ = 1 0 2 3 = 1 · 3 — 0 · 1 = 2 ∆ x = — 7 — 3 λ 0 — — 3 λ 3 = — 7 — 3 λ · 3 — 0 · ( — 2 — 3 λ ) = 21 — 9 λ ⇒ x = ∆ x ∆ = — 7 — 3 λ ∆ y = 1 — 7 — 3 λ 2 — 2 — 3 λ = 1 · — 2 — 3 λ — — 7 — 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ

Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = — 7 — 3 λ y = 4 + λ z = λ , где λ ∈ R .

Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = — 7 — 3 · 0 y = 4 + 0 z = 0 ⇔ x = — 7 y = 4 z = 0 .

Это позволяет нам получить координаты искомой точки — 7 , 4 , 0 .

Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей — 7 + 3 · 0 + 7 = 0 2 · ( — 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .

Ответ: — 7 , 4 , 0

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Направляющий вектор прямой, по которой пересекаются две плоскости

Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.

Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.

Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .

Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .

a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2

Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ — это параметр, который может принимать любые действительные значения, отличные от нуля.

Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y — 3 z — 2 = 0 x — z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.

Решение

Плоскости x + 2 y — 3 z — 2 = 0 и x — z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , — 3 и n 2 → = 1 , 0 , — 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:

a → = n → 1 × n 2 → = i → j → k → 1 2 — 3 1 0 — 1 = i → · 2 · ( — 1 ) + j → · ( — 3 ) · 1 + k → · 1 · 0 — — k → · 2 · 1 — j → · 1 · ( — 1 ) — i → · ( — 3 ) · 0 = — 2 · i → — 2 j → — 2 k →

Запишем ответ в координатной форме a → = — 2 , — 2 , — 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».

Ответ: a → = — 2 , — 2 , — 2

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z — координаты направляющего вектора прямой, x 1 , y 1 , z 1 — координаты некоторой точки прямой, а λ — параметр, принимающий произвольные действительные значения.

От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.

Рассмотрим написанное выше на примере.

Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.

Решение

Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , — 1 плоскости 2 x + y — z — 1 = 0 и n 2 → = ( 1 , 3 , — 2 ) плоскости x + 3 y — 2 z = 0 :

a → = n 1 → × n 2 → = i → j → k → 2 1 — 1 1 3 — 2 = i → · 1 · ( — 2 ) + j → · ( — 1 ) · 1 + k → · 2 · 3 — — k → · 1 · 1 — j → · 2 · ( — 2 ) — i → · ( — 1 ) · 3 = i → + 3 · j → + 5 · k →

Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .

Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ 2 x + y — z = 1 x + 3 y — 2 z = 0 .

Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 — 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :

2 x + y — z = 1 x + 3 y — 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R

Применяем для решения полученной системы уравнений метод Крамера:

∆ = 2 1 1 3 = 2 · 3 — 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 — 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ — ( 1 + λ ) · 1 = — 1 + 3 λ ⇒ y = ∆ y ∆ = — 1 + 3 λ 5 = — 1 5 + 3 5 · λ

Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 y = — 1 5 + 3 5 z = λ

Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = — 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Ответ: x — 1 1 = y — 1 3 = z — 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Данная задача имеет еще один способ решения.

Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .

Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z

Применим данный способ к решению задачи.

Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.

Решение

Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ .

Это параметрические уравнения прямой в пространстве.

Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ ⇔ λ = x — 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x — 3 5 1 5 = y + 1 5 3 5 = z 1

Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.

Ответ: x — 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ