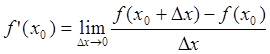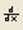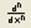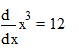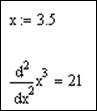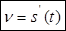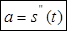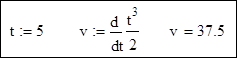Найти уравнение касательной в маткад

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

информатика

Студент группы СПД-13 Пестов В.В.

Код Подпись, дата Ф.И.О

Преподаватель Пинаев В.Н.

Для заданной функции :

1. Построить график функции и графики ее первой и второй производной в общих координатах.

2. Построить графики касательной и нормали к функции в точке ( x 0 = 3) 0 .

3. Найти точки локального экстремума функции f ( x ) и точки перегиба ( стационарные точки).

4. Определить значение функции в стационарных точках.

5. Определить первообразную + c и построить графики семейства первообразных.

1. Построить график функции и графики ее первой и второй производной в общих координатах.

Для построения графика функции и двух её производных в Mathcad нам необходимо получить уравнения производных первой и второй степенях. Это можно сделать и самому, не используя никаких программ:
f ‘( x )= x ‘* e — x + x *( e — x )’= e — x — x * e — x = e — x *(1- x )

f »(x)= (e -x )’*(1-x)+(e -x )*(1-x)’=- e -x *(1-x)- e -x = e -x (x-2)

Теперь, когда я вычисли обе производные, самое время построить их графики в Mathcad . Что у меня получилось, можно увидеть на рис.1:

Красной линией изображен график самой функции, зелёной и синей — графики первой и второй её производных соответственно.
Итак, первое задание выполнено.

2. Необходимо построить графики касательной и нормали к графику функции.

Для этого нам необходимо знать уравнения графиков касательной и нормали. Их я не знал, поэтому пришлось обратиться к всемогущему интернету. В нём я нашёл сайт, да хранит его могучий браузер Mozilla Firefox , который показал мне, глупому холопу, уравнения нужных мне функций. Поэтому, я счел нужным представить этот сайт, ибо без него я не смог бы выполнить эту работу ( http://www.fizmatik.ru/index.php?option=com_content&view=article&id=19&Itemid=20 ).

Уравнение касательной выглядит так:

y=f ‘(x 0 )*x+f(x 0 )-f ‘(x 0 )*x 0

Уравнение нормали имеет вид:

y=f(x 0 )-(x-x 0 ) / f ‘(x 0 )

Где х 0 =3 (точка, заданная по условию).

Теперь, когда у меня появились уравнения, осталось записать их в программе Mathcad . Вот какие графики у меня получились (рис.2):

Красная линия — график функции, синий — касательная к графику в точке х 0 , зелёный — нормаль к графику в точке х 0 .

Задание 2 можно считать выполненным.
3. Найти точки локального экстремума функции f ( x ) и точки перегиба ( стационарные точки).

Чтобы найти точки локального экстремума, необходимо приравнять первую производную функции к нулю.

f ‘( x )=0; e — x *(1- x )=0; 1- x =0;

x =1 — критическая точка, она же будет и стационарной (критическая точка — точка, где функция изменяет свое «направление»: если она возрастала, то начинает убывать (в моём случае) и наоборот). Стационарная точка — точка, в которой производная равна нулю.

С этим заданием я тоже справился.

4. Определить значение функции в стационарных точках.

Ну это совсем просто. Достаточно подставить точку х=1 в уравнение функции:

Я решил представить значение и в численном виде, оно будет равно:

Вот и это задание выполнено, осталось последнее.

5. Определить первообразную + c и построить графики семейства первообразных.

Для вычисления интеграла своей функции я вновь решил обратиться к всемогущему интернету. В великом браузере Mozilla Firefox мне был предоставлен во внимание сайт, который помог решить мою проблему, а именно, взять за меня интеграл от моей функции. И я не мог не представить его в своей работе ( http://matematikam.ru/calculate-online/indefinite-integral.php ).

Я позволил себе не менять язык, так как я не хотел нарушать всю прелестную форму данного сайта. И вот у меня теперь есть уравнение первообразной. Но мне то надо построить семейство первообразных. Я уже начал волноваться, ведь у меня всего одна формула, а мне надо построить несколько графиков, пока мне не подсказали, что нужно всего-то менять Constant . И вот я уже в Mathcad пишу формулы и, о чудо, у меня готовы графики семейства первообразных (рис.3):

Красной линией обозначен график первообразной, где const =0, а для других const =4;-4 соответственно.

Вот и выполнена моя курсовая работа. Пора подвести итоги.

В ходе выполнения этой работы, я познал такую замечательную программу, как Mathcad , приобрел небольшие навыки в обращении с ней, а также в очередной раз убедился в таком незыблемо величавом творении человека, как интернет, ибо перед ним мы должны падать на колени, ведь это наше детище, которое почти поработило нас. И я, презренный холоп, приклоняюсь перед ним. А также я благодарю своих наставников, Пинаева Владимира Николаевича и Шалаева Дмитрия Сергеевича, благодаря которым, такой холоп, как я, узнал и смог освоить программу Mathcad .

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Построение графиков в MathCad

В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Построение графика по точкам

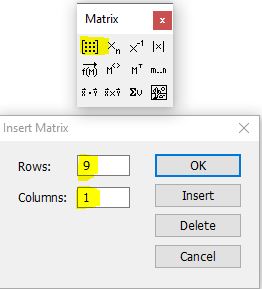
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)

Рис. 1. Создание матриц-столбцов

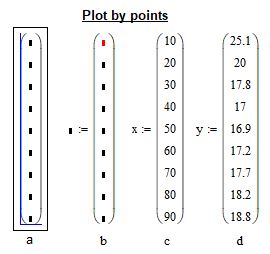
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.

Рис. 2. Заполнение матриц-столбцов для графика

На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)

Рис. 3. Создание заготовки для графика

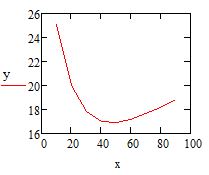
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)

Рис. 4. График по точкам

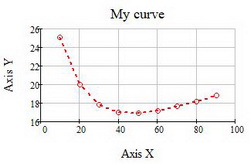
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)

Рис. 5. Настройка отображения графика

Видео:Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

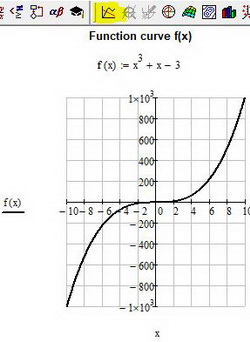
Построение графика функции f(x)

Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой

Рис. 6. Построение графика функции f(x)

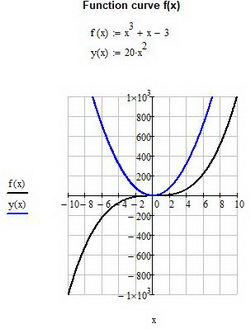
Чтобы построить два графика и более на одном поле (в тех же осях координат) сделайте следующее: введите вторую функцию, например y(x):=. , поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7

Рис. 7. Построение двух графиков функции

Видео:Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Построение эпюры в mathcad

Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:

— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании

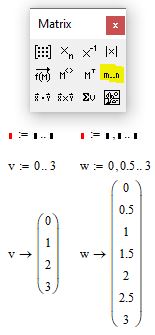
Ранжированная переменная по сути является матрицей-столбцом, разница лишь в том, что значение элементов в нее входящих представляют из себя определенную закономерность или последовательность чисел. Ранжированную переменную можно ввести воспользовавшись кнопкой Range Variable из панели Matrix. Первый маркер отвечает за начальное значение последовательности, второй — за конечное. По умолчаию шаг последовательности равен 1. Если после первого элемента ввести символ запятой и в появившемся маркере ввести следующее число вашей последовательности, то таким образом вы определите шаг, с которым будет заполняться ваша последовательность. Обратите внимание на пример ниже.

Рис. 8. Ввод ранжированной переменной

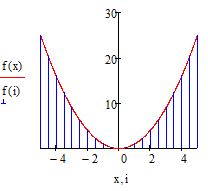
Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже

Рис. 9. Ввод ранжированной переменной

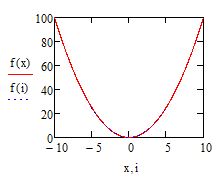
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже

Рис. 10. Построение эпюры. Шаг 1

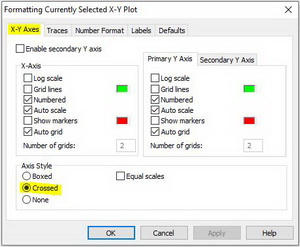
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.

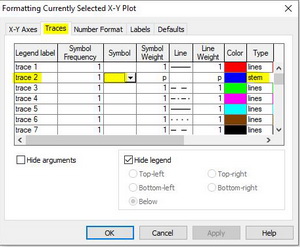
Рис. 11. Построение эпюры. Шаг 2

В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)

Рис. 12. Построение эпюры. Шаг 3

Видео:Mathcad-09. Пример: уравненияСкачать

Построение графика в полярных координатах в mathcad

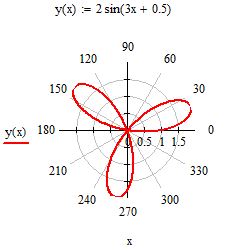
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)

Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph

Рис. 13. Создание загатовки для графика в полярных координатах

Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.

Рис. 14. Построение графика в полярной системе координат

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Видео:Уравнение касательнойСкачать

Дифференциальное исчисление в пакете MathCad. Определение и понятие производной. Встроенные функции решения краевых задач, заданных в форме Коши

Страницы работы

Фрагмент текста работы

Лабораторная работа № 6. Дифференциальное исчисление в пакете MathCad.

цель работы: освоение основных приемов вычисление производных высших порядков в пакете MathCad (4 часа)

1. Определение и понятие производной

2. Средства дифференцирования в MathCad

2.1 Примеры нахождения производных

3. Нахождение производной в общем виде

4. Физический смысл производной

4.1 Пример применения физического смысла производной

5. Геометрический смысл производной

5.1 Пример нахождения уравнения касательной функции в некоторой точке

6. Приложения производной

6.1. Экстремумы функции

6.2. Разложение функции в ряд Тейлора.

7. Встроенные функции решения краевых задач, заданных в форме Коши

7.2 Функция Odesolve()

7.2 Функция Rkfixed()

Порядок выполнения работы

Задание 1. Построение касательной к функции в точке

Задание 2. Физический смысл производной.

Задание 3. Определение экстремумов функции

Задание 4. Разложение функции в ряд Тейлора

Задание 5. Решение задачи Коши

Видео:Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

1. Определение и понятие производной

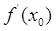
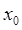
Производной функции в точке называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю т.е.

Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

2. Средства дифференцирования в MathCad

Оператор производной предназначен для нахождения значения производной функции в заданной точке.

Вызвать оператор производной можно следующими способами:

Используя ПИ производных и интегралов

для нахождения производной 1-го порядка

для нахождения производной n-го порядка

Для нахождения производной нужно:

1. 1. Определить точку (или диапазон), в которой будет найдена производная;

2. 2. Вызвать оператор нахождения производной:

v v появится шаблон нахождения производной 1-го порядка

v v шаблон нахождения производной n-го порядка

3. 3. Заполнить шаблон данными:

Видео:MathCAD. Given - FindСкачать

2.1 Примеры нахождения производных

1. Найти производную функции 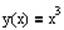в точке x=2.

2. Найти производную той же самой функции в точках x, на заданном интервале.

3.Найти вторую производную той же функции в точке x=3.5

Видео:Уравнение касательнойСкачать

3. Нахождение производной в общем виде

Для вывода на экран формулы нахождения производной необходимо:

v v на ПИ выбрать шаблон неопределенного интеграла производной;

v v заполнить его;

v v набрать на клавиатуре Ctrl+.(точка);

v v нажать ввод.

Видео:Числовое решение. Функция polyroots в MathCAD 14 (27/34)Скачать

4. Физический смысл производной

Пусть s=s(t) представляет закон прямолинейного движения материальной точки. Это уравнение выражает путь s, пройденный точкой, как функцию времени t. Обозначим через ∆s путь, пройденный за промежуток времени ∆tот момента t до t+∆t, то есть ∆s=s(t+∆t)-s(t).

Отношение 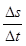называется средней скоростью точки за время от t до t+∆t.

Мгновенной скоростью точки в данный момент времени t называется предел средней скорости за промежуток от t до t+∆t, когда :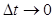

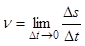
или

Ускорение точки в данный момент вычисляется по следующей формуле:

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

4.1 Пример применения физического смысла производной

Точка движется по закону 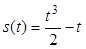. Определить ее мгновенную скорость в момент времени t=5 с.

Видео:Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

5. Геометрический смысл производной

Угловой коэффициент касательной к графику функции f(x) в точке a равен первой производной функции в данной точке: 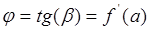, где

β — угол наклона касательной к оси Ох.

Уравнение касательной имеет вид:

— угловой коэффициент касательной к графику функции, в точке x=a

Видео:MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

5.1 Пример нахождения уравнения касательной функции в некоторой точке

Найти уравнение касательной к функции , в точке x₀ = 2 и ее наклон к оси Ох.

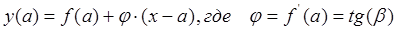
Видео:Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать

6. Приложения производной

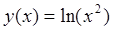
Видео:Вычисление простых выражений в MathCAD 14 (4/34) Часть 1Скачать

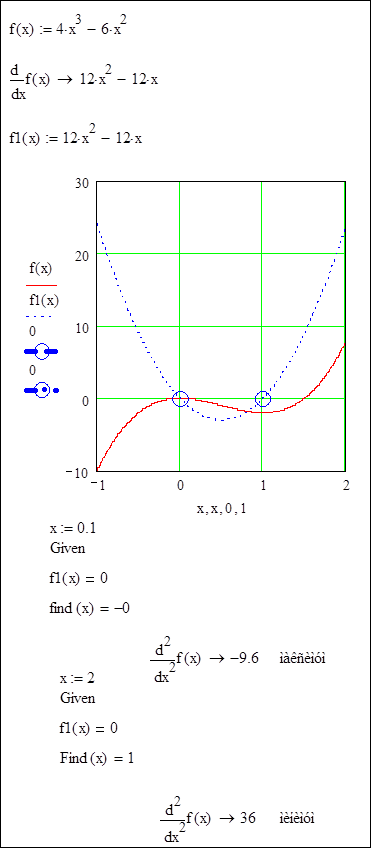
6.1. Экстремумы функции

Правило1 (признак нахождения экстремумов, основанный на исследовании знака первой производной):

Пусть 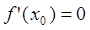, то если при переходе через точку x₀ функция f(x) меняет знак с + на – (с – на +), то x₀ – точка локального максимума (минимума).

Правило 2 (признак нахождения экстремумов, основанный на исследовании знака второй производной):

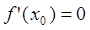
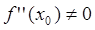
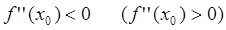
Пусть и , тогда если , то x₀ – точка локального максимума (минимума).

Пример нахождения экстремумов функции.

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

6.2. Разложение функции в ряд Тейлора.

Для приближенного определения значения функции f(x) разложим данную функцию в Ряд Тейлора в окрестности точки x=a.

🔍 Видео

14.1. Касательная к параметрически заданной функцииСкачать

3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать