Найти уравнение касательной главной нормали и бинормали

Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec$, $vec$, $vec$ называется репером Френе.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec$, $vec$, $vec$ не будет правой (по определению векторного произведения вектор $vectimesvec$ направлен так, что тройка векторов $vec$, $vec$, $vec=vectimesvec$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec$, $vec$, $vec<tilde>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac,,, z=frac, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_=2,, t_=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Видео:14.1. Касательная к параметрически заданной функцииСкачать

Касательная и нормаль к графику функции

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Основные формулы

Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной

Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓

Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Определения

Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.

Определение касательной приводится здесь. Уравнение касательной:
.

Касательная TM₀, нормаль M₀N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
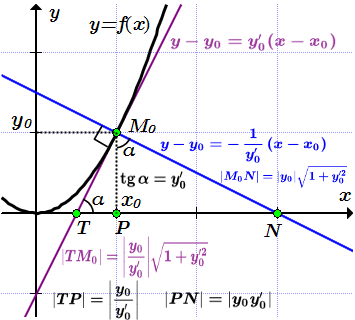
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Полезные формулы из аналитической геометрии

Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.

Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.

Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .

Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :

Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.

Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.

Уравнение прямой в отрезках, пересекающей оси координат в точках :
.

Видео:Геометрический смысл производной. Уравнение касательнойСкачать

Примеры решения задач

Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓

Пример 1

Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.

Находим значение функции при :
.

Находим производную:
.
Находим производную в точке :
;
.

Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .

Касательная и нормаль к графику функции y=x 2 в точке M₀(1;1).

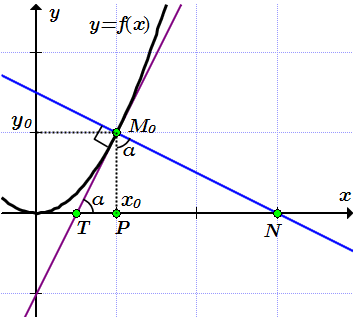
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.

Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .

Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.

Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка поднормали . Из прямоугольника имеем:
.

Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.

Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .

Пример 2

Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .

Находим значения переменных при .
;
.
Обозначим эту точку как .

Находим производные переменных x и y по параметру t .
;
;
;
;
.

Подставляя , находим производную y по x в точке .
.

Касательная и нормаль к циссоиде в точке (2;2).

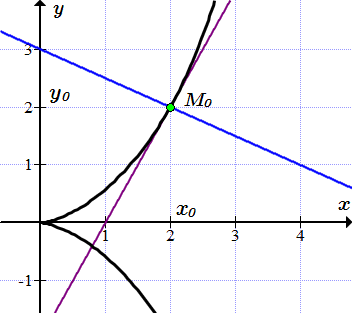
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.

Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.

Уравнение касательной: .
Уравнение нормали: .

Пример 3

Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .

Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.

Находим производную в заданной точке, подставляя .
;
.

Находим уравнение касательной по формуле (2).
;
;
;
.

Находим уравнение нормали по формуле (3).
;
;
;
.

Касательная и нормаль к циссоиде изображены на рисунке ⇑.

Уравнение касательной: .
Уравнение нормали: .

Пример 4

Найти угол между кривыми и .

Найдем множество точек пересечения кривых, решая систему уравнений.

Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .

Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.

Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.

Видео:Уравнение касательнойСкачать

Вывод формулы для угла между кривыми

Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .

Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .

Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.

В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .

На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .

При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.

1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).

2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:

.

Этот случай изображен на рисунке ⇑.

3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).

Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.

Автор: Олег Одинцов . Опубликовано: 30-06-2021

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Найти единичный вектор касательной главной нормали

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Касательная и нормаль к кривойСкачать

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Видео:Репетитор по математике ищет нормаль к плоскостиСкачать

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec =vec (t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec (t_0)neqvec $, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec (t_0)$.

Пусть $vec $ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec $).

Если $vec = $, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec $ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec -vec (t_0)$ и $vec (t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec (t_0)$, $vec (t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec $ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec -vec (t_0)$, $vec (t_0)$, $vec (t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec (t_0)timesvec (t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec $ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec (t_0) timesleft[vec (t_0),vec (t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec -vec (t_0)$, $vec (t_0)$, $vec (t_0)timesvec (t_0)$: begin left(vec -vec (t_0),, vec (t_0),, vec (t_0)timesvec (t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec =frac (t_0)> (t_0)|>. $$ Орт бинормали: $$ vec =frac (t_0)timesvec (t_0)> (t_0)timesvec (t_0)|>. $$ Орт главной нормали: $$ vec =frac (t_0) times[vec (t_0),,vec (t_0)]> (t_0) times [vec (t_0),,vec (t_0)]|>. $$

Правая тройка векторов $vec $, $vec $, $vec $ называется репером Френе.

Видео:5. Нормальное уравнение плоскости выводСкачать

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec $, $vec $, $vec $ не будет правой (по определению векторного произведения вектор $vec timesvec $ направлен так, что тройка векторов $vec $, $vec $, $vec =vec timesvec $

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec $, $vec $, $vec >$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac ,,, z=frac , $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec (t_0)$, $vec (t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec (t_0)$ и $vec (t_0)timesvec (t_0)$.

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_ =2,, t_ =-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Видео:Что такое нормаль?Скачать

Конспект лекций по высшей математике Введение в дифференциальную геометрию 2

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

КОНСПЕКТ ЛЕКЦИЙ ПО РАЗДЕЛУ КУРСА ВЫСШЕЙ МАТЕМАТИКИ

«ВВЕДЕНИЕ В ДИФФЕРЕНЦИАЛЬНУЮ ГЕОМЕТРИЮ»

для студентов направления подготовки 0709

«Геодезия, картография и землеустройство»

Составитель: доц. Абдулин Р.Н.

2.4 КРУГ КРИВИЗНЫ.

Рассмотрим кривую в натуральной параметризации:

Г:

в окрестности точки . Здесь и далее в скобках приводятся соответствующие формулы для произвольного параметра. Наряду с точкой М _о рассмотрим ещё две соседних точки М ₁ и М ₂ . Выше мы вводили понятие касательной, как предельное положение секущей М _о М ₁ при М ₁  М _о . Напомним, что вектор

(2.8)

‑ единичный вектор касательной, направленный в сторону возрастания параметра s .

О пределение 2.1 Кругом кривизны кривой Г в точке М _о называется предельное положение окружности, проходящей через точки М _о , М ₁ и М ₂ при М ₁  М _о и М ₂  М _о . Радиус этой окружности называется радиусом кривизны, а её центр С – центром кривизны кривой Г в точке М _о .

Заметим, что радиус кривизны вычисляется по формуле

(2.9)

(2.9’)

называется кривизной кривой Г.

2.5. НОРМАЛЬ И БИНОРМАЛЬ. РЕПЕР ФРЕНЕ

Определение 2.2 Главной нормалью кривой Г в точке М _о называется направленная прямая, идущая из точки М _о в центр круга кривизны.

Единичный вектор главной нормали находится по формуле:

(2.10)

или (2.10’)

Определение 2.3 Бинормалью кривой Г в точке М _о называется направленная прямая, проходящая через точку М _о и образующая вместе с положительной касательной и главной нормалью правую тройку, которая называется репером Френе (иногда — сопровождающим трёхгранником).

Единичный вектор бинормали находится по формуле:

(2.11)

или (2.11’)

Определение 2.4 Нормальной плоскостью называется плоскость, перпендикулярная касательной. Спрямляющей плоскостью называется плоскость, перпендикулярная главной нормали. Соприкасающейся перпендикулярная бинормали. Эти три плоскости иногда называют сопровождающим трёхгранником кривой.

2.6 ФОРМУЛЫ ФРЕНЕ

Единичные векторы касательной, нормали и бинормали связаны формулами Френе (без доказательства):

(2.12)

(2.13)

(2.14)

Здесь — кривизна, а величина

(2.15)

или (2.15’)

называется кручением кривой Г в точке М.

Точки, где кривизна кривой равна нулю, называются точками распрямления, а точки, в которых кручение равно нулю, называются точками уплощения.

Для того, чтобы кривая была плоской, необходимо и достаточно, чтобы кручение в каждой её точке было равно нулю.

2.7 ЭВОЛЮТА И ЭВОЛЬВЕНТА ПРОСТРАНСТВЕННОЙ КРИВОЙ

Определение 2.5 Эволютой  кривой Г: называется геометрическое место центров кривизны этой кривой.

Для получения уравнения эволюты  заметим, что ,

значит уравнение эволюты  имеет вид: (2.17)

Определение 2.6 Если кривая  является эволютой кривой Г, то кривая Г называется эвольвентой кривой  .

а) единичные векторы касательной, нормали, бинормали;

б) уравнения касательной, нормали и бинормали;

в) уравнения нормальной, соприкасающееся и спрямляющей плоскостей;

г) кривизну и кручение;

д) составить уравнение эволюты.

а) Точке М _о (1, 0, 0) соответствует значение параметра t _o =0. Найдём производные радиус-вектора в этой точке:

Найдём единичные векторы касательной, главной нормали и бинормали: ;

;

;

б) Поскольку вектор является направляющим вектором касательной, вектор — направляющим вектором главной нормали, а вектор — бинормали, запишем для точки М _о (1, 0, 0) канонические уравнения касательной:

главной нормали:

и бинормали: .

в) Нормальная плоскость проходит через точку М _о (1, 0, 0) перпендикулярно вектору касательной , её уравнение:

.

Соприкасающаяся плоскость проходит через точку М _о (1, 0, 0) перпендикулярно вектору бинормали , её уравнение:

.

Спрямляющая плоскость проходит через точку М _о (1, 0, 0) перпендикулярно вектору нормали , её уравнение:

.

г) Кривизна по формуле (2.9’):

.

Кручение найдём по формуле (2.15’):

Отсюда следует, что кривизна и кручение в точках винтовой линии имеют постоянное значение, .

д) Уравнение эволюты найдём по формуле (2.17): .

Здесь ; .

.

Подставим найденное в формулу (2.17):

,

т.е. эволютой винтовой линии будет так же винтовая линия, но повёрнутая вокруг оси Oz на 180  .

Видео:Уравнение касательной, параллельной заданной прямой.Скачать

Кривизна и кручение пространственной кривой. Формулы Френе

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Пусть 7 — регулярная кривая, Мо — точка кривой 7, П — плоскость, проходящая через касательную MoT кривой 7 в точке Мо. Пусть М — точка кривой 7, близкая к точке Мо, и Р — ортогональная проекция точки М на плоскость П (рис.31). Обозначим через h длину отрезка MP и через d — длину отрезка МоМ. Плоскость П называется соприкасающейся плоскостью кривой 7 в точке Мо, если отношение стремится к нулю при Геометрическое пояснение.

Среди всех плоскостей, проходяших через касательную к кривой в точке Мо, соприкасающаяся плоскость наиболее? есно прим ыкает к кривой в некоторой (малой) окрестности это Й точки. Пусть кривая 7 задана векторным уравнением и точка М0 кривой 7 отвечает значению to параметра. Если векторы неколлинеарны, то в точке Мо существует и притом ровно одна соприкасающаяся плоскость (рис. 32). Вектор г»(/о) Рис.32 второй производной вектора r(t) кривой лежит в соприкасающейся плоскости.

Поэтому соприкасающуюся плоскость кривой называют также плоскостью ускорений. Если кривая 7 задана в координатной форме Кривизна и кручение пространственной кривой Формулы Френе понятие гладкой поверхности Способы задания то уравнение соприкасающейся плоскости записывается в виде Нормаль кривой 7 в точке Мо, лежащая в соприкасающейся плоскости По кривой в этой точке, называется главной нормалью кривой в точке Мо, а нормаль кривой 7, перпендикулярная соприкасающейся плоскости По. называется бинормалью кривой 7 в точке Мо.

Плоскость, проходящая через касательную и бинормаль кривой 7 в точке Мо, называется спрямляющей плоскостью кривой 7 в точке Мо. Лрииар 1. Найти главную нормаль и бинормаль, соприкасающуюся и спрямляют ую плоскости аинтояой линии . Начнем с ураанаиия сопри касающейся плоскости. И МММ Так мак бинормаль перпендикулярна соприкасающейся плоскости , то ее каноничесяиа уравнения записываются следующим обр ааом:

Вычисли м теперь направляющий аактор главной нормали. Имеем Заменяя найден иый вектор на коллинеариый получаем канонические уравнения главной нормали : Наконец, — уравнение спрВмлющай плоосости , перпендикулярной главной нормали. (Первой) кривизной fcj кривой 7 в точке Мо называется предел отношения при М -» Мо, где ДА — наименьший угол между ка-сательн ыми к кривой 7 в ее точках Мо И М, а Да — длина дуги ^М0М (рис. 33).

Кривизна кривой измеряет скорость ее отклонения от касательн ой. Кривизна прямой равна нулю в каждой ее точке. /» Если — естественная параметризация кривой 7, то ее кривизна к вычисляется по формуле Вектор г»(«) называется вектором кривизны кривой. Он ортогонален единичному вектору касательной г'(«), а его длина равна кривизне кривой. .

В случае произвольной параметризации и кривизна2-регулярной кривой находится по формуле Пример 2. вектор кривизны винтовой линии Поэтому кривим винтов ой линии постол ни»: Пусть Мо — точка кривой у, отвечающая значению to естественного параметра, и — единичный вектор касательной кривой у в этой то же. Если точка Мо не является точкой распрямления кривой у» fciM/О.то формулой определен единичный вектор главной нормали кривой в этой точке.

Векторное произведение является единичным вектором бинормали кривой у (рис. 34).

В случае произвольнойпараметризаци и векторы t, п и b вычисляются по формулам Три луча, исходящие из точки М0 и имеющие направления, задаваемые векторами to, по и bo, образуют сопровождающий триэдр кривой у в точке Мо (рис. 34). Пример 3. Для винтовой линии b(,)= Обозначим через Д в наименьший угол между соприкасающимися плоскостями По и П кривой 7 в точке Мо и близкой ей точке М соответственно (этот угол совпадает с наименьшим углом ме.жду бинормалями кривой в точках А/о и М), а через Дз — длину дуги ^MqM кривой 7 (рис. 35).

Кручением к2 кривой 7 в точке М0 называется предел отношения ^ при , снабженный знаком в соответствии со следующим правилом выбора знаков: если векторы сонаправлены (они всегда коллинеарны), то выбирается знак (вращение соприкасающейся плоскости происходит от вектора п к вектору если векторы ип противоположно направлены, то выбирается знак « + » (вращение соприкасающейся плоскости происходит от вектора b к вектору п) (рис. 36).

Кручение кривой определено в любой точке 3-регулярной кривой, не являющейся точкой распрямления, и измеряет скорость отклонения кривой от соприкасающейся плоскости. Кручение плоской кривой равно нулю в каждой точке. Если Кривизна и кручение пространственной кривой Формулы Френе понятие гладкой поверхности Способы задания — естественная параметризация кривой, то ее кручение вычисляется по формуле В случае произвольной параметризации имеем Пример 4.

Возможно вам будут полезны данные страницы:

Кручение винтовой линии постоянно

Вектор Дарбу является вектором мгновенной угловой скорости сопровождающего трехгранника при движении точки по кривой с единичной скоростью. Пример 8. Вектор Дарбу винтовой линии •параллелен оси винтовой линии (рис. 37). Единичные векторы касательной главной нормали п(«) и бинормали b(e) кривой 7 и ее кривизна к(в) и кручение ki(a) в каждой точке связаны соотно шениями называемыми уравнениями Френе. «

Выберем в пространстве прямоугольную декартову координ етную систему Охух так, чтобы начало координат — точка О — совпадало с точкой Мо кривой 7, отвечающей энрч ению «о = 0 естественного параметра, а ортами координатных осей Ох, Оу и Ох были единичные векторы Раскладывая векторную функцию г(в) в окрестности точки «о = 0 по степеням * и сохраняя лишь главные члены, получимуравнения кривойблизкой кривой 7:

Где Записывая последние соотношения в координатной форме и предполагая , убеждаемся в том, что проекции кривой общий вид которой показан на.рис.38, на координатные плоскости имеют следующий вид (рис. 39): на соприкасающуюся плоскость (рис. 39 а); на спрямляющую плоскость (рис. 39 б); на нормальную плоскость (рис. 39в). §5. Понятие гладкой поверхности.

Способы задания Пусть I? — ограниченная плоская область, 0D — ее граница и I) = D U 6D — оамыка ние области Д, Введем на плоскости координатную систему (u, v) и зададим на множестве Ъ три непрерывные функции с Пусть ж прямоугольные декартовы координаты точек в трехмерном евклидовом пространстве R3.

обладают следующим свойством: Сюйстю А. Если — различные точки множества!?» тоточки пространства R1, координаты которых вычисляются по формулам также различны. Определение. Множество 5 точек Af, координаты у и * которых определяются соотношениями (1) и функции ) обладают свойством А, называется простой поверхностью (рис. Множество точек М с координатами , — образ границы QD области D — называется границей простой поверхности 5.

Овоаиечение:

Соотношения (1) называются параметрическими уравнениями простой поверхно- сти. . Пример 1. График непрерывной функции является примером простой поверхности (рис. 41). Ее параметрические уравнения имеют вид одеФяап ып яктеодг — Пусть I, J и к — орты координатных осей. Тогда задание поверхности 5 при помощи фунхиий (1) равносильно заданию одной векторной функции — В этом случае говорят, что поверхность S задана векторным уравнением.

Простая поверхность 5 называется гладкой в точке Мо, отвечающей значениям и параметров, если функции имеют д точке («о, ^ непрерывныепроизводные. v Точка Ма гладкой поверхности 5 называется обыкновенной, или регулярной, если В противном случае точк!» А/о называется особой. , Поверхность называется регулярной, если условие (3) выполняется в каждой ее точке. Часто условие (3) удобнее записывать в равносильной форме Пример 2.

График гладкой функции является регулярной поверхностью, так как всегда Пример 3. У конической поверхности, задаваемой уравнениями все точки, кроме точки 0(0,0,0) (при и = 0, v — 0), регулярна (рис.42). В точке О имеем Другим распространенным способом задания поверхности является неявный способ задания поверхности какмножества 5 точек М .координаты х,уиг которых обращают в тождество уравнение Кривизна и кручение пространственной кривой Формулы Френе понятие гладкой поверхности Способы задания

Если гладкая фунщия своих аргументов, причем , то поверхность 5 будет регулярной. Пример 4. Сфера является регулярной поверхностью: в каждой точке. Пусть 5 — простая поверхность, Мо и М — различные ее точки. Плоскость П, проходящая через точку Мо, называется касательной к поверхности 5 в точке Мо, если при стремлении переменной точки М к точке Мо (по произвольному закону) угол между прямой МоМ и плоскостью П сгремится к нулю (рис. 43).

Пусть — векторное уравнение регулярной поверхности 5 и М0 — точка поверхности 5, отвечающая значениях! ио и v0 параметров и и v. Вычислим векторы ru(uo, vo) и г„(и0, vo), отложим их от точен Мо и проведем через точку Мо плоскость П, содержащую эти векторы. Построенная плоскость П будет касательной плоскостью поверхности в точке М0 (рис. 44), В каждой точке регулярной поверхности существует и притом ровно одна касательная плоскость.

Прямая, проходящая через точку Мо регулярной поверхности 5 и пер-пендакулярная касательной плоскости поверхности в этой точке, называется нормалью к поверхности 5 в точке М0; — вектор нормали. Рнс. 44 Пример S. Написать уравнения касательной плоскости и нормали поверхности, заданной уравнением Вычислим вектор нормали в точке Л/о- Имеем равнение касательной плоскости поверхности в точке (х

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

📸 Видео

найти уравнение касательной к эллипсуСкачать

Касательная плоскость и нормаль к поверхностиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать