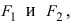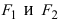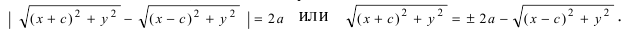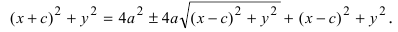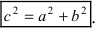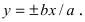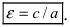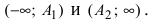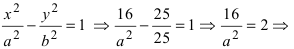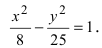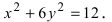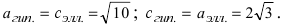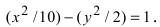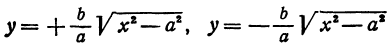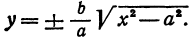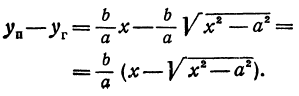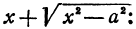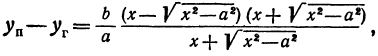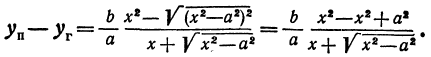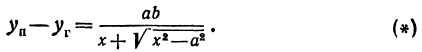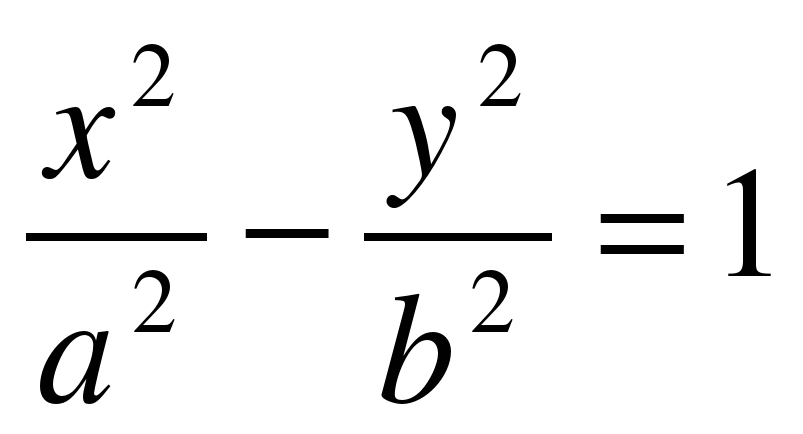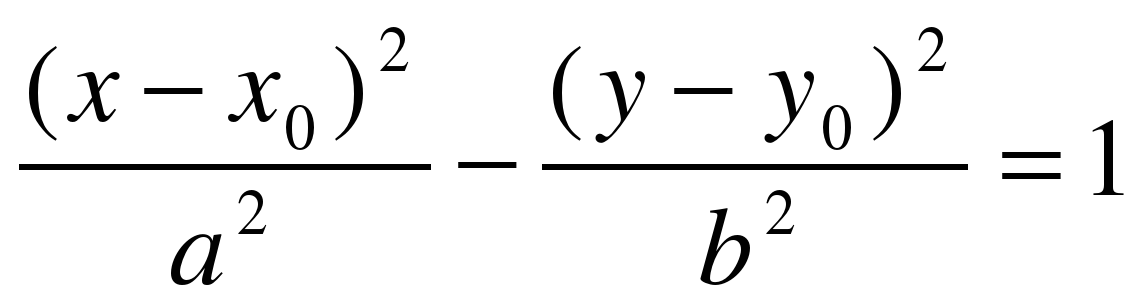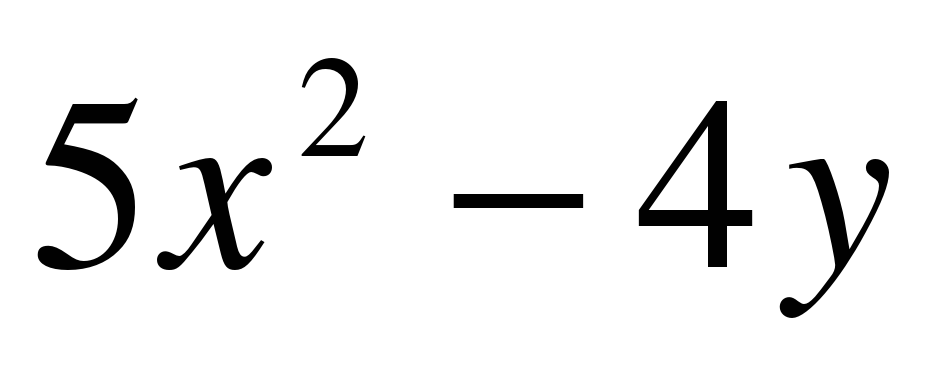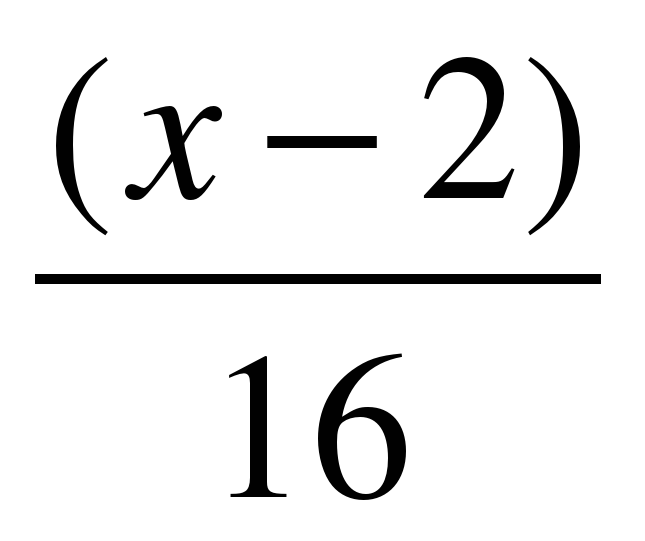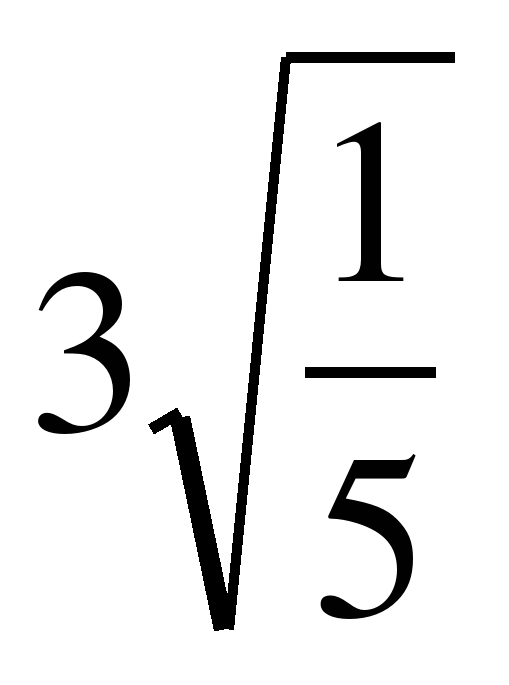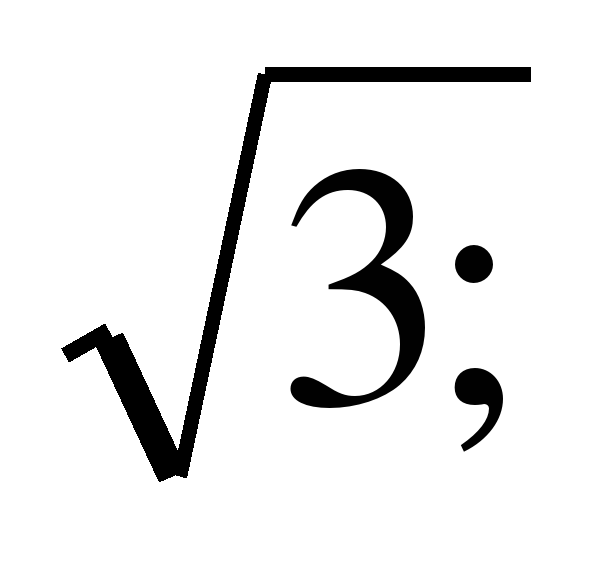Гипербола проходит через точки и
. Найти уравнение гиперболы.
может быть записано так
Определению подлежат a 2 и b 2 . Подставим в это уравнение координаты первой точки и получим
Подставляя в уравнение гиперболы (1) координаты второй точки, получим
Решим систему уравнений
Умножая первое уравнение на 4, а второе на 3 и вычитая из второго первого, получим a 2 = 5. Подставим a 2 = 5 в первое уравнение и получим 20b 2 — 45 = 5b 2 , откуда b 2 = 3. Подставляя найденные значения a 2 и b 2 в (1), получим, что искомое уравнение имеет вид
Видео:§22 Исследование канонического уравнения гиперболыСкачать

Гипербола — определение и вычисление с примерами решения
Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
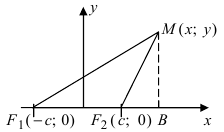
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 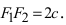
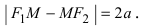
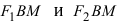
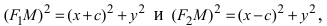
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 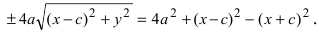
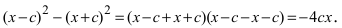
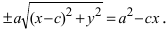
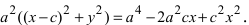
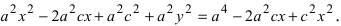
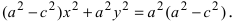
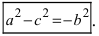
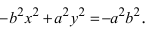
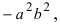
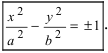
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 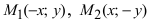
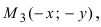
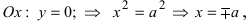
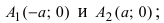
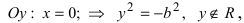
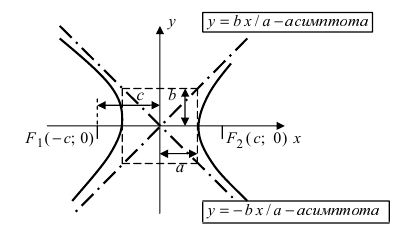
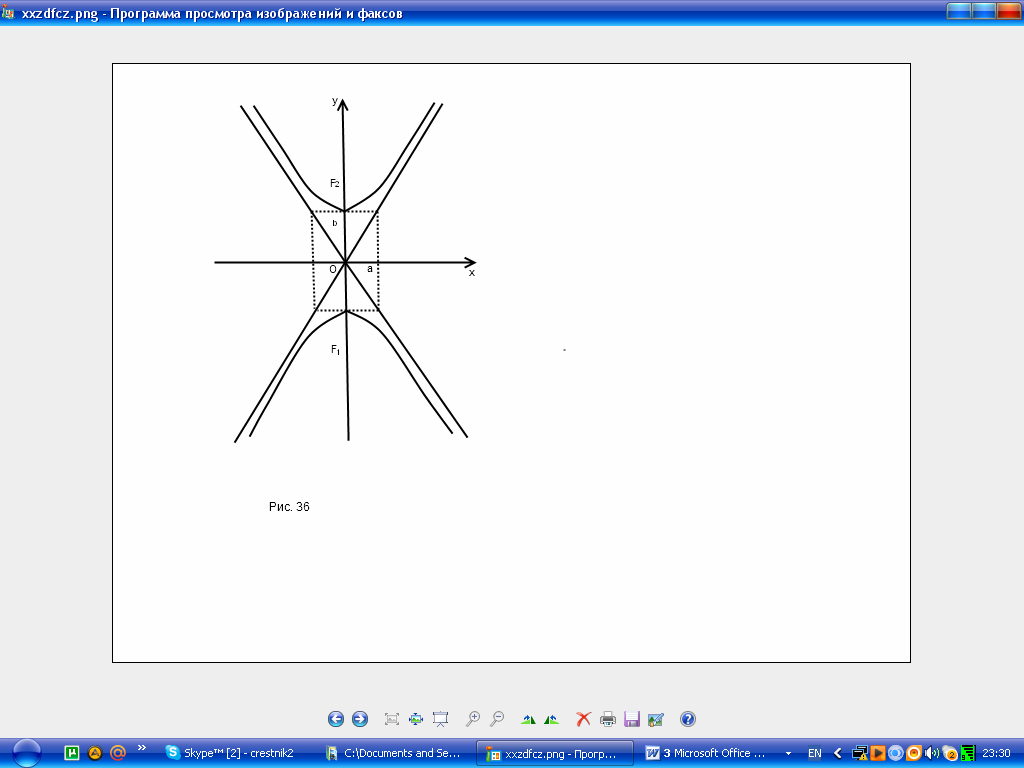
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 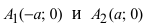
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 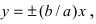
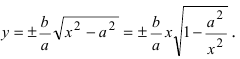
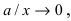
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b — мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 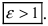
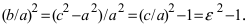
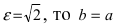
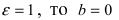
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
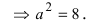
Пример:
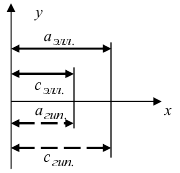
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 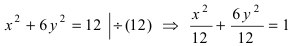
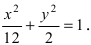
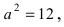
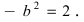
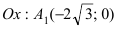
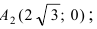
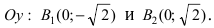
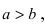
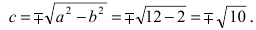
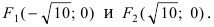
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 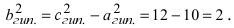
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Гипербола в высшей математике
Решая его относительно 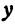
или одну двузначную функцию
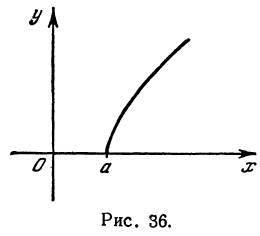
Функция 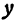

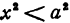
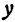
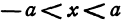
При 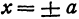
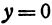
При 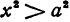
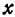
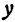
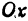
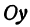
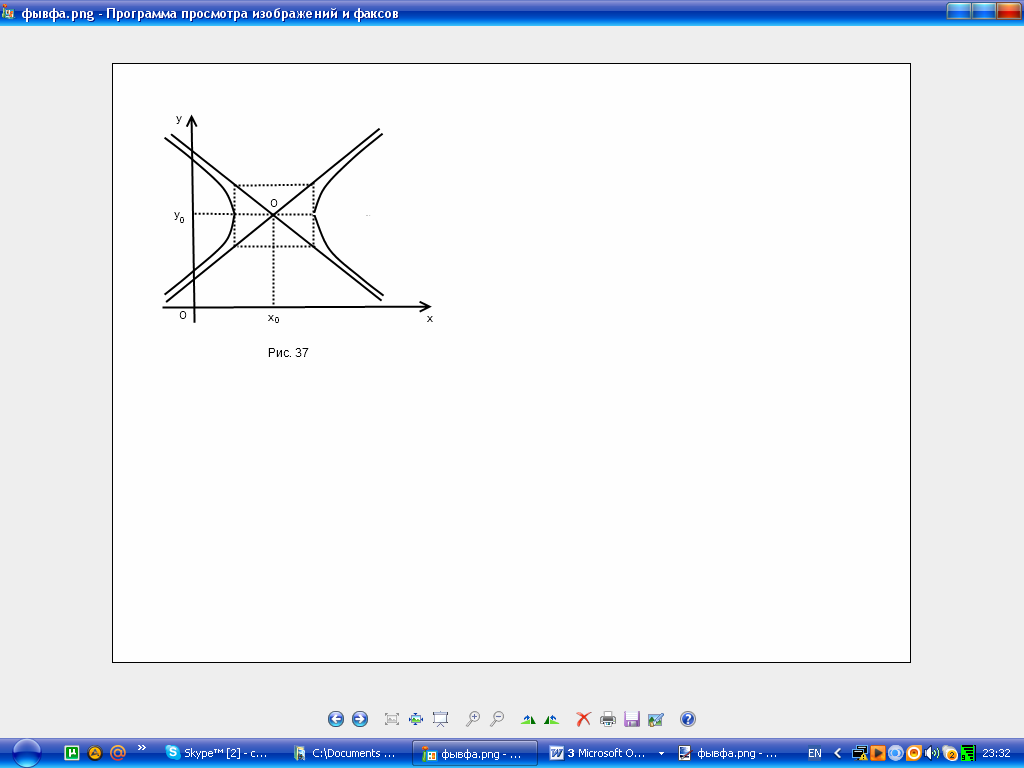
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
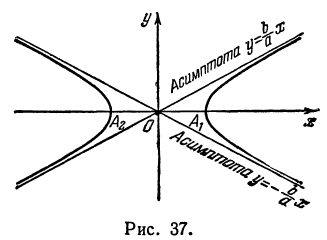
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 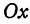
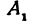
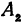
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
Рассмотрим прямую, заданную уравнением 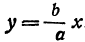
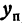
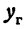
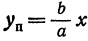
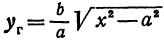
Умножим и разделим правую часть на
Будем придавать 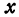
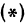

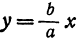
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 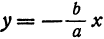
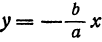
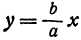
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Видеоурок "Гипербола"Скачать

Гипербола
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек этой же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Просмотр содержимого документа
«Гипербола»
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек этой же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Коническое уравнение гиперболы :
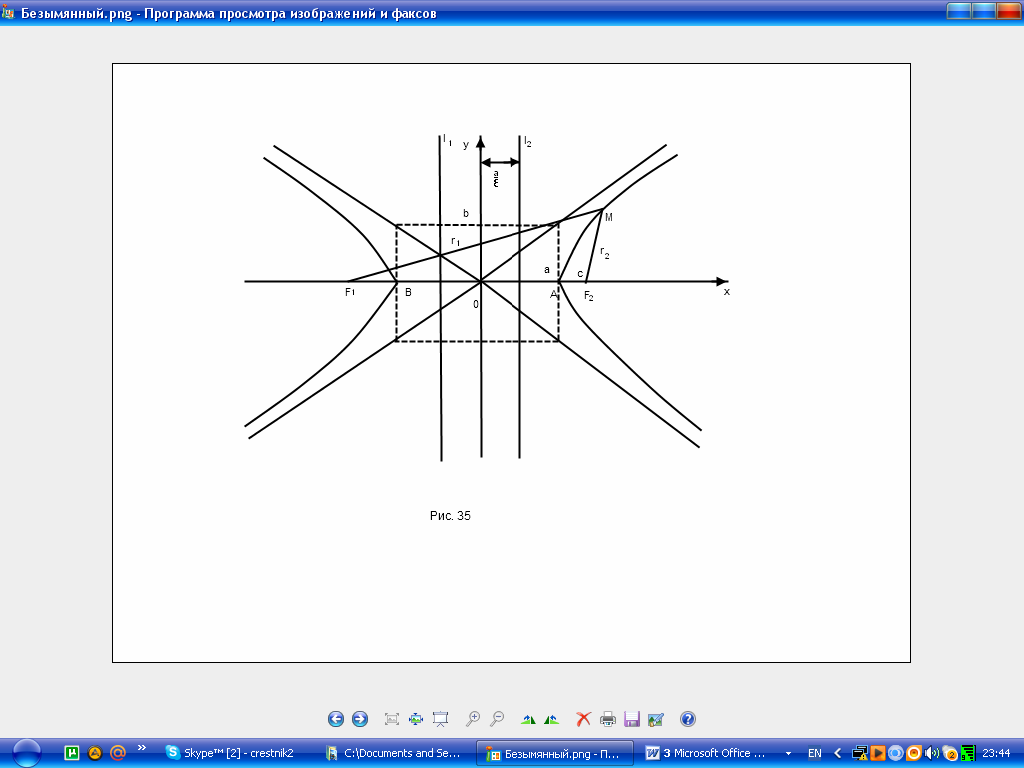
где а – действительная, b – мнимая полуось гиперболы. Числа 2а и 2b называются соответственным действительной и мнимой осями гиперболы. Координаты фокусов : F1(- с;0),F2(c;0), с – половина расстояния между фокусами(рис.35).Числа а, b и c связаны соотношением
Точки А и В называются вершинами гипербол, точка О – центром гиперболы, расстояние r1 и r2 от произвольной точки М гиперболы до фокусов называются фокальными радиусами этой точки
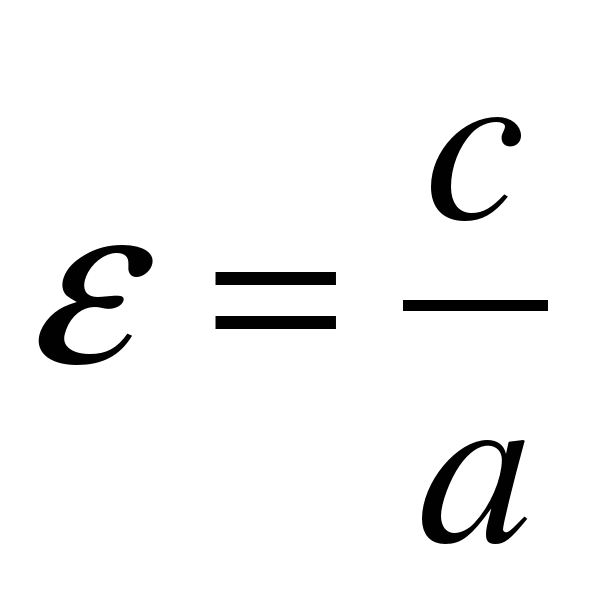
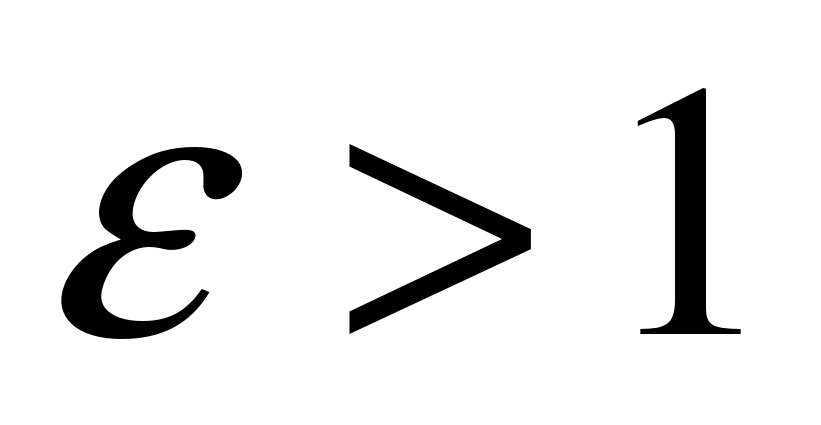
Называется эксцентриситетом гиперболы.
Фокальные радиусы определяются формулами : для точек первой величины гиперболы:
r1 = a + 

для точек любой ветви:
r1 = — a + 
Прямоугольник, центр которого совпадает с точкой Щ, а стороны равны и параллельны осям гиперболы называется основным прямоугольником гиперболы. Диагонали основного прямоугольника гиперболы лежат на двух прямых, называемых асимптотами гиперболы; они определяются уравнениями
y = 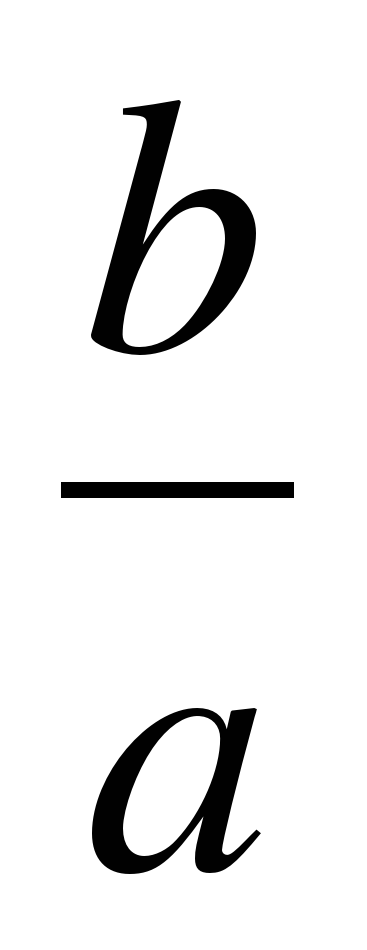
Две прямые l1 и l2, параллельные мнимой оси гиперболы и отстоящей от нее на расстоянии, равном 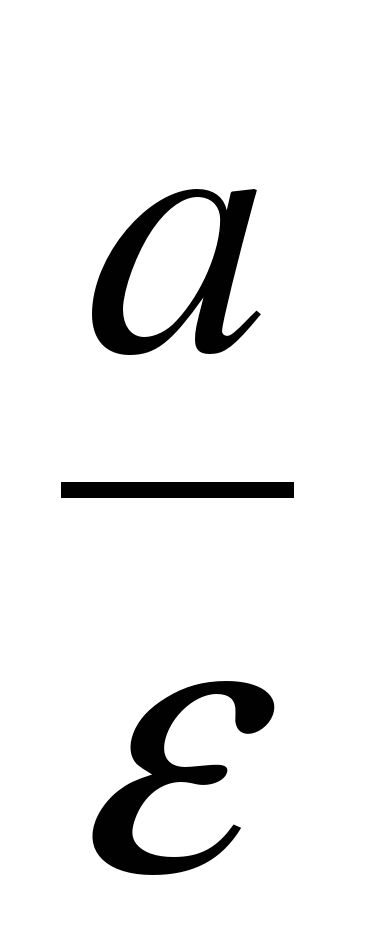
x = 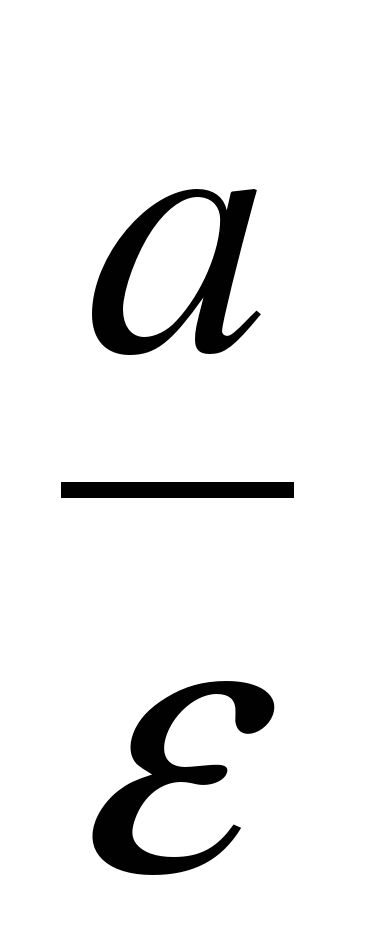
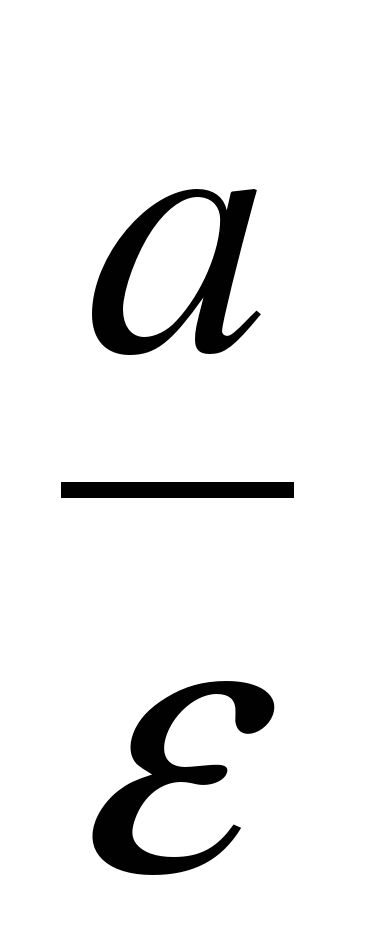
Замечания, 1) Если a = b, то гипербола (3.12) называется равносторонней ( равнобочной). Ее уравнение принимает вид
2) если фокусы гиперболы лежат на оси Оy, то уравнение гиперболы имеет вид
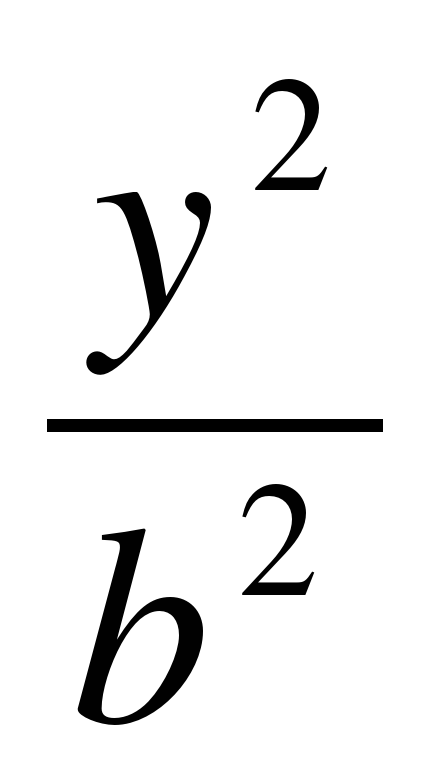
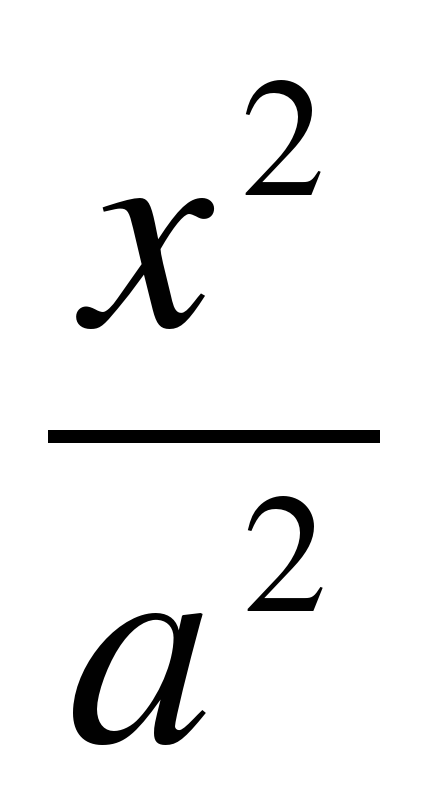
Эксцентриситет этой гиперболы равен 
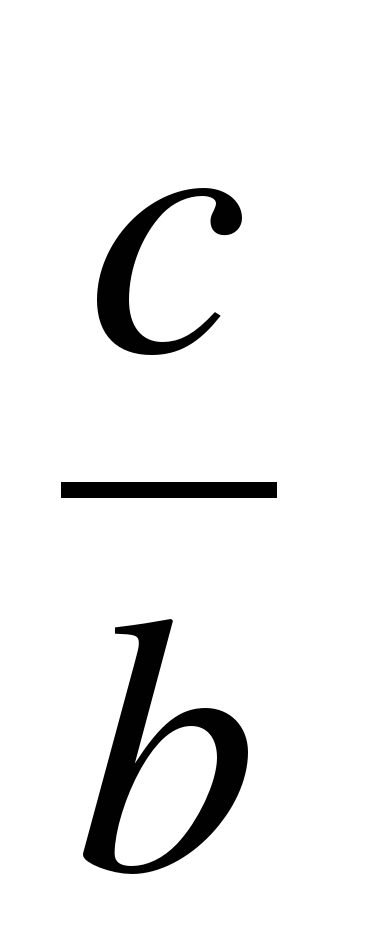
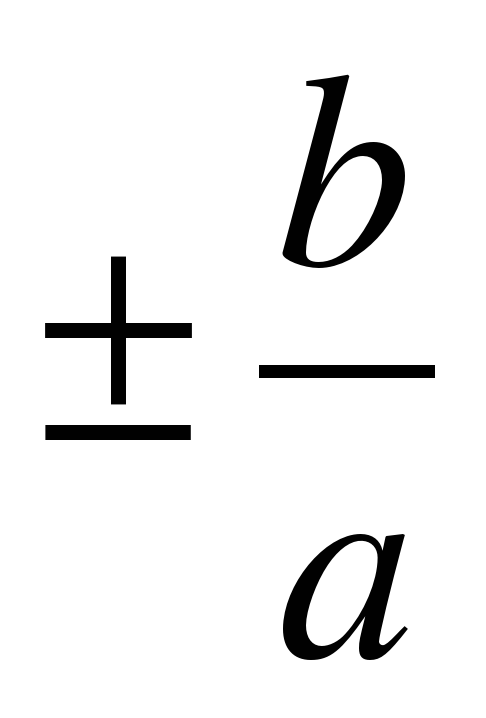
А уравнение директрис y = 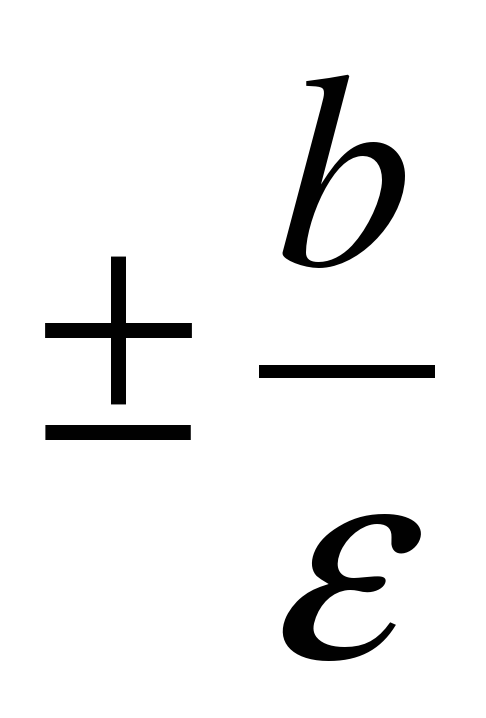
3) уравнение гиперболы с осями, параллельными координатным, имеет вид

Задания для практических занятий:
1. Дано уравнение гиперболы 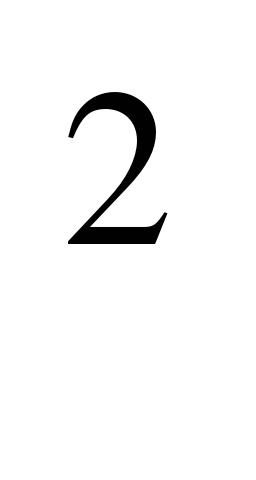
1) длины его полуосей;
2) координаты фокусов;
3) эксцентриситет гиперболы;
4) уравнения асимптот и директрис;
5) фокальные радиусы точки М (3;2,5)
2. Составить уравнение гиперболы, если ее фокусы лежат на оси Оу и расстояние между ними равно 10, а длина действительной оси равна 8.
3. Составить каноническое уравнение гиперболы, если:
3) в=6;, уравнения асимптот у=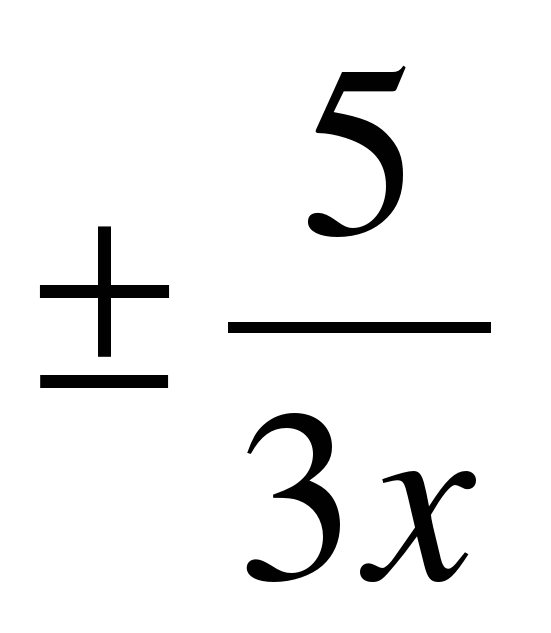
4.Найти уравнение гиперболы, фокусы которой находятся в точках F1 (-2;4) и F2 (12;4),
а длина мнимой оси равна 6.
5. Найти каноническое уравнение гиперболы с фокусами на оси Ох, проходящей через точки М1 (6;-1) и М2 (-8;-2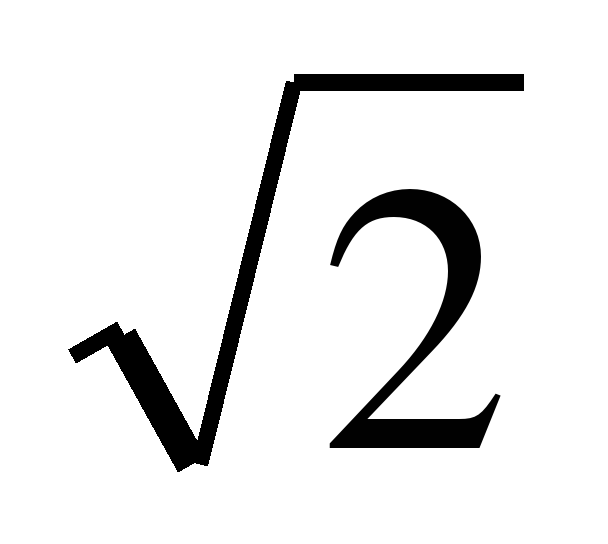
6. Составить уравнения асимптоты гиперболы . 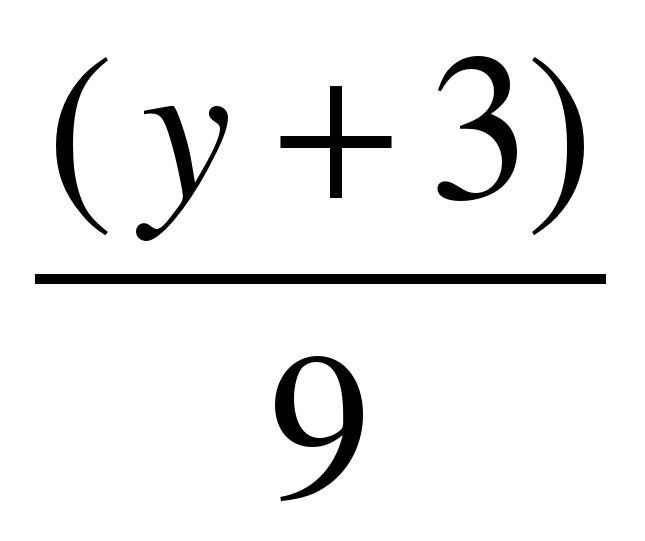
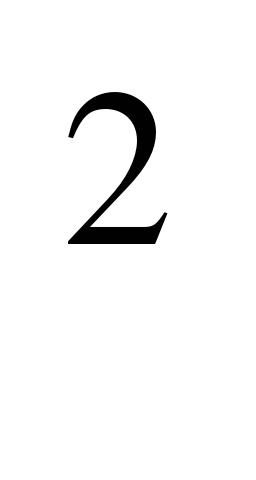
7. Дан эллипс 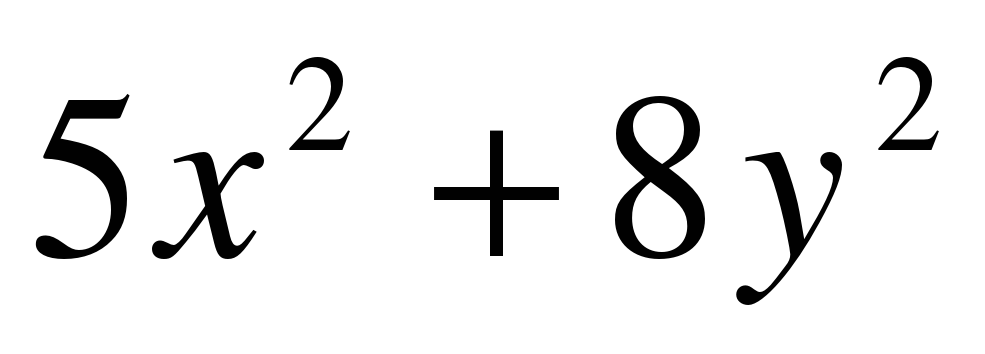
8. Составить уравнение равносторонний гиперболы с фокусами на оси Ох, если гипербола проходит через точку: 1) А (-5;4); 2) В (8;2)
Задания для самостоятельной работы.
1. Составить уравнение гиперболы, если ее вершины находятся в точках
2. Составить уравнение гиперболы, если ее асимптоты заданы уравнениями у= 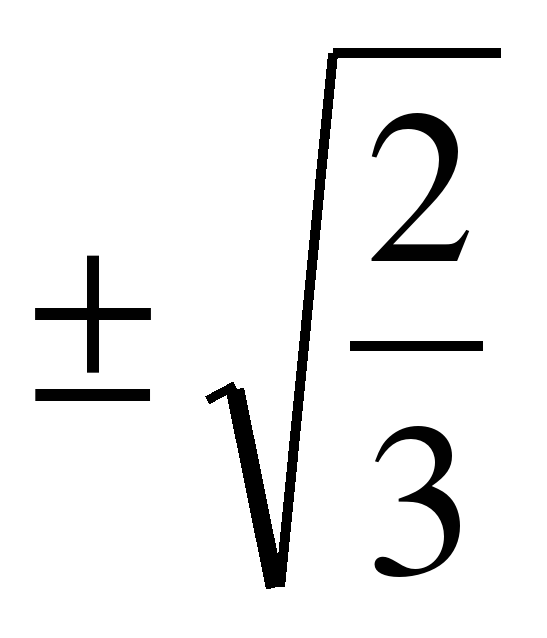
3. Составьте уравнение гиперболы с фокусами на оси Ох, если:
1) длины ее действительной оси равна 6, а эксцентриситет равен 5/3;
2) длина мнимой оси равна 8, а эксцентриситет равен
4. Написать каноническое уравнение гиперболы, если:
1) с=10 и уравнение асимптот у=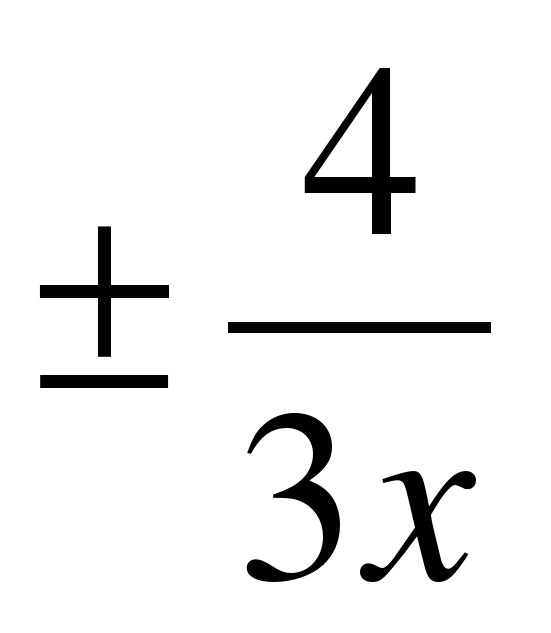
2) Е= 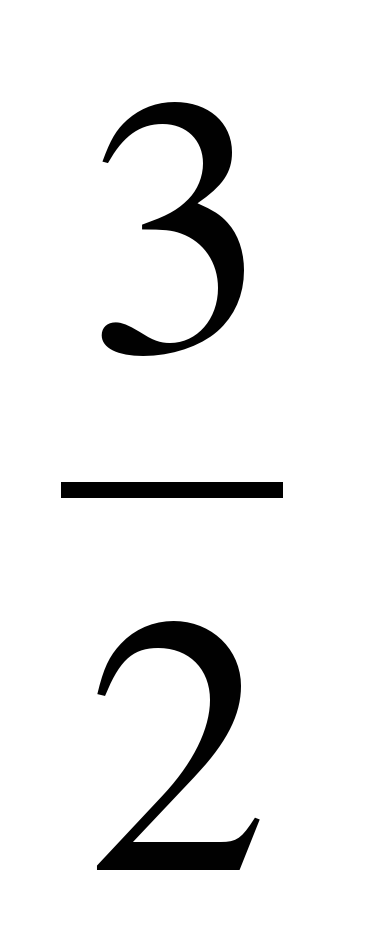
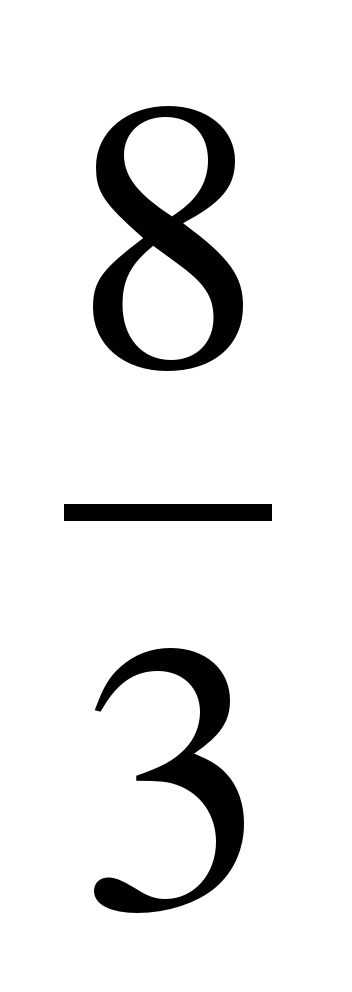
3) Е = 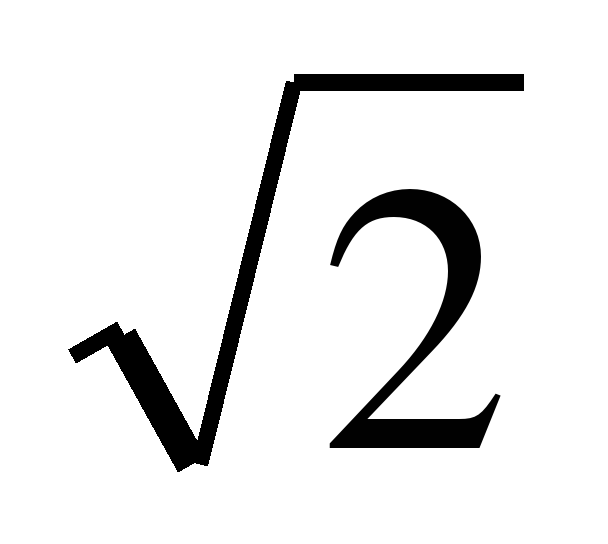
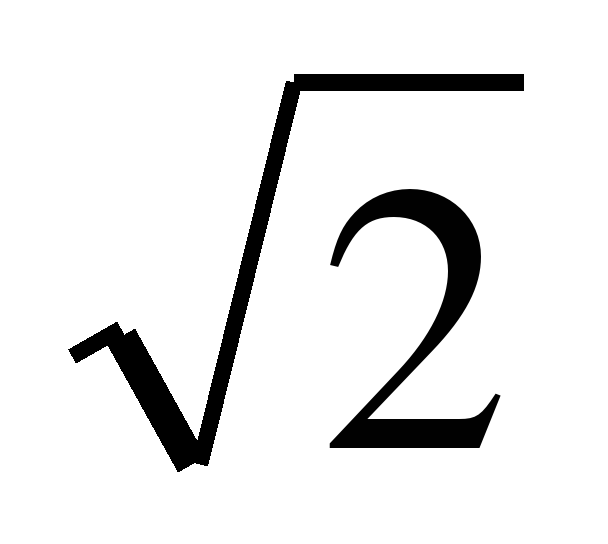
5. Найти уравнение гиперболы, симметричной относительно осей координат, зная, что ее мнимая полуось равна 2 и гипербола проходит через точку М (4; 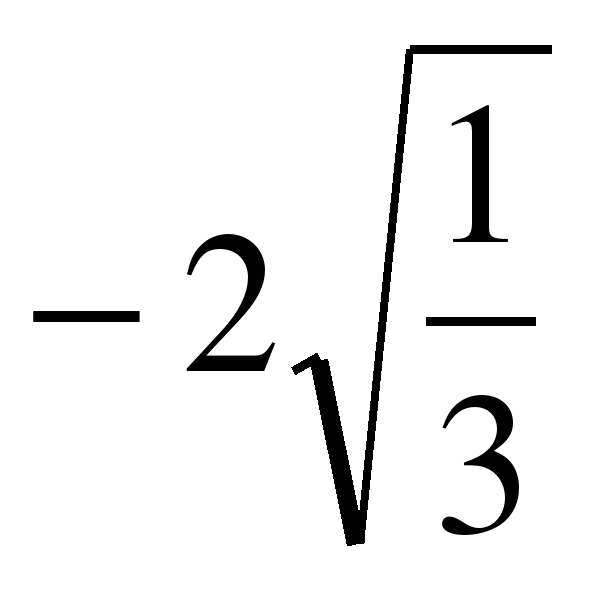
6. Составить уравнение равносторонней гиперболы с фокусами на оси Оу, если гипербола проходит через точку (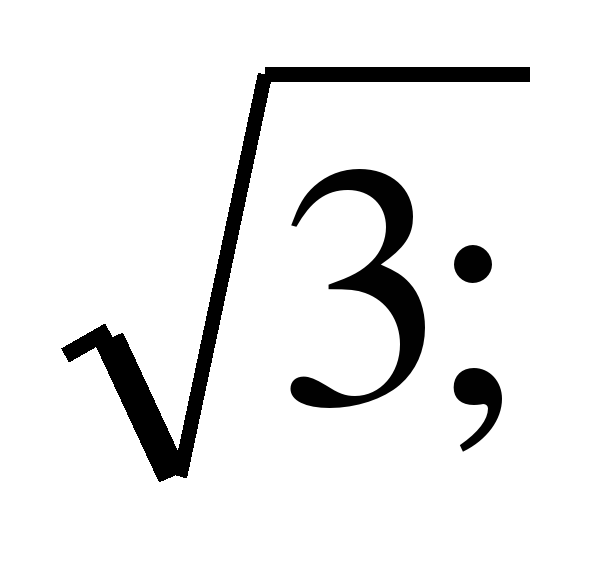
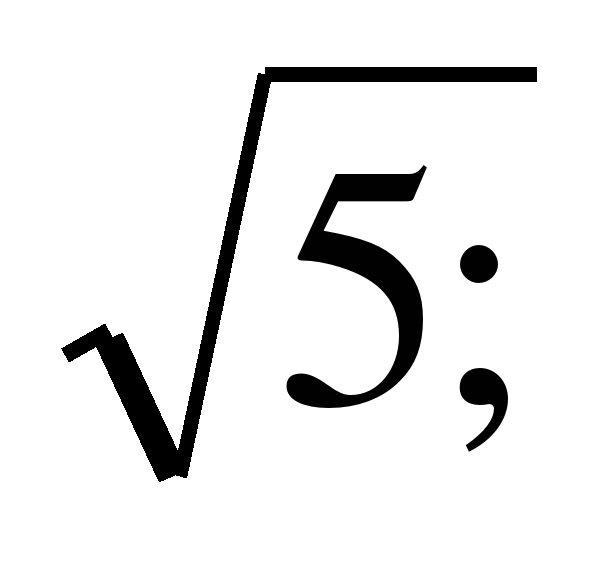
7. Дана гипербола 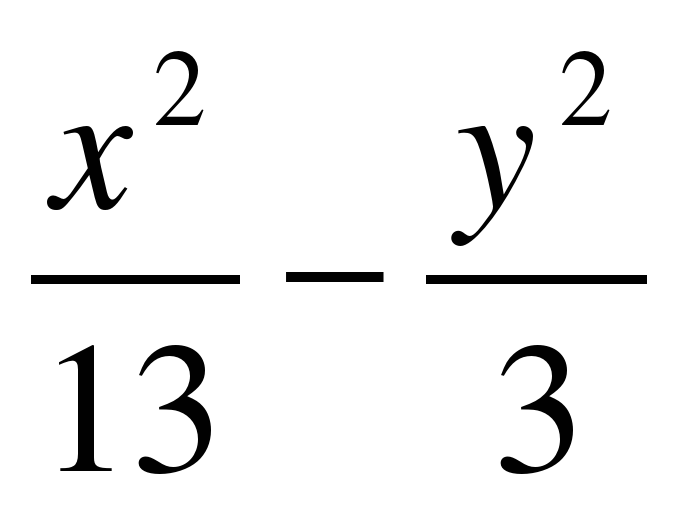
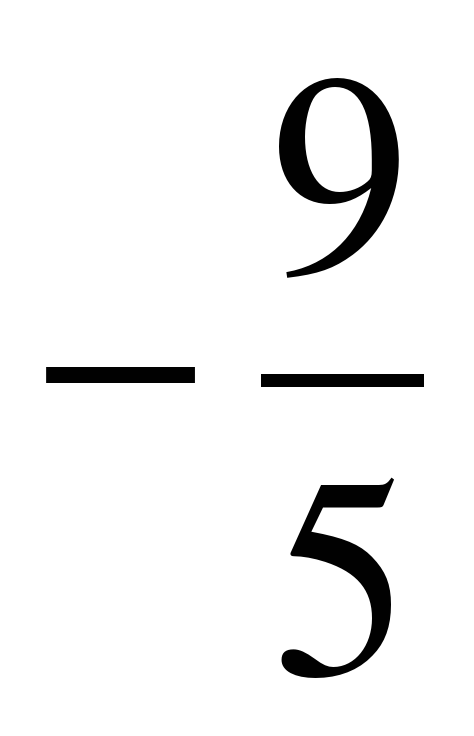
8. На гиперболе 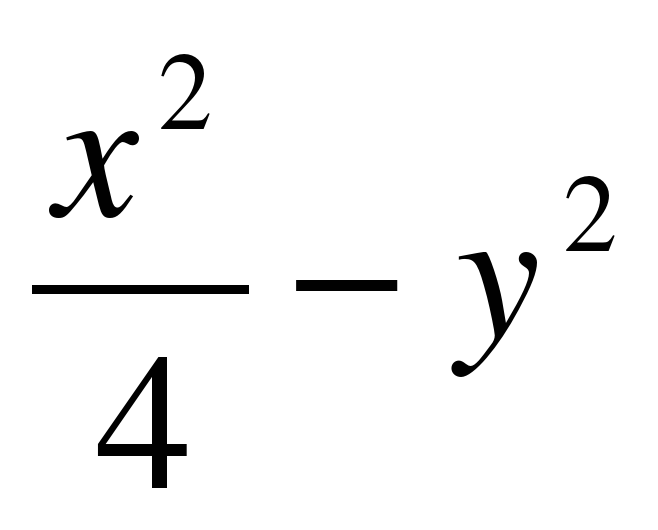
Ответы к заданиям для самостоятельного решения:
1.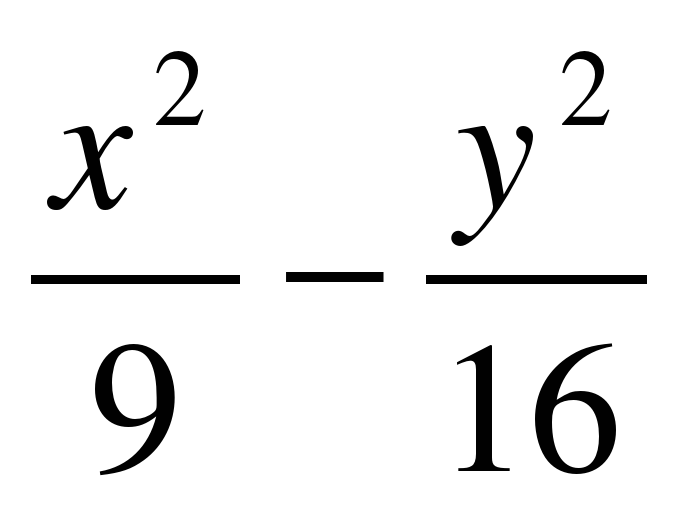
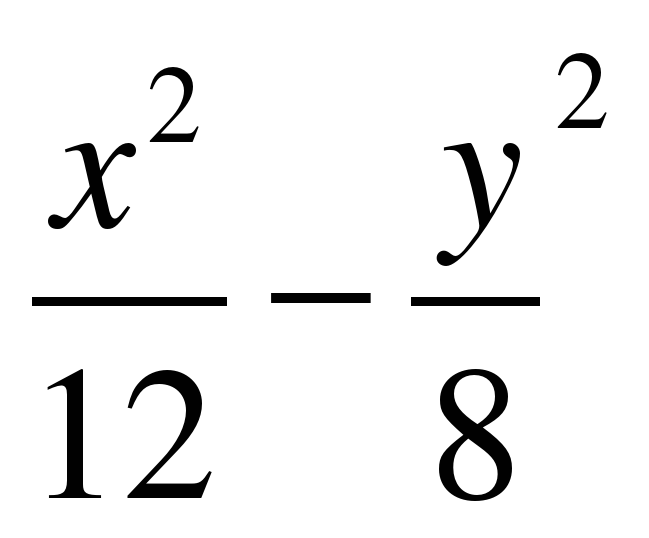
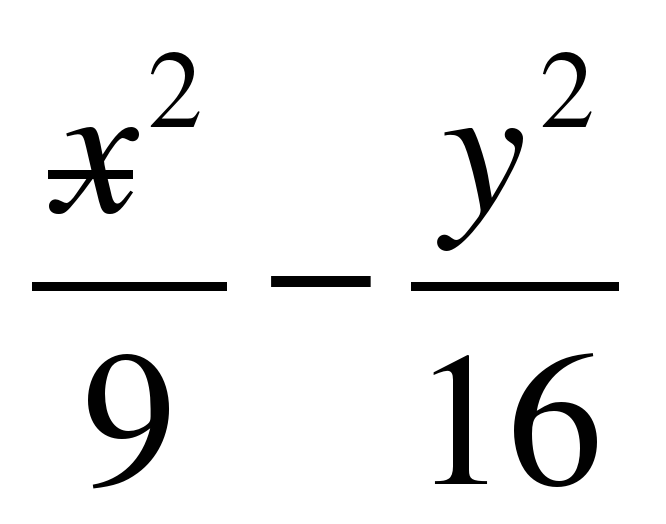
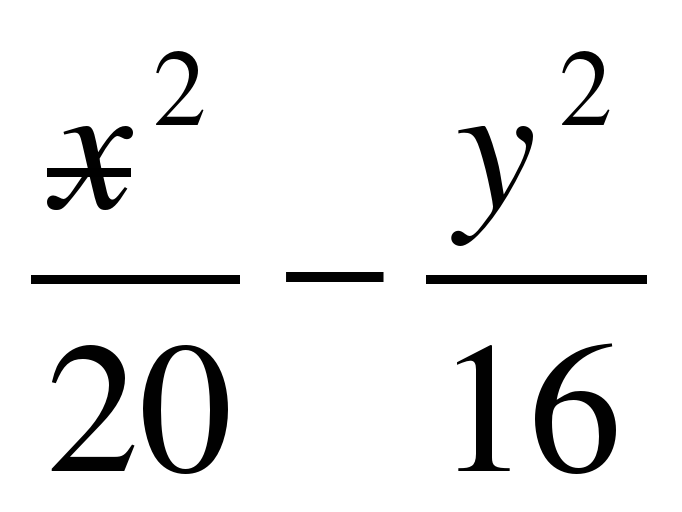
Видео:ГиперболаСкачать

№1. Найти точки пересечения асимптот гиперболы х²-3у²=12 с окружностью,имеющей центр в правом фокусе гиперболы и проходящей через начало координат.
№2. Гипербола проходит через точку М(6; 3√5/2),симметрична относительно осей координат и имеет вещественную полуось а=4. Написать уравнения перпендикуляров ,опущенных из левого фокуса гиперболы на ее асимптоты.
С подробным решением и объяснением ,пожалуйста! 🙂
💥 Видео
Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Овчинников А. В. - Аналитическая геометрия - Эллипс, гипербола, параболаСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

§29 Эксцентриситет гиперболыСкачать

Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Гипербола (часть 7). Директрисы гиперболы. Высшая математика.Скачать

ЭллипсСкачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

§23 Построение гиперболыСкачать

187. Гипербола.Скачать

Математический анализ, 15 урок, АссимптотыСкачать