Найти уравнение эллипса и эксцентриситет если 2а 12 а директрисы заданы уравнениями x 12

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Понятие о кривых второго порядка

Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.

Общий вид уравнения кривой второго порядка следующий:

,

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.

При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.

Видео:§28 Эксцентриситет эллипсаСкачать

Эллипс, заданный каноническим уравнением

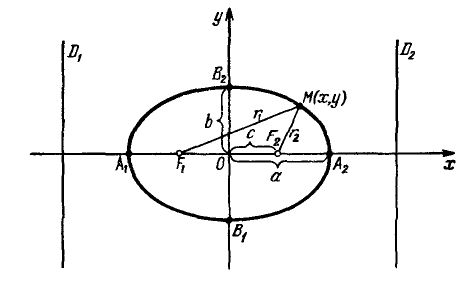
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

Фокусы обозначены как и на рисунке ниже.

Каноническое уравнение эллипса имеет вид:

,

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .

Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

.

Точки и , обозначенные зелёным на большей оси, где

,

называются фокусами.

называется эксцентриситетом эллипса.

Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,

— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

Результат — каноническое уравнение эллипса:

.

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

.

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .

Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

.

Получаем фокусы эллипса:

Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Решить задачи на эллипс самостоятельно, а затем посмотреть решение

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) расстояние между фокусами 30, а большая ось 34

2) малая ось 24, а один из фокусов находится в точке (-5; 0)

3) эксцентриситет , а один из фокусов находится в точке (6; 0)

Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Продолжаем решать задачи на эллипс вместе

Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

.

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

,

называются директрисами эллипса (на чертеже — красные линии по краям).

Из двух вышеприведённых уравнений следует, что для любой точки эллипса

,

где и — расстояния этой точки до директрис и .

Пример 7. Дан эллипс . Составить уравнение его директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:

.

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

.

Теперь можем получить и квадрат длины меньшей полуоси:

Уравнение эллипса готово:

Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

.

Получили единицу, следовательно, точка находится на эллипсе.

Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:

Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

,

так как из исходного уравнения эллипса .

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

Видео:Видеоурок "Гипербола"Скачать

Математический портал

Видео:Кривые второго порядкаСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Эллипс.

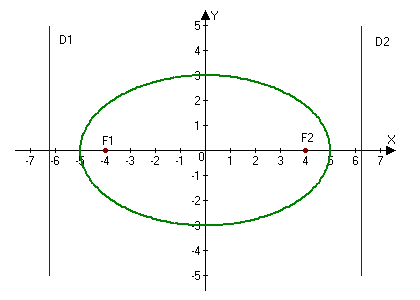
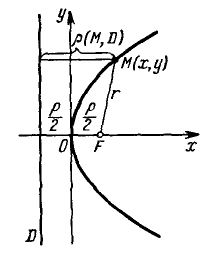
Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.

Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.

Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.

Теорема. ( Директориальное свойство эллипса)

Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$

Примеры.

2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.

Приведем уравнение эллипса к каноническому виду:

а) Находим полуоси $a=5,$ $b=3.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$

$c=sqrt=sqrt=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$

г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac;$ г) $D_1: x=-frac$ и $D_2: x=frac.$

2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.

Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:

Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-frac=-frac $ и $D_2: x=frac=frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$

2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.

Решение.

Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$

Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$

Таким образом, уравнение эллипса $frac+frac=1.$

Далее найдем координаты фокусов:

$c=sqrt=sqrt=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$

Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$

Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$

Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$

расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$

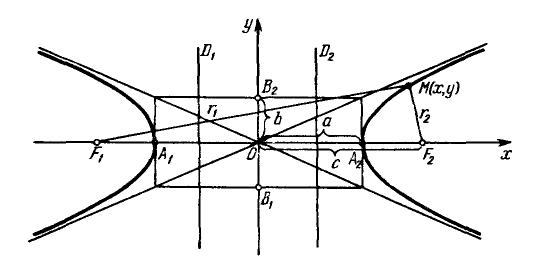
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.

Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.

Теорема. (Директориальное свойство гиперболы).

Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$

Примеры.

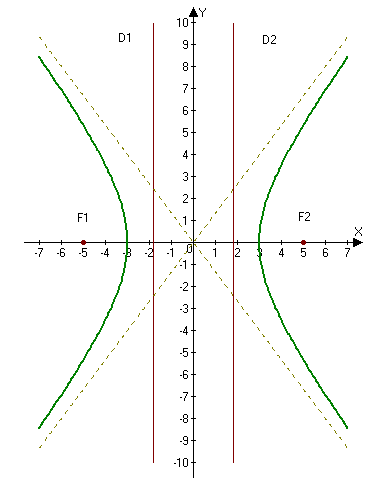
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.

Приведем уравнение гиперболы к каноническому виду:

а) Находим полуоси $a=3,$ $b=4.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$

$c=sqrt=sqrt=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$

г) Асимптоты гиперболы находим по формулам $y=pmfracx:$

д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac;$ г) $y=pmfracx;$ д ) $D_1: x=-frac$ и $D_2: x=frac.$

2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.

Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:

Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$

Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$

$$y+3=frac(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$

$$y+3=-frac(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-frac=-frac $ и $D_2: x=frac=frac.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$

2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac-frac=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.

Решение.

Проверим, что заданная точка лежит на гиперболе:

Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac-frac=1.$

Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:

$c=sqrtRightarrow c=sqrt=sqrt =5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$

Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$

Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-fracRightarrow x=-fracRightarrow 5x+16=0;$

$D_2: x=fracRightarrow x=fracRightarrow 5x-16=0;$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$

Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$

расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$

Ответ: $r_1=9/4,$ $r_2=frac;$ $d_1=frac;$ $d_2=frac.$

2.273. Найти точки гиперболы $frac-frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$

Решение.

Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt=sqrt =5.$

Отсюда находим $F_1=(-5, 0).$

Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$

Чтобы н айти точки гиперболы $frac-frac=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений

Решим уравнение $5x^2+18x-72=0:$

Находим соответствующие координаты $y:$ $y_1=pmsqrt=sqrt$ — нет корней .

Ответ: $(-6, pm4sqrt 3).$

Парабола.

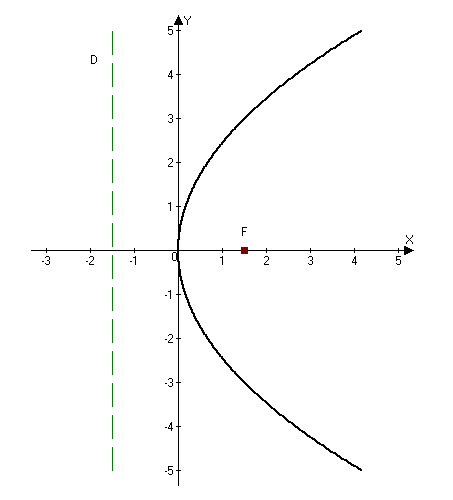
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.

Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.

Точка $Fleft(frac

, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.

Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.

Примеры.

2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.

Решение.

Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $

$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$

Ответ: $p=3.$

2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$

Решение.

Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:

Ответ: $y^2=-x.$

2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$

Решение.

Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$

Приведем заданное уравнние к такому виду:

Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$

Ответ: $C(0, 2),$ $p=2.$

2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$

Решение.

Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$

Таким образом, точка $M$ имеет координаты $(3, 6).$

Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$

Далее находим фокальный параметр точки:

Ответ: $6.$

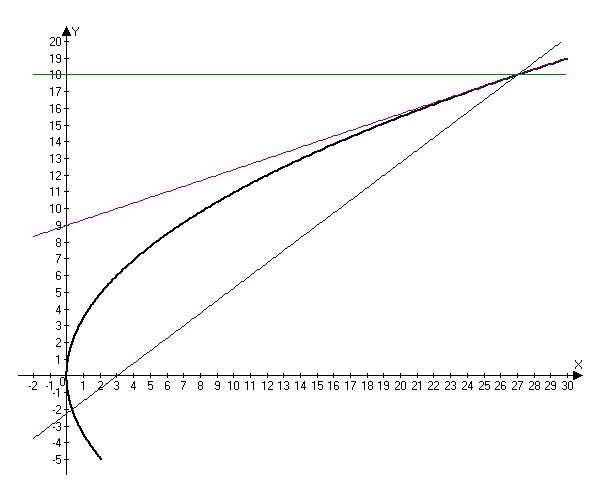
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.

Решение.

Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$

Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$

Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac.$

Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$

$0=fraccdot 3+bRightarrow b=-frac.$ Таким образом, уравнение луча, направленного из фокуса $y=fracx-frac.$

Далее, найдем точку пересечения найденной прямой с параболой:

Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac=frac=27.$

Таким образом, луч пересекает параболу в точке $(27, 18).$

Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$

Подставляем все найденные значения в уравнение касательной:

$y-18=frac(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$

Далее, найдем угол $beta$ между лучем $y=fracx-frac$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac$

$$L_2: x-3y+27=0Rightarrow y=fracx+9Rightarrow k_2=frac.$$

Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$

Зная $tgbeta=frac$ и $tgalpha=k_1=frac$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$

$$tg(2beta-alpha)=frac=frac<frac-frac><1+fracfrac>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Дан эллипс 9x² + 25y² = 225 найти а) его полуоси б) фокусы в) эксцентриситет г) уравнения директрис?

Математика | 10 — 11 классы

Дан эллипс 9x² + 25y² = 225 найти а) его полуоси б) фокусы в) эксцентриситет г) уравнения директрис.

Каноническое уравнение эллипса

Представим уравнение эллипса в каноническом виде.

Для этого обе части равенства разделим на 225 и в знаменателях дроби выделим квадраты.

Полуоси эллипсаа = 5, b = 3.

Полуоси и фокусное расстояние связаны следующим равенством

Фокусы эллипса : F₁ (4 ; 0), F₂ ( — 4 ; 0).

Эксцентриситет вычисляется по формуле :

Эксцентриситет эллипса : ε = 4 / 5

Уравнения директрис эллипса находятся по формуле :

Уравнения директрис эллипса : d₁ : х = 6, 25, d₂ : х = — 6, 25.

Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Дан эллипс x ^ 2 / 7 + y ^ 2 / 16 = 1?

Дан эллипс x ^ 2 / 7 + y ^ 2 / 16 = 1.

Найдите его эксцентриситет.

Видео:166. Найти каноническое уравнение эллипса.Скачать

Записать уравнение окружности, проходящей через фокусы эллипса 24х2 + 25у2 = 600 и имеющей центр в точке А(0 ; 6)?

Записать уравнение окружности, проходящей через фокусы эллипса 24х2 + 25у2 = 600 и имеющей центр в точке А(0 ; 6).

Видео:213. Фокус и директриса параболы.Скачать

Составьте уравнение эллипса, фокусы которого лежат на оси ординат, E = 0, 6 и 2b = 10 ?

Составьте уравнение эллипса, фокусы которого лежат на оси ординат, E = 0, 6 и 2b = 10 .

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Составить уравнение эллипса, у которого эксцентриситет равен 0, 8, а фокальные радиусы одной из его точек равны 2 и 3?

Составить уравнение эллипса, у которого эксцентриситет равен 0, 8, а фокальные радиусы одной из его точек равны 2 и 3.

Видео:Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Составить каноническое уравнение эллипса, если известно, что расстояние между фокусом равна 6, а большая полуось — 5 единицам?

Составить каноническое уравнение эллипса, если известно, что расстояние между фокусом равна 6, а большая полуось — 5 единицам.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Построить кривую, заданную уравнением?

Построить кривую, заданную уравнением.

Найти : а) полуоси (для эллипса и гиперболы) ; б) координаты фокусов ; в) эксцентриситет (для эллипса и гиперболы) ; г) уравнения директрис.

Уравнения кривой y2(в квадрате) + 4х — 4 = 0.

Видео:11 класс, 52 урок, ЭллипсСкачать

Составить каноническое уравнение эллипса, если его большая полуось равна 12, а эксцентриситет равен 0, 8?

Составить каноническое уравнение эллипса, если его большая полуось равна 12, а эксцентриситет равен 0, 8.

Найти расстояние между фокусами эллипса.

Видео:Аналитическая геометрия: окружность и эллипсСкачать

Найти полуоси координаты фокусов и эксцентриситет и уравнение директрис эллипса 16х ^ 2 + 25y ^ 2 — 400 = 0?

Найти полуоси координаты фокусов и эксцентриситет и уравнение директрис эллипса 16х ^ 2 + 25y ^ 2 — 400 = 0.

Видео:§29 Эксцентриситет гиперболыСкачать

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы кото?

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы которого совпадают с фокусами гиперболы x ^ 2 — y ^ 2 = 8.

Видео:Видеоурок "Эллипс"Скачать

Эксцентриситет эллипса 5х ^ 2 + 9y ^ 2 = 45 равен?

Эксцентриситет эллипса 5х ^ 2 + 9y ^ 2 = 45 равен.

Вы зашли на страницу вопроса Дан эллипс 9x² + 25y² = 225 найти а) его полуоси б) фокусы в) эксцентриситет г) уравнения директрис?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

А)S = a * b S = 20 * 10 = 200 (см ^ 2) б)V = a * b * c V = 20 * 10 * 3 = 600 (см ^ 3).

Везде где нне написано что то ставь ? Знак.

40 / 2 = 20 (ш) — красных20 / 4 = 5 (ш) — желтых40 — 20 — 5 = 15 (ш) — голубых и зеленых Ответ : 15 шт.

40 / 2 = 20 красных20 / 4 = 5 желтых40 — 20 — 5 = 15 голубых и зеленых.

6. 1)0, 6 + 0, 4 = 1 2)0, 7 + 0, 5 = 1, 2 3)0, 75 — 0, 3 = 0, 45.

4x — 2x — 2 — 5 = 7x — 7 — 5x = 0 x = 0 одз х не равен 1.

Х — весь путь х — (3 / 11 * х + 2 / 11 * х) = 240 6 / 11 * х = 240 х = 440.

Сорока способами может быть получен предмет.

ДАНО p = 0. 4 — вероятность ВС n = 6 — количество проб НАЙТИ P(n.

129 * На 2, если * = 0 ; 2 ; 4 ; 6 ; 8. У вас 10 — нельзя, 10 двузначное а * это одна цифра не две. На 5, если * = 0 ; 5. На 45, если сумма цифр числа делится на 9, и вконце числа 5 или 0. Число 129 * пусть * = 0 ; 1290 = 1 + 2 + 9 + 0 = 12 сумма..

Видео:кривые второго порядка (решение задач)Скачать

Составить уравнение эллипса фокусы которого имеют координаты

Определение. Эллипс – это геометрическая фигура, которая ограничена кривой, заданной уравнением .

Он имеет два фокуса. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

Видео:Кривые второго порядка. ЗадачиСкачать

Чертеж фигуры эллипс

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси связаны соотношением:

Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r₁ + r₂ = 2*(по теореме Пифагора). В случае, если точка М находится на пересечении его с горизонтальной осью, r₁ + r ₂ = a – c + a + c. Т.к. по определению сумма r₁ + r ₂ – постоянная величина, то , приравнивая, получаем:

Эксцентриситет фигуры эллипс

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .

Если a = b ( c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х ₁ , у ₁ ) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне его.

Теорема. Для произвольной точки М(х, у), принадлежащей фигуре эллипс верны соотношения :

Доказательство. Выше было показано, что r₁ + r₂ = 2 a . Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r₂ = a + ex . Теорема доказана.

Директрисы фигуры эллипс

С фигурой эллипс связаны две прямые, называемые директрисами . Их уравнения:

x = a / e ; x = – a / e .

Теорема. Для того, чтобы точка лежала на границе фигуры эллипс, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину фигуры эллипс, заданного уравнением :

• Координаты нижней вершины: x = 0; y 2 = 16; y = -4.

• Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F₂ (-3; 0).

• Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение границы фигуры эллипс, если его фокусы F ₁ (0; 0), F₂ (1; 1), большая ось равна 2.

Уравнение границы имеет вид: . Расстояние между фокусами:

2 c = , таким образом, a 2 – b 2 = c 2 = 1/2

по условию 2а = 2, следовательно а = 1, b =

Итого искомое уравнение имеет вид: .

УСЛОВИЕ:

Составить уравнение эллипса, зная, что:
а) его большая полуось равна 10 и фокусы суть F1(-6;0), F2(10;0)
б) а=5, F1(-3;5), F2(3;5)
2.
Составить каноническое уравнение эллипса, фокусы которого расположены на оси Ох, симметрично относительно начала координат, если:
а)задана точка M1(2 корня из 3;1) эллипса и его малая полуось равна 2
б) заданы две точки эллипса M1(0;7) и M2(8;0)
в)расстояние между фокусами равно 24 и большая ось равна 26
г) экцентриситет равен 7/25 и заданы фокусы (+-7;0)

Добавил maryney23 , просмотры: ☺ 3749 ⌚ 2018-12-29 21:53:45. предмет не задан класс не задан класс

Решения пользователей

РЕШЕНИЕ ОТ sova

M- середина F_(1)F_(2)
x_(M)=(-6+10)/2=2
y_(M)=0
M(2;0)
Прямая x=2 -оcь симметрии эллипса

О т в е т.(x-2)^2/(10^2)+(y^2/6^2)=1

б) F_(1)(-3;5); F_(2)=(3;5)⇒
c=3
Прямая
y=5 – ось симметрии эллипса

О т в е т.(x^2/5^2)+((y-5)^2/4^2)=1

2. Если фокусы эллипса расположены на оси Ох, симметрично относительно начала координат, то каноническое уравнение эллипса имеет вид
(x^2/a^2)+(y^2/b^2)=1

а)
b=2
(x^2/a^2)+(y^2/4)=1
Подставляем координаты точки M_(1):
(12/a^2)+(1/4)=1
(12/a^2)=3/4
a^2=16
О т в е т. (x^2/4^2)+(y^2/2^2)=1

О т в е т. (x^2/8^2)+(y^2/7^2)=1

в)
2с=24 ⇒ с=12
2а=26 ⇒ а=13

b^2=a^2-с^2=13^2-12^2=169-144=25=5^2
О т в е т. (x^2/13^2)+(y^2/5^2)=1

г)
F( ± c;0) ⇒ c=7
ε=с/а
c/a=7/25
a=25
b^2=a^2-c^2=625-49=576=24^2
О т в е т. (x^2/25^2)+(y^2/24^2)=1

Консультации и решение задач по алгебре, геометрии, анализу, дискретной математике.

Лучшие эксперты в этом разделе

Коцюрбенко Алексей Владимирович Статус: Модератор Рейтинг: 1702

epimkin Статус: Бакалавр Рейтинг: 385

Roman Chaplinsky / Химик CH Статус: Модератор Рейтинг: 372

здравствуйте помогите пожалуйста.
Составить уравнение эллипса, фокусы которого имеют координаты (0;4√2) и (0;- 4√2) , а малая ось равна 14. спасибо за помощь

Состояние: Консультация закрыта

Здравствуйте, анисимова юлия александровна!
Уравнение эллипса имеет вид
x²/a² + y²/b² = 1 (если фокусы расположены на оси Ox)
или
x²/b² + y²/a² = 1 (если фокусы расположены на оси Oy).
У нас второй случай.

Фокусы эллипса имеют координаты (0; 4√2) и (0; -4√2), значит, c = 4√2.
Малая ось равна 14, т.е. b = 14.
У эллипса
a² = b² + c².
Значит,
a² = 196 + 32 = 228.

Ответ: x²/196 + y²/228 = 1.

Консультировал: Агапов Марсель Дата отправки: 15.01.2008, 22:17

0

Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »

Возможность оставлять сообщения в мини-форумах консультаций доступна только после входа в систему.
Воспользуйтесь кнопкой входа вверху страницы, если Вы зарегистрированы или пройдите простую процедуру регистрации на Портале.