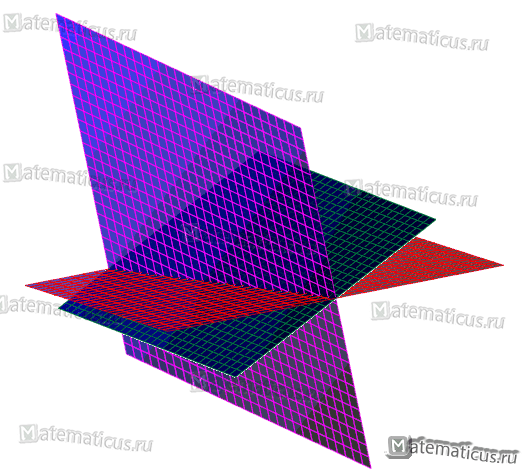
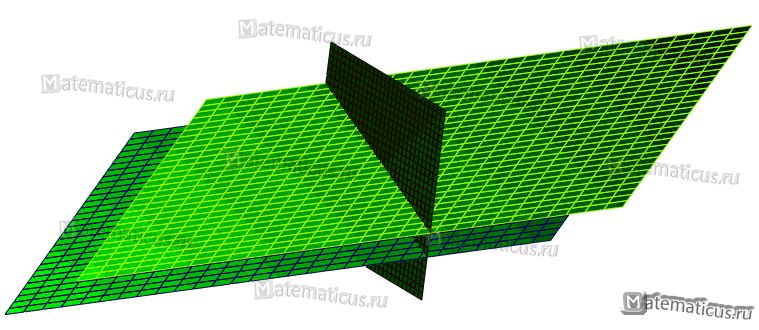
Чтобы найти координаты точки пересечения трех плоскостей, необходимо решить эти уравнения относительно х, у и z, при этом координаты точки пересечения должны удовлетворять уравнениям всех трех плоскостей.
Система уравнений трёх плоскостей имеет вид:
Если определитель этой системы не равен нулю,
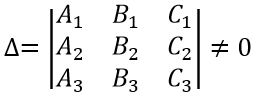
то система имеет единственное решение и тогда три плоскости пересекаются в одной точке.
1. Если три плоскости не имеют ни одной общей точки ( или хотя бы две из них параллельны) — система уравнений не имеет решений.
2.Если плоскости имеют бесчисленное множество общих точек ( все они проходят через одну прямую), то система уравнений имеет бесчисленное множество решений.
3.Если система имеет одну общую точку, то система уравнений имеет только одно решение.
Пример 1
Исследовать, есть ли общие точки у плоскостей
x+y+z=1, x-2y-3z=5, 2x-y-2z=6
Оно имеет бесчисленное множество решений. Значит, три плоскости имеют бесчисленное множество общих точек, т. е. проходят через одну прямую. 
Решая эти уравнения совместно, получим координаты искомой точки x=-1; y=1; z=2.
Таким образом плоскости имеют одну общую точку (-1; 1; 2), так как система уравнений имеет единственное решение. 
Пример 3
Плоскости
не имеют общих точек, так как плоскости (1) и (2) параллельны.
Система уравнений несовместима (уравнения (1) и (2) противоречат друг другу). 
- Взаимное расположение плоскостей: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке
- Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
- Условие пересечения трёх плоскостей в одной точке, точка пересечения
- Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости
- Точка пересечения трех плоскостей
- 📽️ Видео
Видео:23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать
Взаимное расположение плоскостей: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке
Видео:Найти точку пересечения 3х плоскостейСкачать
Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
Пусть две плоскости 
и 
заданы общими уравнениями 
и 
.
Вопрос об определении угла между ними сводится к определению угла 
между векторами нормалей к ним
и 
.
Из определения скалярного произведения 
и из выражения в координатах длин векторов 
и 
и их скалярного произведения получим
Условие параллельности плоскостей и эквивалентно условию коллинеарности векторов и и заключается в пропорциональности координат этих векторов:
.
Условие перпендикулярности плоскостей и может быть выражено равенством нулю скалярного произведения векторов нормалей к ним и :
.
Пример 1. Установить, параллельны ли две плоскости, одна из которых задана уравнением 
, а другая — уравнением 
.
Решение. Составим уравнения коэффициентов уравнений плоскостей:
Так как 
, то коэффициенты пропорциональны, следовательно данные две плоскости параллельны.
Пример 2. Установить, перпендикулярны ли плоскости, заданные уравнениями 
и 
.
Решение. Плоскости перпендикулярны в том случае, когда векторы 
и 
нормалей к ним перпендикулярны и удовлетворяют условию равенства нулю их скалярного произведения. Так как 
, то указанное условие выполнено и, значит, данные плоскости перпендикулярны.
Видео:Найти точку пересечения прямой и плоскостиСкачать
Условие пересечения трёх плоскостей в одной точке, точка пересечения
Необходимым и достаточным условием того, что три плоскости имеют только одну общую точку (то есть, пересекаются в этой точке), является условие неравенства нулю определителя, составленного из коэффициентов уравнений:
Это условие совпадает с условием того, что система линейных уравнений имеет одно единственное решение (пройдя по ссылке можно увидеть иллюстрацию как раз на примере плоскостей).
Решение системы общих уравнений плоскостей (если оно существует и единственное) и даёт точку пересечения трёх плоскостей.
Пример 3. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:
Решение. Сначала проверим, выполняется ли условие пересечения плоскостей в одной точке. Для этого установим, отличен ли от нуля определитель системы:
Определитель отличен от нуля, следовательно система уравнений имеет единственное решение, а, значит, три плоскости пересекаются в одной точке.
Для нахождения этой точки продолжим решать систему уравнений методом Крамера. Перенесём свободные члены в правые части уравнений:
Найдём определители при неизвестных:
Нетрудно заметить, что по формулам Крамера (определитель при неизвестной делить на определитель системы) все неизвестные оказались равными единице. Таким образом, получили точку пересечения трёх плоскостей:
Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.
Пример 4. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:
Решение. Проверим, пересекаются ли плоскости в одной точке. Для этого вычислим определитель системы:
Определитель равен нулю, следовательно, данные три плоскости не пересекаются в одной точке.
Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.
Видео:Уравнение плоскости через 3 точкиСкачать
Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости
Пусть даны точка 
и плоскость 
. Тогда уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости, имеет вид
.
Пример 5. Составить уравнение плоскости, проходящей через точку (3, -5, 1) , и параллельной плоскости 
.
Решение. Подставляем в формулу, данную в теоретической сравке к этой главе, данные точки и другой плоскости. Получаем:
Последнее и есть искомое уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости.
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать
Точка пересечения трех плоскостей
| Исходная система уравнений |
| Фундаментальное решение системы уравнений |
Определяем точку пересечения трех плоскостей, как решение системы из трех уравнений
Уравнения плоскостей заданы в виде
Решая эту систему уравнений, мы получаем однозначный результат
Введя данные мы получим
| Исходная система уравнений |
| Фундаментальная система решений (ФСР) данной системы уравнений |
| База системы/знаменатель |
