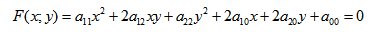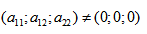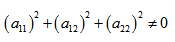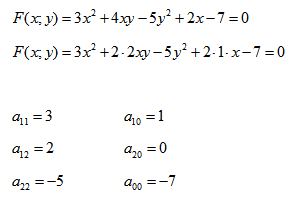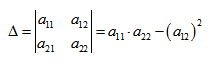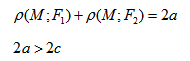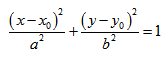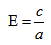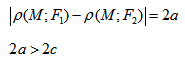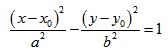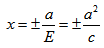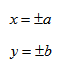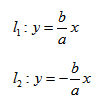Услуги токарных работ metallnk.ru. . Детальное описание Лестницы Уфа на нашем сайте.
- Аналитическая геометрия
- Теория: 11 Пересечение прямой с гиперболой/параболой (в стадии наполнения)
- Кривые второго порядка
- Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
- Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
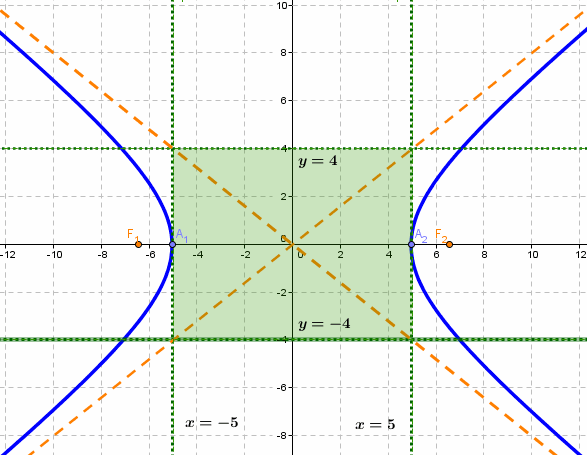
- Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
- Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
- 📺 Видео
Видео:Гипербола. Точка пересечения с графиком прямой пропорциональности.Скачать

Аналитическая геометрия
Гипербола
Каноническое уравнение гиперболы

Обозначим фокусы через 

расстояние между ними через 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2а. По определению 2а
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Теория: 11 Пересечение прямой с гиперболой/параболой (в стадии наполнения)
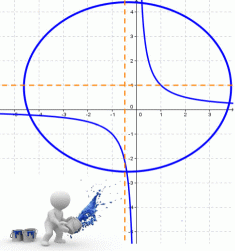
На рисунке изображены графики функций (displaystyle fleft(xright)=dfrac) и (displaystyle gleft(xright)=dfracx+1) которые пересекаются в точках (displaystyle A) и (displaystyle B) Найдите ординату точки (displaystyle B)
По условию задачи, графики функций (displaystyle fleft(xright)=frac) и (displaystyle gleft(xright)=fracx+1) пересекаются
в точках (displaystyle A) и (displaystyle B)
Точку (displaystyle A) видно на рисунке, а точку (displaystyle B) – нет.
Точки (displaystyle A) и (displaystyle B) – это точки пересечения графиков функций (displaystyle fleft(xright)=frac) и (displaystyle gleft(xright)=fracx+1)
Значит, координаты этих точек удовлетворяют и уравнению гиперболы, и уравнению прямой:
Так как (displaystyle y=frac ) и (displaystyle y=fracx+1 ) то
Решим полученное уравнение.
Перенесем все в левую часть и приведем к общему знаменателю.
Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю.
Решим квадратное уравнение (displaystyle x^2+2x-8=0)
Решим квадратное уравнение (displaystyle x^2+2x-8=0)
Найдем корни уравнения:
Значит, (displaystyle x_1=-4) и (displaystyle x_2=2) – корни квадратного уравнения (displaystyle x^2+2x-8=0)
Оба корня (displaystyle x_1=-4) и (displaystyle x_2=2) удовлетворяют ограничению (displaystyle x,cancel,0 ) Значит, они являются корнями исходного уравнения.
Таким образом, абсциссы точек пересечения графиков функций (displaystyle fleft(xright)=frac) и (displaystyle gleft(xright)=fracx+1) равны
(displaystyle x_1=-4) и (displaystyle x_2=2)
Значения (displaystyle x_1=-4) и (displaystyle x_2=2) соответствуют двум точкам пересечения (displaystyle A ) и (displaystyle B )
Точка (displaystyle B) которой не видно на рисунке, расположена левее точки (displaystyle A)
Значит, абсцисса точки (displaystyle B) меньше, чем абсцисса точки (displaystyle A)
Поэтому точке (displaystyle B) соответствует (displaystyle x_1=-4)
Найдем ординату точки (displaystyle B) подставив найденное значение (displaystyle x=-4) в уравнение (displaystyle fleft(xright)=frac) или (displaystyle gleft(xright)=fracx+1)
Воспользуемся уравнением гиперболы (displaystyle fleft(xright)=dfrac)
Значит, (displaystyle y=-1) – ордината точки (displaystyle B)
Видео:Пересечение гиперболы и прямойСкачать

Кривые второго порядка
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Видео:Видеоурок "Гипербола"Скачать

Видео:Найти точку пересечения прямой и плоскостиСкачать

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

или можно встретить следующую форму записи:
Видео:Найти абсциссу второй точки пересечения параболы и прямойСкачать

К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
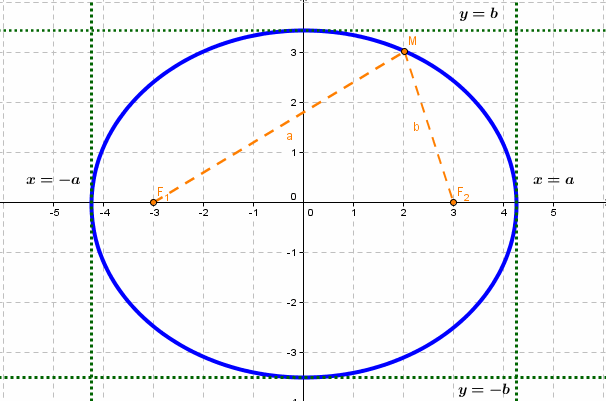
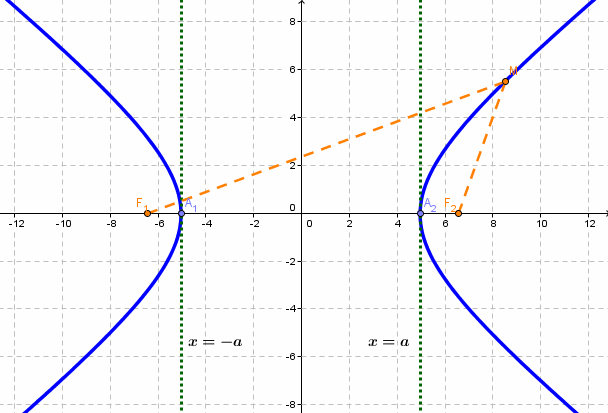
если Δ F1 и F2 — фокусы.
 |
 |
 | 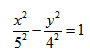 |
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
📺 Видео
Как распознать талантливого математикаСкачать

Задание 22 ОГЭ. Найти точку пересечения прямой и параболы// Построить графики в одной системеСкачать

Нахождение координат точек пересечения графика функции с осями координатСкачать

Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Как построить график функции без таблицыСкачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать