Онлайн калькулятор рассчитывает тангенциальное ускорение точки или время движения по формулам.
Формула тангенциального ускорения точки a = (v1-v0) / t, из конечной скорости вычитаем начальную и делим на время.
Формула времени движения точки t = (v1-v0) / a, из конечной скорости вычитаем начальную и делим на ускорение.
- Онлайн калькулятор тангенциального ускорения точки или время движения
- Посчитать тангенциальное ускорение, скорость или время
- Другие онлайн калькуляторы
- Теоретический материал
- Рассчитайте цену решения ваших задач
- Калькулятор стоимости
- Решение контрольной 300-600 рублей —> от 300 рублей *
- Тангенциальное ускорение — определение, формула и измерение
- Общие сведения
- Угловое ускорение
- Вывод формулы
- Решение простых примеров
- Сложная задача
- 📺 Видео
Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Онлайн калькулятор тангенциального ускорения точки или время движения
При использовании не целых чисел — ставьте точку, а не запятую.
| Рассчитываем |
| Ускорение (a) | м/с 2 |
| Время движения (t) | сек |
| Начальная скорость (V0) | м/с |
| Конечная скорость (V1) | м/с |
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Видео:Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать
Посчитать тангенциальное ускорение, скорость или время
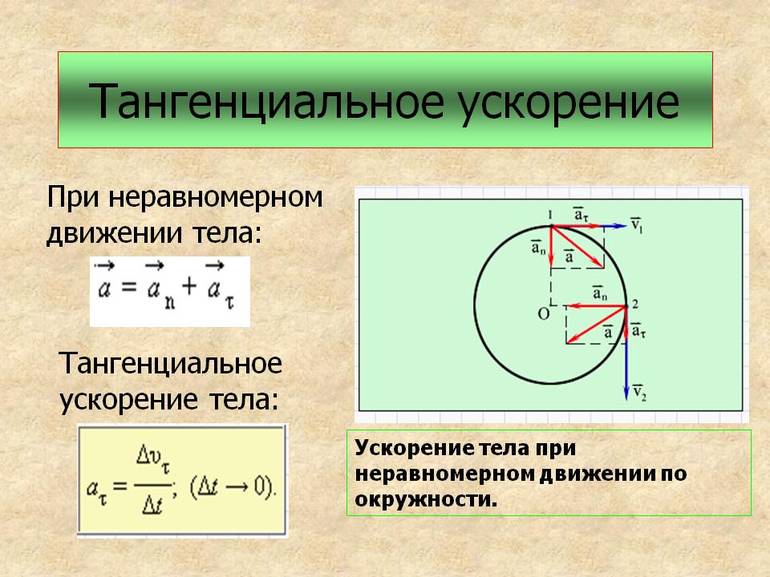
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения, характеризующая изменение модуля скорости.
Формула тангенциального ускорения
где V0, V1 — начальная и конечная скорость, t — время движения
Решили сегодня: раз, всего раз
Другие онлайн калькуляторы
Вы поняли, как решать? Нет?
Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Теоретический материал
Рассчитайте цену решения ваших задач
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Калькулятор
стоимости
Решение контрольной
300-600 рублей —> от 300 рублей *
* Точная стоимость будет определена после загрузки задания для исполнителя
Копирование материалов с сайта возможно только с разрешения администрации портала и при наличие активной ссылки на источник.
«Сегодня от своего лица хочу поблагодарить этот сайт за помощь мне с учебой. Здесь я пользовалась не только материалами, но и нашла преподавателей которые решали мне задачи.
Если тебе нужно что-то сделать в универе, я сама рекомендую. А также пользуйся моей ссылкой и получай 300 руб. на счёт при регистрации.»
Видео:Естественный способ задания движенияСкачать

Тангенциальное ускорение — определение, формула и измерение
Видео:Кинематика точки Задание К1Скачать

Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
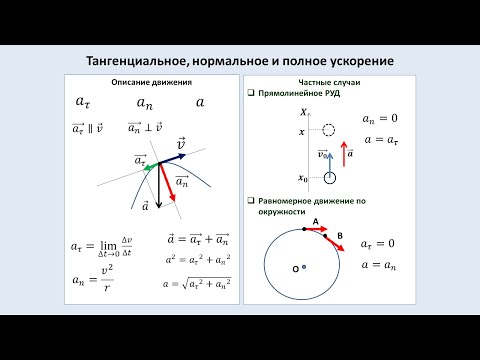
- Тангенциальное — направленное вдоль касательного пути точки в определённый момент. Из-за происхождения слова его часто называют касательным.
- Нормальное — совпадающее с нормалью траектории изменения положения.
- Полное — определяющееся суммой тангенциального и нормального ускорений.
Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

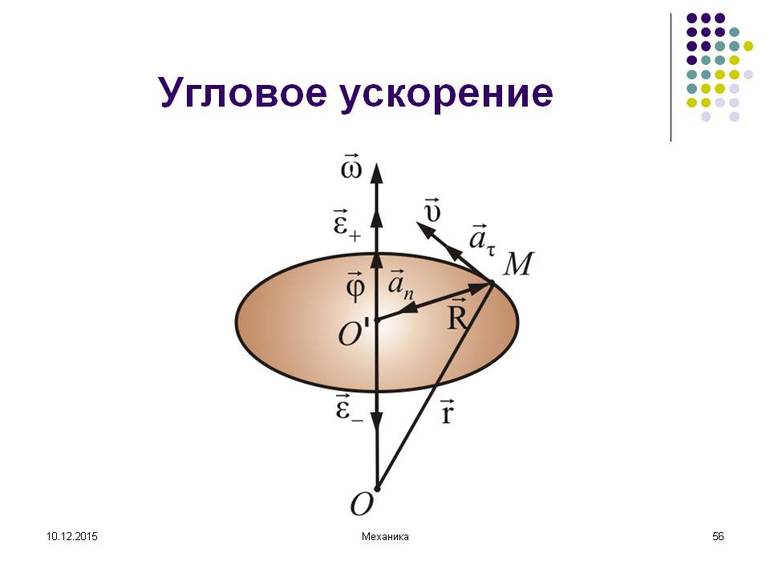
Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Видео:Скорость и ускорение точки в полярных координатахСкачать

Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
- Через промежуток времени Δt скорость изменяется как по направлению, так и по модулю: Δt = t — t0.
- Вектор изменения скорости, определяемый по правилу треугольника, будет равняться разности существующей скорости на данный момент и начальной: Δv = v — v0.
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
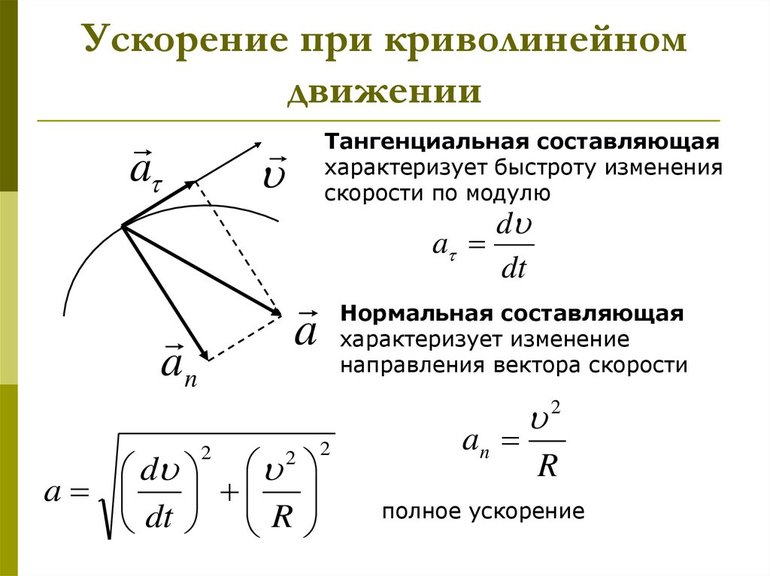
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
- at — тангенциальной составляющей, совпадающей с отрезком V;
- an — перпендикулярным по отношению расположения V вектором.
Используя теорему Пифагора, можно сказать, что модуль полного ускорения равняется корню квадратному из суммы квадратов тангенциального и нормального ускорения: a = √at 2 + an 2 .
Видео:кинематика точкиСкачать

Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
- Вычислить все ускорения точки, лежащей на окружности, через десять секунд после воздействия на диск вращателя. При этом учесть, что радиус окружности составит 20 см, а угол между валом и радиус вектором тела соответствует закону: j =3-t+0.2t 3 . Для решения примера необходимо использовать формулы для нахождения угловой скорости и ускорения. Подставив заданные значения, можно получить: w = d φ / dt = -1 + 0,2 * 3t 2 и e = dw / dt = 0,6 * 2t. Применив формулу связи, легко найти ускорение: at = R * E * (0,6 * 2t) = 1,2 * Rt = 24 м 2 /с. Подставив в формулу нормального ускорения значения, можно вычислить и его an = V 2 / R = R * (0,6 * 10 2 — 1) 2 / 0,2 = 696 м/с 2 . Отсюда полное ускорение будет равняться: a = √ 24 2 + 696 2 = 697 м/с 2 .
- Материальное тело перемещается по окружности, имеющей радиус 20 см. При этом тангенциальное ускорение равняется 5 см на секунду в квадрате. Определить, сколько понадобится времени, чтобы ускорения сравнялись и нормальное стало больше тангенциального в два раза. Исходя из условия, можно утверждать, что движение является равноускоренным. Поэтому можно применить формулы: an = V2 / t; at = V / t. Отсюда: t = V / at, а V = √an * R. Подставив второе выражение в первое, получится: t = (√an * R) / at. При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Видео:Камень брошен горизонтально, надо искать радиус кривизны траектории. (Волькенштейн 1.20)Скачать

Сложная задача
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Нормальное ускорение можно выразить через скорость и радиус: an = V 2 / R. Затем необходимо записать формулу для тангенциального ускорения: at = dV / dt. Так как они равны, то справедливым будет равенство: V 2 / R = dV / dt. Анализируя уравнение, можно сделать вывод, что так как скорость и радиус положительный, то слева будет стоять величина со знаком плюс. Но, с другой стороны, со временем скорость убывает, поэтому с правой стороны нужно поставить знак минус: V 2 / R = — dV / dt.
Полученное уравнение является дифференциальным и показывает зависимость скорости от времени. Равенство можно преобразовать, умножив на отношение dt / V 2 . В итоге должно получиться выражение: dV / V 2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Теперь можно найти тангенциальное убыстрение, так как оно представляет производную от скорости. После взятия производной получится: at = dV / dt = — V02 / R (1 + V0 * t / R)2 = — V2 / R. Отсюда можно написать, что модуль полного ускорения будет равняться: a = √2 *|ar| = (√2 * V2) / R. Осталось найти путь. Он совпадает с длиной дуг и равняется интегралу модуля скорости от времени. После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.
📺 Видео
Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

Нормальное и тангенциальное ускорение [Физзадачи #37]Скачать
![Нормальное и тангенциальное ускорение [Физзадачи #37]](https://i.ytimg.com/vi/HTVGtCaQgEk/0.jpg)
Теоретическая механика. Задание К1 (часть 1) из сборника ЯблонскогоСкачать

Определение абсолютной скорости и абсолютного ускорения точкиСкачать
7.8. Ускорение точки при естественном способе задания движенияСкачать

Нормальное и тангенциальное ускорениеСкачать

КАК найти зависимость СКОРОСТИ и УСКОРЕНИЯ от КООРДИНАТЫ или УГЛА в задачах на КИНЕМАТИЧЕСКИЕ СВЯЗИСкачать

Движение тела, брошенного под углом к горизонтуСкачать

Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Cложное движение точки. ТермехСкачать