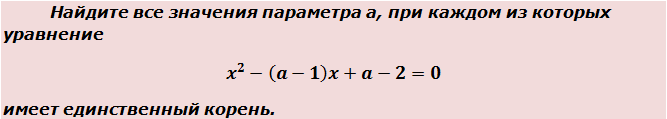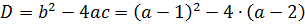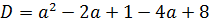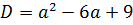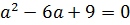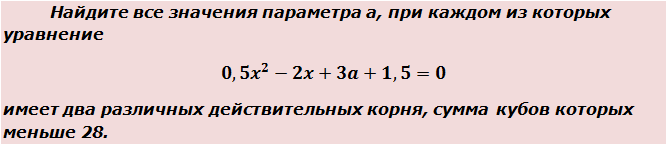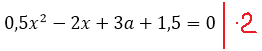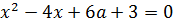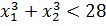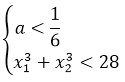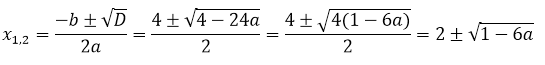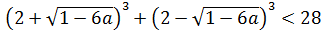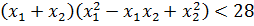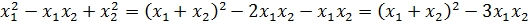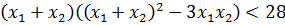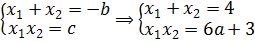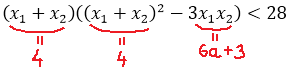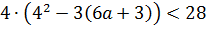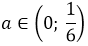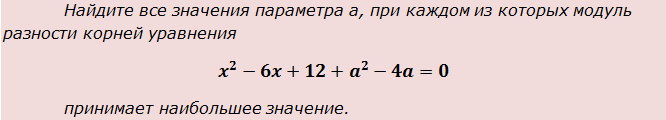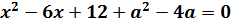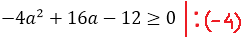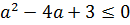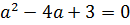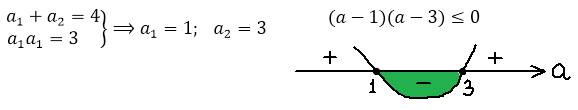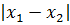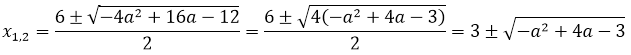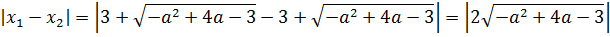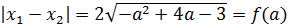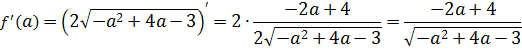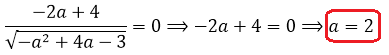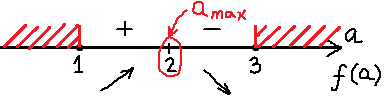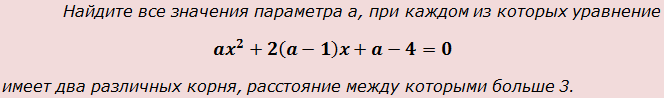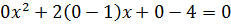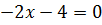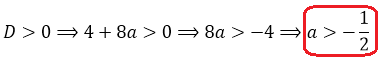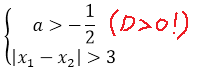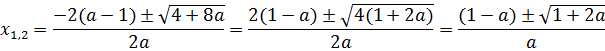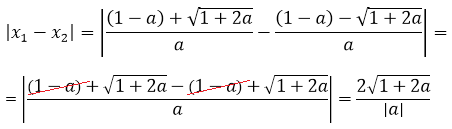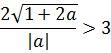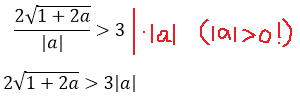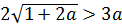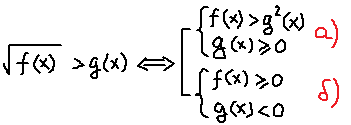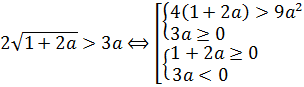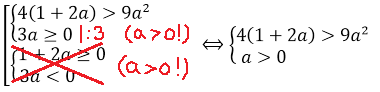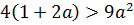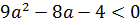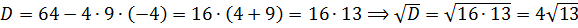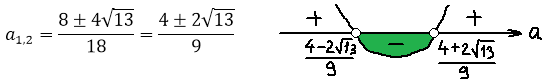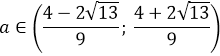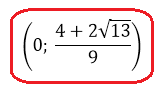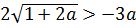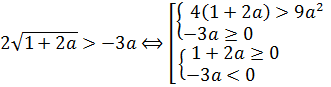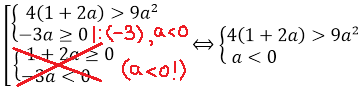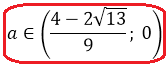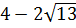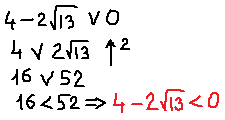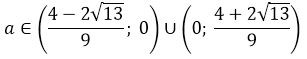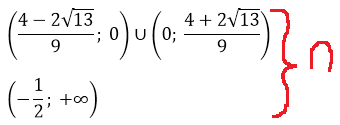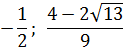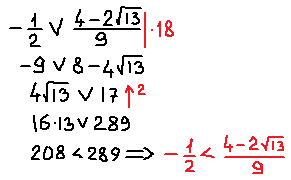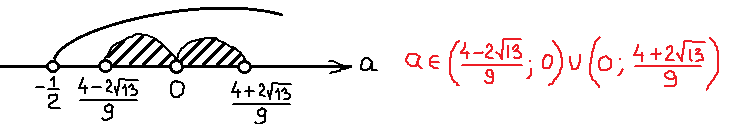Найти сумму значений параметра для которых уравнение будет иметь три корня

Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.

Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!

Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:

— Что такое квадратное уравнение, как оно выглядит и как решается?

— Что такое дискриминант и куда его пристроить?

— Что такое теорема Виета и где её можно применить?

Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.

Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂

Пример 1

Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:

Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.

Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!

Теперь надо приравнять наш дискриминант к нулю:

Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3) 2 !

Респект внимательным! Верно! Если заменить наше выражение слева на (a-3) 2 , то уравнение будет решаться в уме!

Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)

Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.

Пример 2

Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:

0,5x 2 — 2x + 3a + 1,5 = 0

Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:

Выписываем в столбик наши коэффициенты a, b, c:

Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!

А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:

«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»

Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:

Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.

Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:

Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:

А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.

Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:

Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:

А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.

Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:

А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:

Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:

Чему здесь равен коэффициент при x 2 ? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:

Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:

Осталось раскрыть скобки и решить простенькое линейное неравенство:

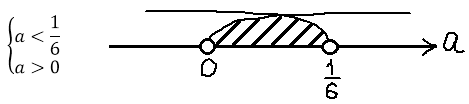
Вспоминаем, что ещё у нас есть глобальное требование a 0 необходимо пересечь с условием a . Рисуем картинку, пересекаем, и записываем окончательный ответ.

Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!

Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.

Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.

Например, такая задачка из реального варианта ЕГЭ:

Пример 3

Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»

Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:

А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:

Что ж, аккуратно расписываем наш дискриминант через параметр а:

А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:

Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)

А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука

принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x₁ — x₂. Теорема Виета здесь в этот раз бессильна.

Что ж, считаем корни по общей формуле:

Дальше составляем модуль разности этих самых корней:

Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:

И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)

Дифференцируем нашу функцию и приравниваем производную к нулю:

Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).

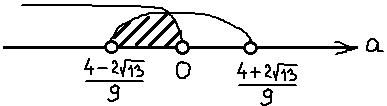
Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.

Всё. Вот теперь наша задача полностью решена.

Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).

Пример 4

Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?

Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)

При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.

А далее по накатанной колее. Считаем дискриминант:

D = 4(a-1) 2 — 4a(a-4) = 4a 2 -8a+4-4a 2 +16a = 4+8a

Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.

Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:

Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.

Значит, ответом на вопрос задачи является решение вот такой системы:

Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:

Отлично. Корни получены. Теперь начинаем формировать наше расстояние:

Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:

Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.

Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:

Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.

Случай 1 (a>0, |a|=a)

В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:

Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:

Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.

Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:

А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a 0 и a

Упрощаем нашу совокупность с учётом главного условия a>0:

Вот так. А теперь решаем самое обычное квадратное неравенство:

Нас интересует промежуток между корнями. Стало быть,

Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:

Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:

Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.

Случай 2 (a

В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:

Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):

С учётом общего требования a

А дальше снова решаем обычное квадратное неравенство:

И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:

Осталось лишь пересечь этот интервал с нашим новым условием a

Вот и второй кусочек ответа готов:

Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число

с нулём. Вот так:

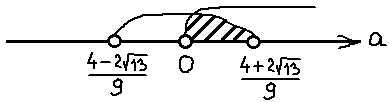
А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):

Готово дело. Эти два интервала — это пока ещё только решение неравенства

Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!

Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:

Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:

Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:

Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая:

Всё, задача полностью решена и можно записывать окончательный ответ.

Ну как? Уловили суть? Тогда решаем самостоятельно.)

1. Найдите все значения параметра b, при которых уравнение

ax 2 + 3x +5 = 0

имеет единственный корень.

2. Найдите все значения параметра а, при каждом из которых больший корень уравнения

x 2 — (14a-9)x + 49a 2 — 63a + 20 = 0

3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения

x 2 — 4ax + 5a = 0

4. Найдите все значения параметра а, при каждом из которых уравнение

x 2 + 2(a-2)x + a + 3 = 0

имеет два различных корня, расстояние между которыми больше 3.

Видео:Найдите все значения параметра m≦100 , при которых уравнение σ(x)=m имеет решениеСкачать

Задача 18 ЕГЭ-2021 по математике. Параметры

Посмотрите на условия задач с параметрами ЕГЭ-2021. Вы заметите, что на вид все они похожи. Однако сходство только внешнее, и решаются они по-разному. В этой статье – обзор задач с параметрами ЕГЭ-2021 по математике.

1. Начнем с задачи, которую лучше всего решить аналитическим способом. Слева в уравнении модуль, справа – произведение модуля и корня квадратного. Лучше всего первым действием сделать возведение обеих частей уравнения в квадрат (при неотрицательности подкоренного выражения).

О том, как решать уравнения, где слева модуль и справа модуль, читайте здесь: Уравнения с модулем.

При каких значениях параметра a уравнение

имеет ровно 2 решения?

Уравнение равносильно системе:

Вынесли общий множитель за скобку

Так как и при всех исходное уравнение имеет корни и при всех Значит, исходное уравнение имеет ровно два корня в следующих случаях:

не имеет решений и

2) совпадение корней

Рассмотрим первый случай.

Неравенство — не имеет решений, если

Рассмотрим второй случай.

1) Корни и совпадают, тогда и

Так как исходное уравнение при имеет один корень

2) Корни и совпадают.

Уравнение имеет корни и

3) Корни и совпадают, исходное уравнение имеет ровно два корня.

Мы применили аналитический способ решения: с помощью равносильных переходов от исходного уравнения перешли к такой форме, где сразу видно, какие корни имеет уравнение при определенных значениях параметра.

На Онлайн-курсе подготовки к ЕГЭ на 100 баллов мы подробно рассказывали об этом методе и решали множество задач. Способ хорош тем, что вы просто действуете по образцу – и быстро приходите к ответу.

2. Второе уравнение очень похоже на первое. И первое действие будет таким же: возведением обеих частей в квадрат. А закончим мы – для разнообразия – построением графиков в системе координат (а; х).

Найти a, при которых имеет ровно 2 решения.

Возведем обе части уравнения в квадрат.

Найдем, каким значениям параметра соответствует ровно два значения

Построим в системе координат графики функций:

Мы находим такие при которых горизонтальная прямая имеет ровно 2 общие точки с совокупностью прямых, являющихся графиком исходного уравнения.

Видим, что в общем случае прямая пересекает каждую из трех прямых, то есть исходное уравнение имеет ровно 3 решения.
Ровно 2 решения будет в случаях, когда прямая проходит через точки пересечения прямых, то есть в случаях совпадения корней.

Данная совокупность имеет ровно два решения в случаях совпадения корней.

О графическом способе решения задач с параметрами читайте здесь: Графический метод решения задач с параметрами.

3. В третьем задании также присутствуют выражения под модулями. Но подход будет другой: мы применим метод интервалов для модулей, о котором можно прочитать здесь: Уравнения с модулем.

С его помощью раскроем модули и получим график функции, заданной описанием: на разных интервалах график этой функции выглядит по-разному, то есть состоит из отдельных кусочков. А дальше – графическое решение.

Найдите все значения a, при каждом из которых уравнение

имеет ровно два различных корня.

Применим метод интервалов для модулей. Уравнение равносильно совокупности систем:

Мы сделали так, потому что при оба модуля раскрываем с противоположным знаком:

Заметим, что если уравнение не выполняется ни при каких

Решим графически полученную совокупность.

Рассмотрим функцию такую, что:

Для функции ось ординат – вертикальная асимптота.

Уравнение имеет ровно два корня при или

Вообще задачи с параметрами, как правило, можно решать многими способами.

4. И наконец, довольно сложное уравнение с тремя модулями. Нам придется раскрывать все эти модули по определению, рассматривая 4 случая. Но ничего страшного здесь нет – просто аккуратность. А потом мы разобьем координатную плоскость (х; а) на области и в каждой из областей построим график уравнения. Кто знаком с методом областей – тот легко с этим справится.

При каких значениях параметра a уравнение имеет ровно три различных решения

2) Пусть тогда Получим:

Изобразим полученную совокупность условий в координатах

Получим области I — IV, соответствующие

Получили график уравнения.

Уравнение имеет ровно 3 решения, если значение a соответствует одной из точек пересечения прямых: точка A, B, С или D. В остальных случаях уравнение имеет ровно 4 решения.

5. (Резервный день) Найти все значения параметра при каждом из которых уравнение

имеет хотя бы два различных корня.

Исходное уравнение имеет хотя бы два различных корня, если уравнение

имеет хотя бы один корень

Если t = 0, то x = 0, тогда

Этот случай рассмотрим отдельно.

1) Случай уравнение

должно иметь хотя бы один положительный корень.

Если уравнение линейное, тогда

Пусть уравнение квадратное.

При этом должно выполняться условие

Решим третье неравенство системы:

возведем обе части в квадрат:

Объединив со случаем a = 2, получим:

Вернемся к случаю, когда – корень уравнения. Тогда Получим уравнение:

– уравнение имеет, кроме корня положительный корень подходит

Вот так в задачах ЕГЭ-2021 по математике можно применить в задачах с параметрами аналитический и графический способы, а также метод областей.

Конечно, это не все. Существует не менее 12 методов решения задач с параметрами. Мы изучаем их все на практике на Онлайн-курсе подготовки к ЕГЭ по математике.

Видео:Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Урок по теме «Методы решения задач с параметрами»

Разделы: Математика

Цель данной работы – изучение различных способов решения задач с параметрами. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы длительнее усилия, именно поэтому в профильных 10-11 классах с углубленным изучением точных наук введен курс: “Математический практикум”, частью которого является решение уравнений и неравенств с параметрами. Курс входит в число дисциплин, включенных в компонент учебного плана школы.

Успешному изучению методов решения задач с параметрами могут помочь элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с параметрами”.

Рассмотрим четыре больших класса задач с параметрами:

1. Уравнения, неравенства и их системы, которые необходимо решить для любого значения параметра, либо для значений параметра, принадлежащих определенному множеству.
2. Уравнения, неравенства и их системы, для которых требуется определить количество решений в зависимости от значения параметра.
3. Уравнения, неравенства и их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения (системы, неравенства) имеют заданное число решений.
4. Уравнения, неравенства и их системы, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Методы решений задач с параметрами.

1. Аналитический метод.

Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Пример 1. Найдите все значения параметра a, при которых уравнение:

(2a – 1)x 2 + ax + (2a – 3) =0 имеет не более одного корня.

При 2a – 1 = 0 данное уравнение квадратным не является, поэтому случай a =1/2 разбираем отдельно.

Если a = 1/2, то уравнение принимает вид 1/2x – 2 = 0, оно имеет один корень.

Если a ≠ 1/2 , то уравнение является квадратным; чтобы оно имело не более одного корня необходимо и достаточно, чтобы дискриминант был неположителен:

Чтобы записать окончательный ответ, необходимо понять,

2. Графический метод.

В зависимости от задачи (с переменной x и параметром a) рассматриваются графики в координатной плоскости (x;y) или в плоскости (x;a).

Пример 2. Для каждого значения параметра a определите количество решений уравнения .

Заметим, что количество решений уравнения равно количеству точек пересечения графиков функций и y = a.

График функции показан на рис.1.

y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).

Ответ: при a 25/4 – два решения.

3. Метод решения относительно параметра.

При решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

Пример 3. Найти все значения параметра а , при каждом из которых уравнение = —ax +3a +2 имеет единственное решение.

Будем решать это уравнение заменой переменных. Пусть = t , t ≥ 0 , тогда x = t 2 + 8 и уравнение примет вид at 2 + t + 5a – 2 = 0 . Теперь задача состоит в том, чтобы найти все а, при которых уравнение at 2 + t + 5a – 2 = 0 имеет единственное неотрицательное решение. Это имеет место в следующих случаях.

1) Если а = 0, то уравнение имеет единственное решение t = 2.

Решение некоторых типов уравнений и неравенств с параметрами.

Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности.

Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.

Задача № 1. При каких значениях параметра b уравнение не имеет корней?

Ⅱ . Степенные уравнения, неравенства и их системы.

Задача №2. Найти все значения параметра a, при которых множество решений неравенства:

содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.

.

Преобразуем обе части неравенства.

Для того, чтобы множество решений неравенства содержало число 6, необходимо и достаточно выполнение условия:

Рис.4

При a > 6 множество решений неравенства: .

Интервал (0;5) не может содержать ни одного отрезка длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в интервале (5; a).

Это

Ⅲ . Показательные уравнения, неравенства и системы.

Задача № 3. В области определения функции взяли все целые положительные числа и сложили их. Найти все значения, при которых такая сумма будет больше 5, но меньше 10.

1) Графиком дробно-линейной функции является гипербола. По условию x > 0. При неограниченном возрастании х дробь монотонно убывает и приближается к нулю, а значения функции z возрастают и приближаются к 5. Кроме того, z(0) = 1.

2) По определению степени область определения D(y) состоит из решений неравенства . При a = 1 получаем неравенство, у которого решений нет. Поэтому функция у нигде не определена.

3) При 0 0 , то z(x) > z(0) = 1 . Значит, каждое положительное значение х является решением неравенства . Поэтому для таких а указанную в условии сумму нельзя найти.

4) При a > 1 показательная функция с основанием а возрастает и неравенство равносильно неравенству . Если a ≥ 5 , то любое положительное число является его решением, и указанную в условии сумму нельзя найти. Если 1 . Так как возрастает на , то z(3) .

Решение иррациональных уравнений и неравенств, а также уравнений, неравенств и систем, содержащих модули рассмотрены в Приложении 1.

Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.

По статистике многие из выпускников не приступают к решению задач с параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Репетитор по математике

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Видео:#67. Сумма квадратов корней в уравнении с параметром!Скачать

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Видео:#118 Урок 43 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Скачать

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

🎥 Видео

Хороший ПАРАМЕТР ★ Задание 18 ЕГЭ профиль #56Скачать

При каких значениях параметра уравнение имеет единственный кореньСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Найдите все значения а, при каждом из которых уравнение 64x^6+4x^2=(3x+a)^3+3x+a не имеет корней.Скачать

Уравнения с параметром. Алгебра, 8 классСкачать

Найдите все значения параметра a, при каждом из которых уравнение имеет ровно два различных корняСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive​​ #041 | Борис ТрушинСкачать

Найти значение суммы и произведения корней квадратного уравненияСкачать

ЕГЭ по математике, c5. Уравнение с параметромСкачать

6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать

Задача с параметром 18 ЕГЭ профиль #46Скачать

РАЗБОР СЛОЖНОГО ЗАДАНИЯ 18, ПАРАМЕТР. ЕГЭ МАТЕМАТИКА с Артуром ШарифовымСкачать

Квадратное уравнение с параметром. Исследование корней квадратного уравнения. Алгебра 8 классСкачать

Задание С5. Показательное уравнение с параметром - bezbotvyСкачать

Задача с параметром по математике из дополнительного вступительного испытания в МГУСкачать