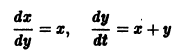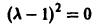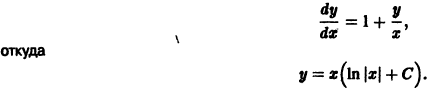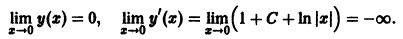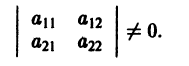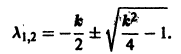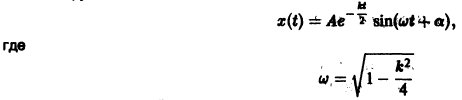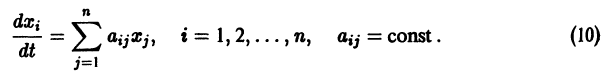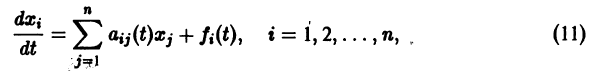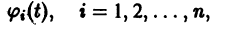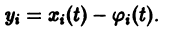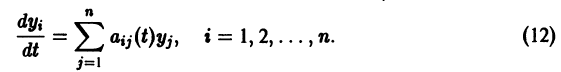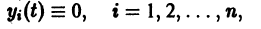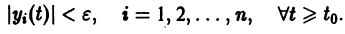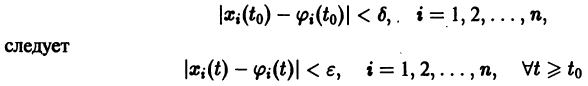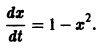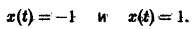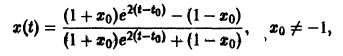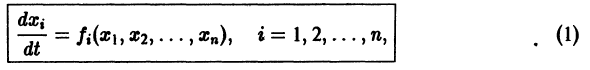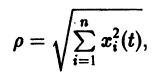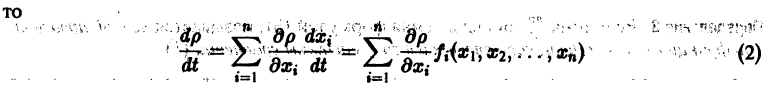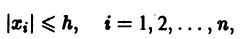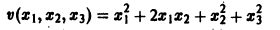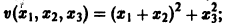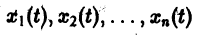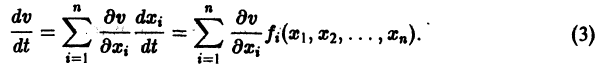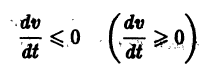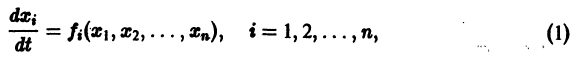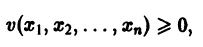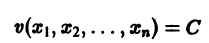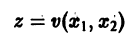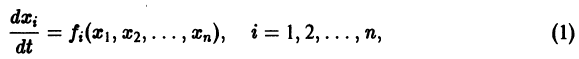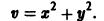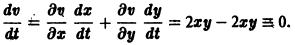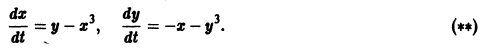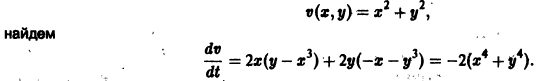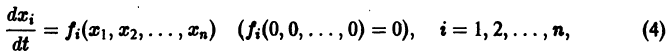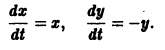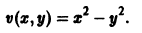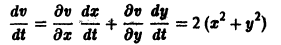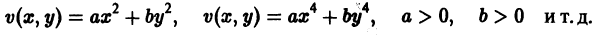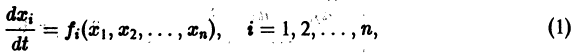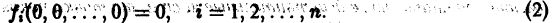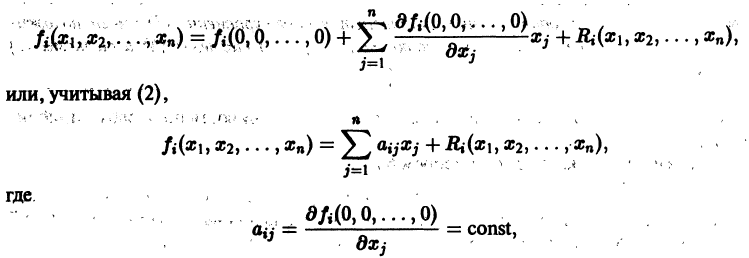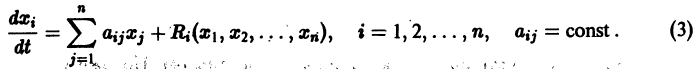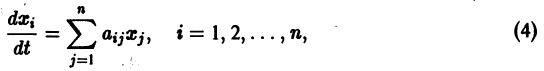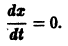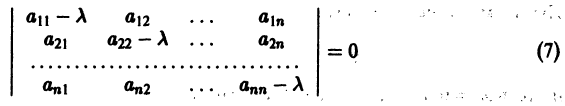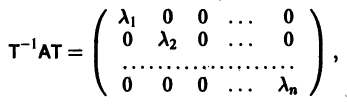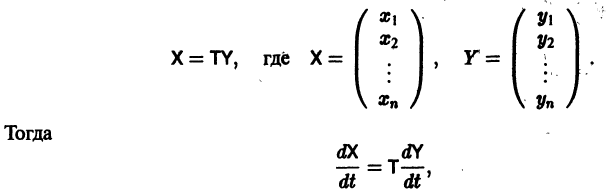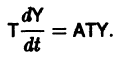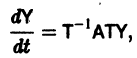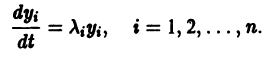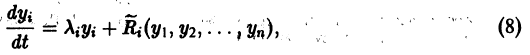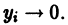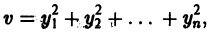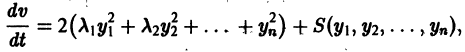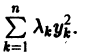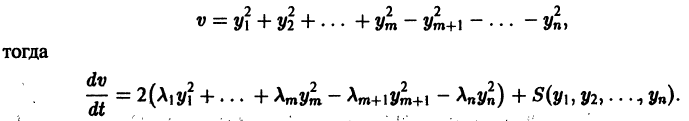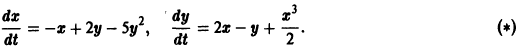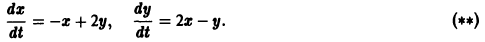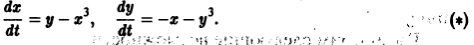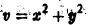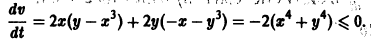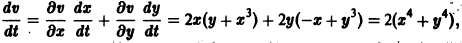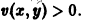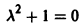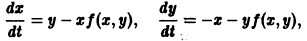МОДЕЛИ БИОЛОГИЧЕСКИХ СИСТЕМ, ОПИСЫВАЕМЫЕ
ОДНИМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ ПЕРВОГО ПОРЯДКА
Модели, приводящие к одному дифференциальному уравнению. Понятие решения одного автономного дифференциального уравнения. Стационарное состояние (состояние равновесия). Устойчивость состояния равновесия. Методы оценки устойчивости. Решение линейного дифференциального уравнения Примеры: экспоненциальный рост, логистический рост.
Изучение математических моделей биологических систем начнем с систем первого порядка, которым соответствует одно дифференциальное уравнение первого порядка:
Если система автономная, то правая часть уравнений не зависит явно от времени и уравнение имеет вид:
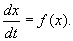
Состояние таких систем в каждый момент времени характеризуется одной единственной величиной – значением переменной x в данный момент времени t.
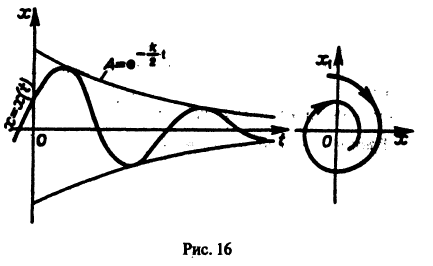
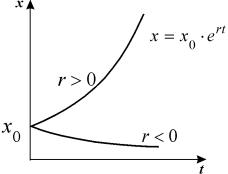
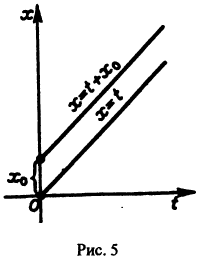
Рассмотрим плоскость t, x. Решениями уравнения (2.1): x( t) являются кривые на плоскости t, x , называемые интегральными кривыми (рис. 2.1)
Пусть заданы начальные условия 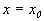
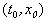
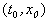
Рис. 2.1. Интегральные кривые x ( t ); – решения уравнения f ( x ) = 0

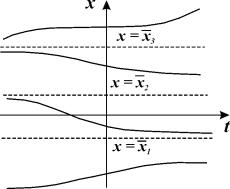
Интегральные кривые уравнения (2.1) не могут пересекаться. Решения уравнения (2.1) не могут быть периодическими, они монотонны.
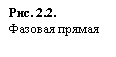
Поведение интегральных кривых на плоскости t, x можно установить, не решая в явном виде дифференциального уравнения (2.1), если известен характер движения изображающей точки на фазовой прямой.
Рассмотрим плоскость t, x , причем фазовую прямую совместим с осью x . Построим на плоскости t, x точку с абсциссой t и с ординатой, равной смещению изображающей точки по оси x в данный момент времени t. С течением времени в соответствии с уравнением (2.1) изображающая точка будет двигаться по фазовой прямой (рис. 2.2), а на плоскости t, x описывать некую кривую. Это будет интегральная кривая уравнения (2.1).
Решения одного автономного дифференциального уравнения либо уходят в бесконечность (чего не бывает в реальных системах), либо асимптотически приближаются к стационарному состоянию.
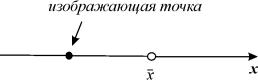
Стационарное состояние (точка покоя, особая точка, состояние равновесия)
В стационарном состоянии значения переменных в системе не меняются со временем. На языке дифференциальных уравнений это означает:
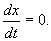
Если левая часть уравнения равна нулю, значит равна нулю и его правая часть:
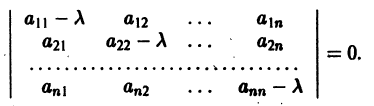
Корни алгебраического уравнения (2.3): 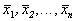
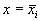
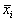
Реальные биологические системы испытывают многочисленные флуктуации, переменные при малых отклонениях возвращаются к своим стационарным значениям. Поэтому при построении модели важно знать, устойчивы ли стационарные состояния модели.
Рис. 2.3. К понятию устойчивости состояния равновесия

Устойчивость состояния равновесия
Каждый имеет интуитивное представление об устойчивости. На рис. 2.3. в обоих положениях (а и б) шарик находится в равновесии, т.к. сумма сил, действующих на него, равна нулю.
Попытайтесь ответить на вопрос : «Какое из этих состояний равновесия устойчиво?»
Скорее всего, Вы дали правильный ответ. Сказать, как Вы догадались? Вы дали шарику малое отклонение от состояния равновесия . В случае ( а) шарик вернулся. В случае ( б) покинул состояние равновесия навсегда.
Устойчивое состояние равновесия можно определить так: если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от особой точки, то особая точка будет устойчивым состоянием равновесия, что соответствует устойчивому режиму функционирования системы.
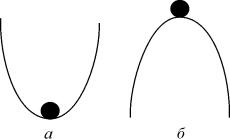
Строгое математическое определение устойчивости состояния равновесия уравнения dx/dt = f( x) выглядит следующим образом :
Состояние равновесия устойчиво по Ляпунову, если задав сколь угодно малое положительное 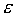
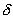
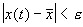
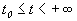
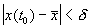
Иначе говоря, для устойчивого состояния равновесия справедливо утверждение: если в момент времени 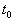
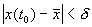
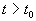
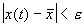
Другими словами: c тационарное состояние называется устойчивым, если малые отклонения не выводят систему слишком далеко из окрестности этого стационарного состояния. Пример — шарик в ямке (с трением или без трения).
Стационарное состояние называется асимптотически устойчивым, если малые отклонения от него со временем затухают. Пример — шарик в ямке в вязкой среде.
Стационарное состояние называется неустойчивым, если малые отклонения со временем увеличиваются. Пример: шарик на горке.
Устойчивое стационарное состояние представляет собой простейший тип аттрактора.
Аттрактором называется множество, к которому стремится изображающая точка системы с течением времени (притягивающее множество).
В нашем курсе мы рассмотрим следующие типы аттракторов:
· устойчивая точка покоя;
· предельный цикл — режим колебаний с постоянными периодом и амплитудой (начиная с размерности системы 2 );
· Области с квазистохастическим поведением траекторий в области аттрактора, например, «странный аттрактор» (начиная с размерности 3 ).
Аналитический метод исследования устойчивости стационарного состояния (метод Ляпунова). Линеаризация системы в окрестности стационарного состояния.
Метод Ляпунова приложим к широкому классу систем различной размерности, точечным системам, которые описываются обыкновенными дифференциальными уравнениями, и распределенным системам, описываемым уравнениями в частных производных, непрерывным и дискретным.
Рассмотрим метод линеаризации Ляпунова для одного автономного дифференциального уравнения первого порядка. Пусть 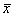
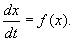
Пусть система, первоначально находившаяся в стационарном состоянии, отклонилась от него и перешла в близкую точку с координатой: 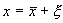

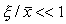
Перейдем в уравнении (2.1) от переменной x к переменной 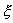
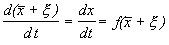
Учтем, что 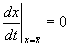
Правую часть разложим в ряд Тейлора в точке 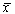
где
Отбросим члены порядка 2 и выше. Останется линейное уравнение:
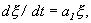
которое носит название линеаризованного уравнения или уравнения первого приближения. Интеграл этого уравнения для 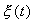
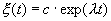
где 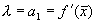
Если SYMBOL 108 f «Symbol» s 12 l SYMBOL 60 f «Symbol» s 12 0 , то при 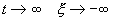
Если же SYMBOL 108 f «Symbol» s 12 l SYMBOL 62 f «Symbol» s 12 > 0 , то при 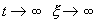
Если SYMBOL 108 f «Symbol» s 12 l =0 , то уравнение первого приближения не может дать ответа на вопрос об устойчивости состояния равновесия системы. Необходимо рассматривать члены более высокого порядка в разложении в ряд Тейлора. Такие случаи мы рассмотрим в лекции 6.
Аналогичные рассуждения проводятся при рассмотрении устойчивости стационарных состояний более сложных динамических систем.
Итак, устойчивость стационарного состояния 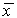
В случае одного уравнения вопрос об устойчивости состояния равновесия нетрудно решить, рассматривая график функции f(x).
По определению в стационарной точке правая часть уравнения (2.1) ‑ функция f(x) обращается в нуль.
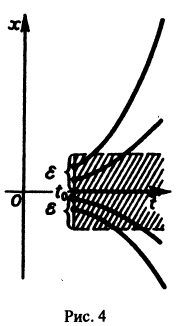
Здесь возможны три случая (рис. 2.4 а, б, в).
1. Вблизи состояния равновесия функция f(x) меняет знак с плюса на минус при возрастании x (рис. 2.4 а).
Отклоним изображающую точку системы в сторону 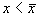
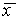
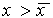
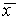
Рис. 2.4. Определение устойчивости стационарного состояния по графику функции f( x)
a – стационарное состояние 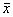
б, в ‑ стационарное состояние 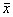
2. Вблизи состояния равновесия функция f ( x) меняет знак с минуса на плюс при возрастании x ( рис. 2.4 б) .
Проведите рассуждения, аналогичные случаю 1. Поместите изображающую точку в область 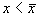
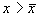
В обоих случаях изображающая точка удаляется от состояния равновесия. Стационарное состояние неустойчиво.
3. Вблизи состояния равновесия функции f(x) не меняет знак ( рис 2.4 в) .
Поскольку 
Вопрос. Является ли состояние равновесия в случае 3 устойчивым?
Ответ. Нет. По определению устойчивости.
1. Рост колонии микроорганизмов
За время D t прирост численности равен:
где R – число родившихся и S – число умерших за время SYMBOL 68 f «Symbol» s 12 D t особей пропорциональные этому промежутку времени:
В дискретной форме:
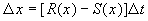
Разделив на SYMBOL 68 f «Symbol» s 12 D t и переходя к пределу при t SYMBOL 174 f «Symbol» s 12 ® 0 , получим дифференциальное уравнение
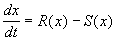
В простейшем случае, когда рождаемость и смертность пропорциональны численности:
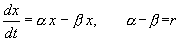
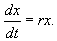
Разделим переменные и проинтегрируем:
Переходя от логарифмов к значениям переменной x и определяя произвольную постоянную С из начальных условий, получим экспоненциальную форму динамики роста.
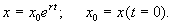
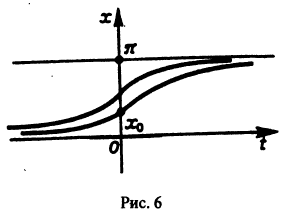
График функции (2.8) при положительных (размножение) и отрицательных (вымирание) значениях константы скорости роста представлен на рис. 2.5. Роль этой модели в развитии математической биологии и экологии мы обсудим в Лекции 3.
Рис. 2.5. Экспоненциальная форма динамики роста численности колонии микроорганизмов в соответствии с системой уравнений (2.7)

2. Вещество переходит в раствор
Пусть количество вещества, переходящего в раствор, пропорционально интервалу времени и разности между максимально возможной концентрацией Р и концентрацией x в данный момент времени: 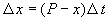
В форме дифференциального уравнения этот закон выглядит в
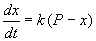
Разделим в этом уравнении переменные, и проинтегрируем:
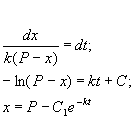
Здесь C 1 — произвольная постоянная. Если x (0) = 0,
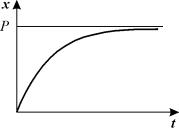
График этой функции представлен на рис. 2.6. – он представляет собой кривую с насыщением.
Рис. 2.6. Концентрация вещества х в зависимости от времени. График уравнения 2.9.

Какие дифференциальные уравнения можно решать аналитически?
Лишь для ограниченных классов дифференциальных уравнений разработаны аналитические методы решения. Подробно они изучаются в курсах дифференциальных уравнений. Отметим основные из них/
1. Уравнения с разделяющимися переменными решаются в интегралах. К ним относятся оба приведенные выше примера.
2. Линейные дифференциальные уравнения (не обязательно автономные).
3. Некоторые специальные виды уравнений.
Решение линейного уравнения
Линейным дифференциальным уравнением 1-го порядка называют уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:
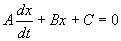
Здесь A, B, C — заданные непрерывные функции от t.
Пусть в некотором интервале изменения t A SYMBOL 185 f «Symbol» s 12 _ 0 . Тогда на него можно разделить все члены уравнения. При этом получим:
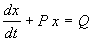
Eсли Q=0 , уравнение (2.12) называется однородным, если Q SYMBOL 185 f «Symbol» s 12 _ 0 – неоднородным.
Решим сначала однородное уравнение.
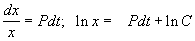
Общее решение линейного однородного уравнения имеет вид:
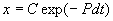
Чтобы найти решение неоднородного уравнения применим метод вариации постоянной. Будем считать С неизвестной функцией t . Подставляя правую часть выражения (2.13) в уравнение (2.12), имеем:
Теперь С находим интегрированием: 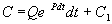
Итак, общее решение линейного неоднородного уравнения первого порядка:
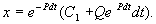
Таким образом, решение уравнения (2.12) представляет собой сумму двух слагаемых:
1) общее решение однородного уравнения (2.13) и
2) частное решение неоднородного уравнения, которое получается из общего решения, если С1 = 0.
Рассмотрим еще один пример, который относится к классическим моделям математической экологии. Логистическое уравнение было предложено Ферхюльстом в 1838 г. Оно имеет вид:
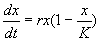
Это уравнение обладает двумя важными свойствами. При малых х численность х возрастает, при больших – приближается к определенному пределу К .
Уравнение (2.15) можно решить аналитически. Ход решения следующий. Произведем разделение переменных:
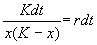
Представим левую часть в виде суммы и проинтегрируем
Переходя от логарифмов к переменным, получим:
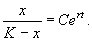
Здесь С – произвольная постоянная, которая определяется начальным значением численности x0 :
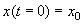
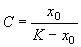
Подставим это значение С в формулу (2.17):
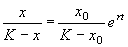
Отсюда получим решение – зависимость численности от времени:
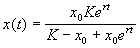
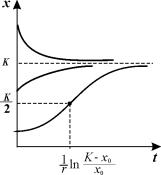
График функции (2.18) при разных начальных значениях численности популяции представлен на рис. 2.7.
Рис.2.7. Динамика численности в логистической модели 2.18
при разных начальных значениях численности

Если начальное значение х0 К/2, кривая роста имеет точку перегиба. Если х0 > К, численность со временем убывает.
В приведенных примерах в правой части уравнений стоят полиномы первой и второй степени. Если в правой части ‑ более сложная нелинейная функция, алгебраическое уравнение для стационарных значений может иметь несколько корней. Какое из этих решений реализуется в этом случае, будет зависеть от начальных условий.
В дальнейшем мы, как правило, не будем искать аналитическое решение для наших моделей. Для более сложных нелинейных уравнений это и невозможно. Однако важные заключения относительно свойств моделей можно сделать и на основании качественного их исследования, в первую очередь путем исследования устойчивости стационарных состояний и типов поведения системы вблизи этих состояний. При этом следует иметь в виду, что с помощью одного автономного дифференциального уравнения могут быть описаны только монотонные изменения переменной, и, следовательно, ни периодические, ни хаотические процессы не могут быть описаны. Для описания более сложного поведения необходимо либо переходить к системам большей размерности (2, 3 порядка и выше), либо вводить время в явном виде в правую часть уравнения. В Лекции 3 мы увидим, что дискретные уравнения и уравнения с запаздыванием могут описать и колебания, и динамический хаос.
- Digiratory
- Лаборатория автоматизации и цифровой обработки сигналов
- Устойчивость нелинейных систем
- Первый метод Ляпунова
- Пример 1.
- Шаг 1. Положение равновесия:
- Шаг 2. Линеаризация для малых отклонений
- Шаг 3. Линеаризованное управление в матричной форме
- Шаг 4. Характеристический полином
- Шаг 5. Корни характеристического полинома
- Заключение об устойчивости системы
- Пример 2. Нелинейный осциллятор
- Шаг 1. Положение равновесия:
- Шаг 2. Линеаризация для малых отклонений
- Шаг 3. Линеаризованное управление в матричной форме
- Шаг 4. Характеристический полином
- Шаг 5. Корни характеристического полинома
- Заключение об устойчивости системы
- Второй метод Ляпунова
- Теорема Ляпунова об устойчивости нелинейных систем
- Пример 3. Нелинейный осциллятор
- Шаг 1. Функция Ляпунова
- Шаг 2. Частные производные
- Шаг 3. Производная функции
- Заключение об устойчивости системы
- Пример 4.
- Шаг 1. Функция Ляпунова
- Шаг 2. Частные производные
- Шаг 3. Производная функции
- Заключение об устойчивости системы
- Теория устойчивости дифференциальных уравнений с примерами решения и образцами выполнения
- Устойчивость по Ляпунову. Основные понятия и определения
- Устойчивость автономных систем. Простейшие типы точек покоя
- Простейшие типы точек покоя
- Метод функций Ляпунова
- Устойчивость по первому (линейному) приближению
- 🎦 Видео
Видео:Математика это не ИсламСкачать

Digiratory
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Лаборатория автоматизации и цифровой обработки сигналов
Видео:Устойчивость 1 ОпределениеСкачать

Устойчивость нелинейных систем
Анализ устойчивости систем является одним из важнейших этапов проектирования систем управления, однако при анализе нелинейных, строго говоря, нет метода отвечающего критериям необходимости и достаточности, а критерии являются, как правило только достаточным (для устойчивости). Исходя из этого, для некоторых систем невозможно однозначно говорить о неустойчивости.
В классической теории управления имеется два основных аналитических метода: первый и второй методы Ляпунова, а также достаточно большое количество модификаций второго метода, как не связанного с линеаризацией.
Рассмотрим применение классических методов Ляпунова.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Первый метод Ляпунова
Позволяет судить об устойчивости положения равновесия по линеаризованным уравнениям. Метод основан на утверждениях:
- если собственные значения линеаризованной системы имеют отрицательные действительные части (линеаризованная система асимптотически устойчива), то положение равновесия нелинейной системы устойчиво «в малом»;
- если среди собственных значений линеаризованной системы имеются «правые», то положение равновесия нелинейной системы неустойчиво;
- если имеются некратные собственные значения на мнимой оси, а остальные — «левые», то в этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.
Таким образом для анализа системы по первому методу Ляпунова необходимо:
- Найти положение равновесия системы — движений в системе нет (т.е. скорости и ускорения равны нулю) [ frac <mathrmv_><mathrmt>= ]
- Линеаризовать систему в окрестности точки равновесия
- Записать полученное линеаризованное дифференциальное уравнение в матричной форме (составить матрицу А)
- Составить характеристический полином линеаризованной системы: [ = ]
- Найти корни характеристического полинома. По виду корней сделать заключение о характере процессов в системе.
Основными недостатками первого метода Ляпунова являются:
- Если имеется корень на мнимой оси, то невозможно сказать о поведении процессов в системе.
- Возможно говорить только об устойчивости «в малом», т.е. при больших отклонениях от положения равновесия система может быть неустойчивой.
Пример 1.
Исследуем систему описываемую дифференциальными уравнениями:
Шаг 1. Положение равновесия:
Для нахождения точек равновесия левые части уравнений приравниваются к 0, что эквивалентно тому, что переменные состояния являются константами, а все их производные равны 0.
Шаг 2. Линеаризация для малых отклонений
Для линеаризации малых отклонений в точке равновесия старшие степени переменных, входящих в уравнения принимаются равными нулю.
Шаг 3. Линеаризованное управление в матричной форме
Преобразуем полученную линейную систему уравнений в матричный вид.
Шаг 4. Характеристический полином
Шаг 5. Корни характеристического полинома
Приравниваем характеристический полином к 0 и находим корни уравнения.
Заключение об устойчивости системы
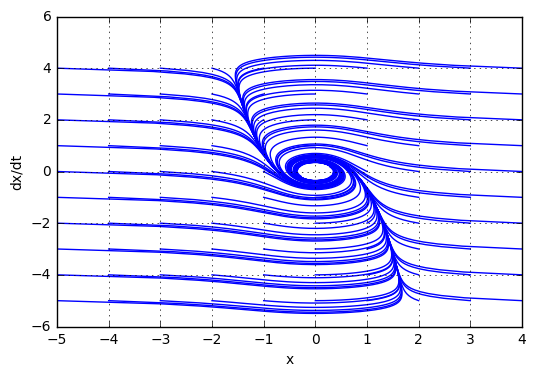
в данном примере при линеаризации система имеет два корня с отрицательной вещественной частью, т.е. мы можем сказать, что система устойчива «в малом» (при больших отклонениях система может быть неустойчива).
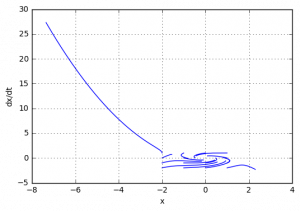
Подтвердим теоретический вывод компьютерным моделированием (построением фазового портрета)
При этом, при начальных условиях, находящиеся дальше от точки равновесия, система становится неустойчивой
Пример 2. Нелинейный осциллятор
В качестве второго примера рассмотрим нелинейный осцилятор описываемый системой дифференциальных уравнений:
Аналогично первому примеру выполняем последовательность шагов
Шаг 1. Положение равновесия:
Шаг 2. Линеаризация для малых отклонений
Шаг 3. Линеаризованное управление в матричной форме
Шаг 4. Характеристический полином
Шаг 5. Корни характеристического полинома
Заключение об устойчивости системы
Рассматриваемая система является критическим случаем о ее устойчивости невозможно судить по линеаризованным уравнениям, применяемым в первом методе Ляпунова.
Видео:Системы дифференциальных уравненийСкачать

Второй метод Ляпунова
Второй метод Ляпунова не связан с линеаризацией системы, поэтому также называется прямым методом.
Для начала необходимо ввести понятия знакоопределенной, знакопостоянной и знакопеременной функций. Пусть имеется функция нескольких переменных:
Функция (V ) называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат
[ left ( Vleft ( bar right )=0 right ) ]
Функция (V ) называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Функция (V ) называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.
Теорема Ляпунова об устойчивости нелинейных систем
Если при заданных в форме
уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова
чтобы ее производная по времени
тоже была знакоопределенной (или знакопостоянной), но имела знак противоположный знаку (V), то данная система устойчива.
Для упрощения скажем, что функция Ляпунова должна быть положительной знакоопределенной функцией. Тогда условия теоремы Ляпунова будут выглядеть следующим образом:
Для устойчивости положения равновесия достаточно существования дифференцируемой функции
называемой функцией Ляпунова, удовлетворяющей в окрестности начала координат следующим условиям:
- (Vleft ( v_, v_,…, v_right ) geq 0) причем (V=0) лишь при следующем условии, означающем что функция (V) имеет строгий минимум в начале координат. [ bar= begin v_ \ vdots \ v_ end = bar ]
- Производная функции по времени [ frac <mathrmVleft ( bar right )><mathrmt>=sum_^frac<partial v_>frac <mathrmv_><mathrmt>=begin frac<partial v_> & frac<partial v_> & cdots & frac<partial v_>endbeginfrac <mathrmv_><mathrmt>\ frac <mathrmv_><mathrmt>\ vdots \ frac <mathrmv_><mathrmt>end ] в силу дифференциального уравнения (frac <mathrmbar><mathrmt>=barleft ( bar right ) ) является отрицательной знакопостоянной функцией, т.е. [ frac <mathrmVleft ( bar right )><mathrmt>=gradbarcdot frac <mathrmbar><mathrmt>=gradbarcdot barleft ( bar right )leq 0 ] при (tgeq t_)
Таким образом, условия:
- (frac <mathrmVleft ( bar right )><mathrmt>leq 0) и функция (Vleft ( v_, v_,…, v_right ) ) является положительной знакоопределенной — это является достаточным условием устойчивости
- (frac <mathrmVleft ( bar right )><mathrmt> ) — отрицательно определенная — это является достаточным условием асимптотической устойчивости.
- (left | v right |rightarrow infty : frac <mathrmVleft ( bar right )><mathrmt>rightarrow infty ) — достаточное условие устойчивости «в целом».
Для анализа системы по второму методу Ляпунова необходимо:
- Выбрать функцию Ляпунова от n переменных, где n- порядок системы.
- Найти частные производные по переменным.
- Вычислить производную функции по времени (frac <mathrmVleft ( bar right )><mathrmt>). Проанализировать полученный знак производной.
Из-за того, что второй метод Ляпунова не связан с линеаризацией, он считается универсальным. Однако он имеет ряд недостатков:
- Нет общих требований по выбору функции V
- Достаточный характер утверждения (если условия не выполняются, то об устойчивости ничего сказать нельзя, а можно посоветовать подобрать другую функцию (V ))
Пример 3. Нелинейный осциллятор
Проанализируем систему из примера (2).
Шаг 1. Функция Ляпунова
Для начала необходимо выбрать функцию Ляпунова от 2-х переменных (т.к. два вектора состояния):
Шаг 2. Частные производные
Шаг 3. Производная функции
Подставим в выражение значения исходя из ДУ:
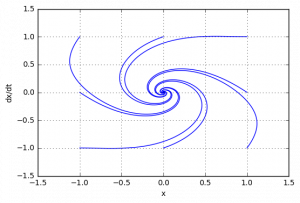
Заключение об устойчивости системы
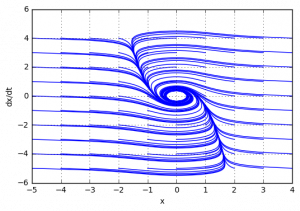
Исследовав систему первым методом Ляпунова мы не смогли сделать конкретный вывод об устойчивости системы, что позволил нам сделать второй метод Ляпунова. В результате мы можем сделать вывод, что система является асимптотически устойчивой.
Аналогично проверим с помощью моделирования:
Пример 4.
Рассмотрим систему, описываемую следующей системой дифференциальных уравнений:
Очевидно, что применение первого метода Ляпунова невозможно, т.к. матрица А состоит из нулей, а, следовательно, собственные значения равны нулю. Поэтому применим второй метод Ляпунова:
Шаг 1. Функция Ляпунова
Выбор функции Ляпунова второго порядка
Шаг 2. Частные производные
Шаг 3. Производная функции
При (a=3) имеет место асимптотическая устойчивость.
Заключение об устойчивости системы
Система является устойчивой.
Фазовый портрет системы выглядит следующим образом:
Видео:Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Теория устойчивости дифференциальных уравнений с примерами решения и образцами выполнения
Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных. Пусть дана задача Коши
Если функция f(t, х) непрерывна по совокупности аргументов и имеет ограниченную производную 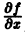
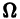
Справедлива следующая теорема о непрерывной зависимости решения от начальных условий.
Теорема:
Если правая часть f(t, х) дифференциального уравнения
непрерывна по совокупности переменных и имеет ограниченную частную производную 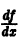
удовлетворяющее начальному условию 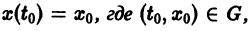
Иными словами, пусть через точку 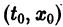
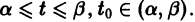
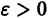
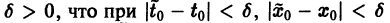
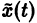
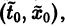
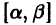
Аналогичная теорема справедлива и для системы дифференциальных уравнений
При выполнении условий теоремы (1) решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то обстоятельство, что отрезок [а, b] изменения t конечен. Однако во многих задачах нас интересует зависимость решения от начальных данных в бесконечном промежутке 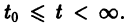
Остановимся вкратце на понятии о продолжаемости решения. Пусть имеем систему дифференциальных уравнений
где t — независимая переменная (время); 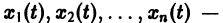
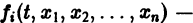
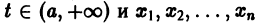
в их области определения непрерывны по совокупности аргументов и имеют ограниченные частные производные по 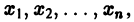
для каждой системы значений
существует единственное решение
системы (3), определенное в некотором интервале 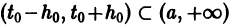
Введем следующее понятие. Пусть
— решение задачи Коши (3)-(4), определенное на некотором интервале I = (t1,t2). Это решение может бьггь продолжено, вообще говоря, на больший интервал времени. Решение
называется продолжением решения 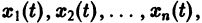
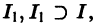
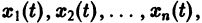
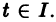
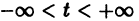
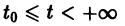
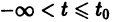
Для дальнейших рассмотрений важен вопрос о существовании решения хi(t), 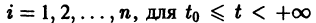
где 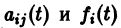
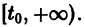
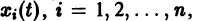
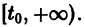
Не все системы обладают таким свойством. Например, для скалярного уравнения
непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция
является решением задачи
Однако это решение существует только в интервале 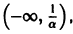
Уравнение (5) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).
Задача:
Показать, что решения уравнения
нельзя продолжить неограниченно ни вправо, ни влево.
Видео:Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

Устойчивость по Ляпунову. Основные понятия и определения
Рассмотрим дифференциальное уравнение первого порядка
где функция f(t,x) определена и непрерывна для 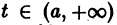
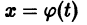
есть решение уравнения (1), удовлетворяющее начальному условию
Пусть, далее, функция
есть решение того же уравнения, удовлетворяющее другому начальному условию
Предполагается, что решения 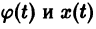
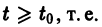
Определение:
Решение 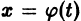
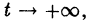
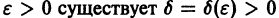
для всех 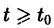
Это значит, что решения, близкие по начальным значениям к решению 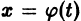
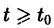
уравнения (1) устойчиво, если, какой бы узкой ни была е-полоска, содержащая кривую 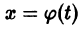
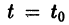
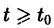
Если при сколь угодно малом 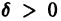
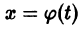
Определение:
Решение 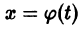
1) решение 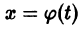
2) существует 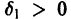
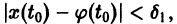
Это означает, что все решения х = x(t), близкие по начальным условиям к асимптотически устойчивому решению 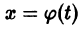
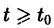
Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.
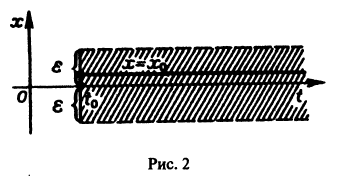
Пример:
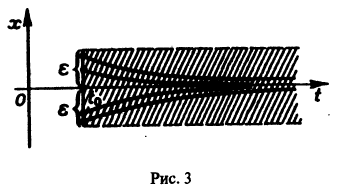
Исследовать на устойчивость тривиальное решение
Решение 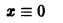
Решение уравнения (*), удовлетворяющее начальному условию
Легко видеть (рис. 2), что, какова бы ни была 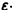
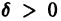
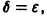
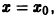
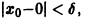
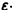
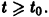
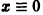
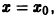
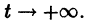
Пример:
Исследовать на устойчивость тривиальное решение 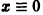
Решение уравнения (**), удовлетворяющее начальному условию
Возьмем любое 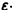
Поскольку 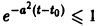
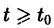
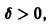
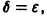
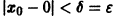
Согласно определению (1) это означает, что решение 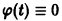
поэтому решение 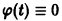
Пример:
Показать, что решение
В самом деле, при сколь угодно малом 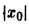
этого уравнения не удовлетворяет условию
при достаточно больших t > to. Более того, при любых 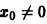
Рассмотрим теперь систему дифференциальных уравнений
где функции fi определены для 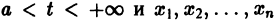
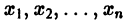
Определение:
системы (4) называется устойчивым по Ляпунову при 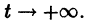
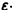
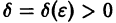
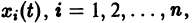
для всех 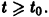
Если при сколь угодно малом 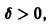
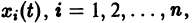
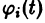
Определение:
системы (4) называется асимптотически устойчивым, если:
1) решение это устойчиво;
2) существует 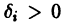
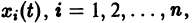
Пример:
Исходя из определения устойчивости по Ляпунову, показать, что решение системы
удовлетворяющее начальным условиям
устойчиво.
Решение системы (*), удовлетворяющее начальным условиям (**), есть
Решение этой системы, удовлетворяющее условиям 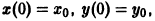
Возьмем произвольное 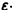
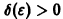
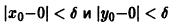
для всех 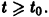
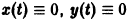
то при 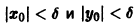
для всех 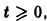
Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим, например, уравнение
Решением этого уравнения, удовлетворяющим условию х(0) = 0, является функция
Решение, удовлетворяющее начальному условию 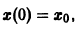
Геометрически очевидно (рис.5), что для всякого 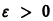
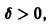
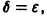
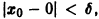
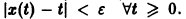
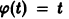
Из ограниченности решений дифференциального уравнения не следует устойчивости решений.
Рассмотрим уравнение
Оно имеет очевидные решения
Интегрируя уравнение (6), находим
Все решения (7) и (8) ограничены на 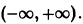
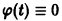
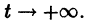
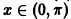
Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.
Замечание:
Исследуемое на устойчивость решение
системы (4) всегда можно преобразовать в тривиальное решение
другой системы заменой
В самом деле, пусть имеем (для простоты) одно дифференциальное уравнение
и пусть требуется исследовать на устойчивость какое-либо решение 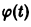
(величину 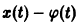
и подстановка в (*) приводит к равенству
Но 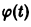
Обозначив здесь правую часть через F(t, у), получим
Это уравнение имеет решение 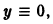
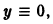
Таким образом, вопрос об устойчивости решения 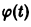
Видео:Урок 5 - Дифференциальные уравнения, системы диффуровСкачать

Устойчивость автономных систем. Простейшие типы точек покоя
Нормальная система дифференциальных уравнений называется автономной, если ее правые части fi не зависят явно от t, т. е. если она имеет вид
Это значит, что закон изменения неизвестных функций, описываемый автономной системой, не меняется со временем, как это бывает с физическими законами. Пусть имеем автономную систему
и пусть (а1, a2, …, аn) — такая совокупность чисел, что
Тогда система функций
будет решением системы (1). Точку 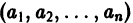
есть точка покоя этой системы. Обозначим через S(R) шар
и будем считать, что для рассматриваемой системы в шаре S(R) выполнены условия теоремы существования и единственности решения задачи Коши.
Определение:
Будем говорить, что точка покоя
системы (1) устойчива, если для любого 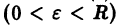
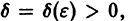
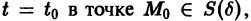
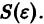
1) она устойчива;
2) существует такое 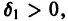
Поясним это определение примерами.
Пример:
Траектории здесь — концентрические окружности
с центром в начале координат — единственной точкой покоя системы. Если взять 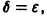
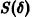
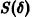
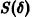
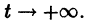
Пример:
Пусть дана система
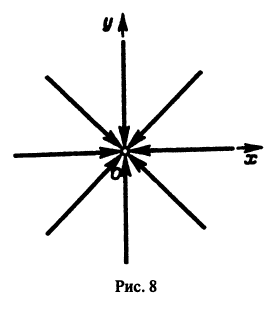
поэтому траекториями являются лучи, входящие в начало координат (рис.8). Можно снова выбрать 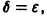
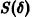
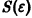
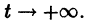
Пример:
Возьмем, наконец, систему
и траекториями являются лучи, исходящие из начала координат, но в отличие от примера 2 движение по лучам происходит в направлении от центра. Точка покоя неустойчива.
Видео:Размышляю над Хаосом и Равновесием - ДиффурыСкачать

Простейшие типы точек покоя
Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:
Решение будем искать в виде
Для определения 
Величины 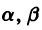
Возможны следующие случаи.
А. Корни 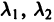
- Пусть
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
все точки каждой траектории, находившиеся в начальный момент
в произвольной
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, а при
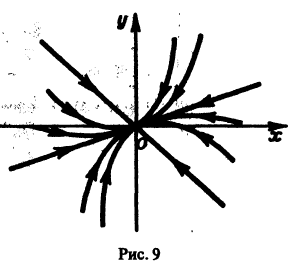
стремятся к этому началу. Такая точка покоя называется устойчивым узлом
При С2 = 0 из (4) получаем
и траекториями являются два луча, входящие в начало координат с угловым коэффициентом
Аналогично, при С1 = 0 получаем еще два луча, входящие в начало координат с угловым коэффициентом
Пусть теперь 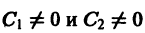
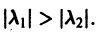
т. е. все траектории (исключая лучи 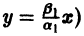
2. Если 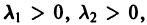
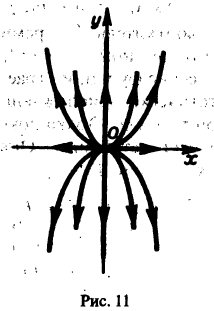
Пример:
Для нее точка О(0,0) — точка покоя. Характеристическое уравнение
имеет корни 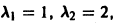
Оно имеет решения
так что траекториями системы будут лучи падающие с координатными полуосями, семейство парабол, касающихся оси Oх в начале координат (рис. 11)
3. Пусть теперь 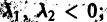
При С2 = 0 получаем решение
С возрастанием t точка этой траектории движется по лучу
в направлении от начала 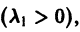
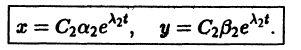
Отсюда видно, что при возрастании t точка движется по лучу
в направлении к началу координат 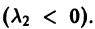
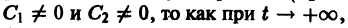
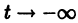
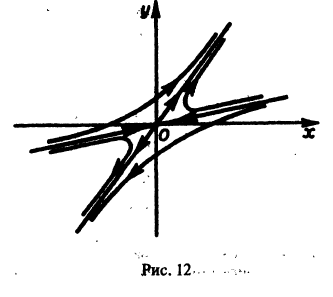
Пример:
Исследуем характер точки покоя О(0,0) системы
Характеристическое уравнение системы
имеет корни 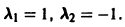
интегрируя которое получаем
Уравнение (6) имеет также решения
Таким образом, интегральные кривые этого уравнения (траектории системы (5)) — равнобочные гиперболы и лучи, совпадающие с координатными полуосями.
Б. Корни 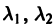
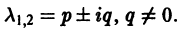
где C1 и C2 — произвольные постоянные, а 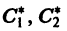
- Пусть
в этом случае множитель
стремится к нулю при
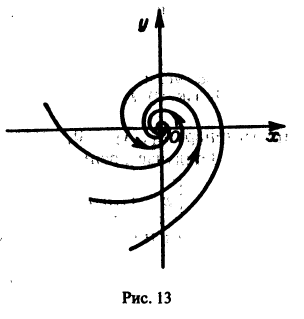
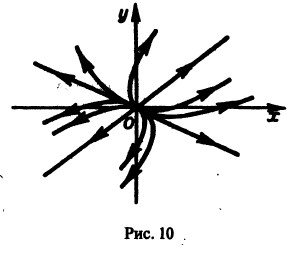
а вторые множители в (7) — ограниченные периодические функции. Траектории — спирали, асимптотически приближающиеся к началу координат при
Точка покоя х = 0, у = 0 асимптотически устойчива. Она называется устойчивым фокусом (рис. 13).,
- Если
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
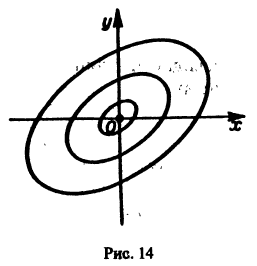
- Если же
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
не стремится к нулю при
Пример. Рассмотрим систему уравнений
Характеристическое уравнение системы
имеет комплексные корни
Перейдем от системы к одному уравнению
и введем полярные координаты 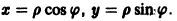
Используя уравнение (9), находим, что
Эти интегральные кривые являются логарифмическими спиралями, навивающимися на начало координат, которое достигается в пределе при 
Интегральные кривые этого уравнения — окружности с центром в начале координат, которое при а = 0 является точкой покоя системы (8) типа центра.
В. Корни 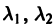
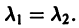
( 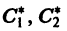
- Если
то из-за наличия множителя
решения х(t), y(t) стремятся к нулю при
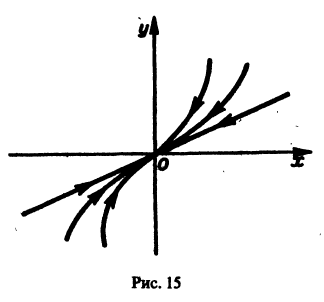
Точка покоя х = 0, у = 0 асимптотически устойчива. Ее называют устойчивым вырожденным узлам (рис. 15). Он отличается от узла в случае А. 1 (там одна из траекторий имела касательную, отличную от всех остальных). Возможен также дикритический узел (см. рис. 8).
- При
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
Пример:
Для системы уравнений
имеет кратные корни 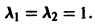
Поэтому все интегральные кривые проходят через начало координат, и все они имеют там ось Оу общей касательной.
Мы перебрали и исчерпали все возможности, поскольку случай 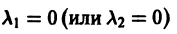
Пример:
Исследовать уравнение малых колебаний маятника с учетом трения.
Уравнение малых колебаний маятника в этом случае имеет вид
где x — угол малого отклонения маятника от вертикали, к — коэффициент трения. Заменим уравнение (*) эквивалентной системой
Характеристическое уравнение для системы (**)
Если 0
— частота колебаний, а величины А, а определяются из начальных условий.
График решения и фазовая кривая при 0
Сформулируем результаты, касающиеся устойчивости решений системы п линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами
Рассмотрим для системы (10) характеристическое уравнение
Справедливы следующие предложения:
1) если все корни характеристического уравнения имеют отрицательную действительную часть, то все решения системы (10) асимптотически устойчивы. Действительно, в этом случае все слагаемые общего решения содержат множители 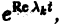
2) если хотя бы один корень 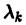
3) если характеристическое уравнение имеет простые корни с нулевой действительной частью (т. е. чисто мнимые или равные нулю корни), а остальные корни, если они есть, имеют отрицательную действительную часть, та все решения устойчивы, но асимптотической устойчивости нет.
Эти результаты относятся и к одному линейному дифференциальному уравнению с постоянными коэффициентами.
Следует обратить внимание на то, что для линейной системы все решения либо устойчивы, либо неустойчивы одновременна
Теорема:
Решения Системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Преобразуем произвольное частное решение
системы (11) в тривиальное с помощью замены
Система (11) преобразуется при этом в линейную однородную систему относительно yi(t):
Следовательно, все частные решения системы (11) в смысле устойчивости ведут себя одинаково, а именно как тривиальное решение однородной системы (12).
В самом деле, пусть тривиальное решение
системы (12) устойчиво. Это значит, что для любого 
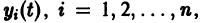
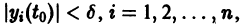
Замечая, что 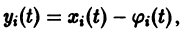
для всякого решения 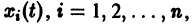
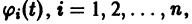
Это предложение не имеет места для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.
Пример:
Рассмотрим нелинейное уравнение
Оно имеет очевидные решения
Решение x(t) = -1 неустойчиво, а решение x(t) = 1 является асимптотически устойчивым. В самом деле, при 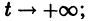
стремятся к +1. Это означает, согласно определению, что решение x(t) = 1 асимптотически устойчиво.
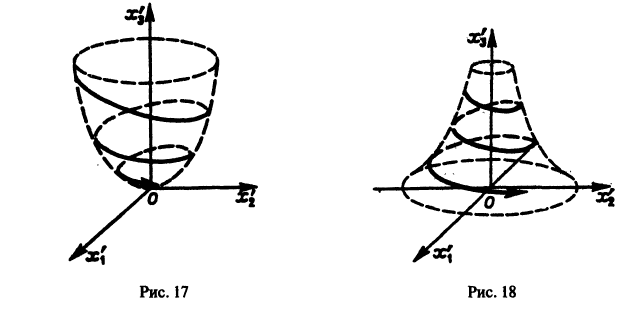
Замечание:
Как и в случае n = 2, можно исследовать расположение траекторий в окрестности точки покоя О(0,0,0) системы (10). Для n = 3 возможны так называемые узлофокусы (рис. 17), седлофокусы (рис. 18) и т. д.
Видео:ОДУ. 4 Системы дифференциальных уравненийСкачать

Метод функций Ляпунова
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции 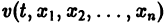
Ограничимся рассмотрением автономных систем
для которых Xi = 0, i = 1, 2,…, n, есть точка покоя.
Идея метода состоит в следующем. Предположим, что на устойчивость исследуется точка покоя 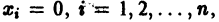
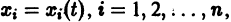
(производная вдоль траектории): Правая часть в (2) есть известная функция от х1, х2,…, хn, и можно исследовать ее знак. Если окажется, что 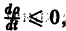
Определение:
Функция v(x1, х2, … xn), определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрицательной), если в области G
где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при
Так, в случае n = 3 функции
будут знакоположительными, причем здесь величина h > 0 может быть взята сколь угодно большой.
Определение:
Функция 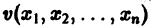
будет знакопостоянной (положительной). В самом деле, функцию v(x1, x2, x3) можно представить так:
отсюда видно, что она неотрицательна всюду, но обращается в нуль и при 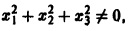
Пусть 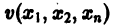
являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции v повремени имеем
Определение:
Величина 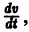
Определение:
Функций 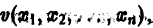
1) 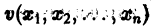
2) 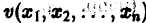
3) полная производная 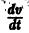
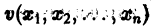
всюду в 
Теорема:
Теорема Ляпунова об устойчивости. Если для системы дифференциальных уравнений
существует дифференцируемая знакоопределенная функция 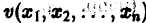
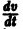
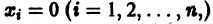
Приведем идею доказательства. Пусть для определенности 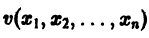
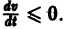
причем v = 0 лишь при 
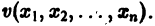
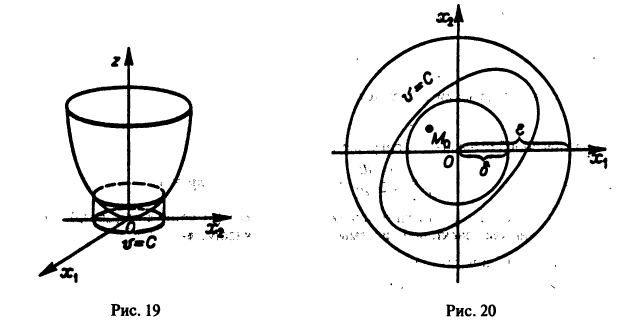
функции v являются, Как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае n = 2. Так как 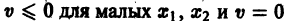
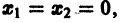
в общих чертах напоминает параболоид, вогнутый Вверх (рис. 19).
Линии уровня 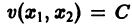
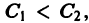
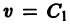
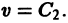
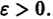
существует дифференцируемая знакоопределенная функция 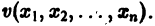
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Выберем в качестве функции v(x, y) функцию
Эта функция знакоположительная. В силу системы (*) найдем
Из теоремы 3 следует, что точка покоя О(0,0) системы (*) устойчива (центр). Асимптотической устойчивости нет, так как траектория системы (*) — окружности.
Пример 2. Исследовать на устойчивость точку покоя О(0,0) системы
Таким образом, 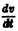
Теорема:
О неустойчивости. Пусть для системы дифференциальных уравнений
существует дифференцируемая в окрестности начала координат функция 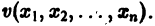
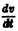
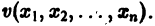
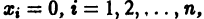
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Для нее функция
знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, 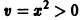
Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет. В простейших случаях функцию Ляпунова можно искать в виде
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Устойчивость по первому (линейному) приближению
Пусть имеем систему дифференциальных уравнений
и пусть 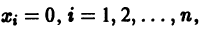
Будем предполагать, что функции 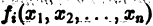
а слагаемые Ri содержат члены не ниже второго порядка малости относительно 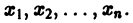
Так как понятие устойчивости точки покоя O(0,0,…, 0) связано с малой окрестностью начала координа’т в- фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по х. Поэтому наряду с системой (3) рассмотрим систему
называемую системой уравнений первого (линейного) приближения для системы (3).
Вообще говоря, строгой связи между системами (3) и (4) нет. Рассмотрим, например, уравнение
Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид
Решение 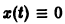
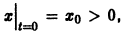
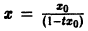
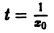
Теорема:
Если все корни характеристического уравнения
имеют отрицательные действительные части, то точка покоя 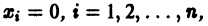
При выполнении условий теоремы возможно исследование на устойчивость по первому приближению.
Теорема:
Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя Xi= 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению.
Наметим идею доказательства теорем 6 и 7.
Пусть для простоты корни 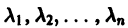
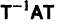
где 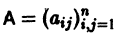
и система (4) преобразуется к виду
или, в силу выбора матрицы Т,
Система (3) при том же преобразовании перейдет в систему
причем в 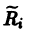
Рассмотрим следующие возможности:
1. Все корни 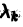
тогда производная 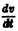
где 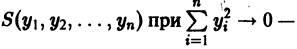
Таким образом, в достаточно малой окрестности 
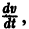
2. Некоторые из корней 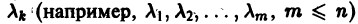
Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых 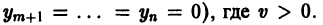
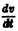
В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример:
Исследовать на устойчивость по первому приближению точку покоя х = 0, у = 0 системы
Система первого приближения имеет вид
Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы (**):
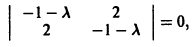
Корни характеристического уравнения 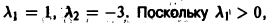
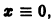
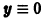
Пример:
Исследуем на устойчивость точку покоя О(0, 0) системы
Точка покоя х = 0, у = 0 системы (*) асимптотически устойчива, так как для этой системы функция Ляпунова
удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя х = 0, у = 0 системы
В самом деле, для функции 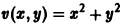
т.е. 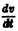
В силу теоремы 5 заключаем о неустойчивости точки покоя О(0,0) системы (**).
Для системы (*) и (**) система первого приближения одна и та же:
для системы (***) имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю). Для системы первого приближения (***) начало координат является устойчивой точкой покоя — центром. Системы (*) и (**) получаются малым возмущением правых частей (***) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя О(0,0) становится асимптотически устойчивой, а для системы (**) неустойчивой.
Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Задача. Исследовать на устойчивость точку покоя О(0,0) системы
где функция f(х,у) разлагается в сходящийся отеленной ряд и f(0,0) = 0.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎦 Видео
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Филиппов №881(г) — Исследование решения на устойчивостьСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Устойчивость положений равновесия. Дифференциальные уравнения, ВШЭ-РЭШ, 2022-04-12.Скачать

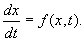
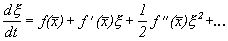
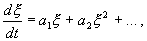
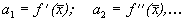

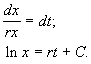
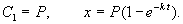
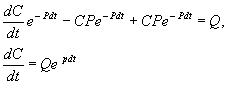
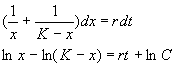

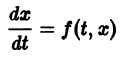
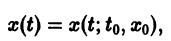
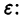
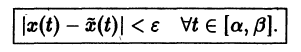
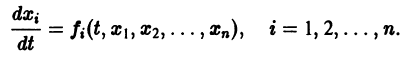
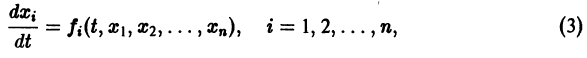
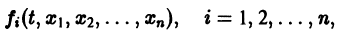
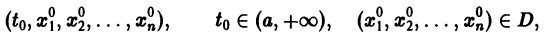
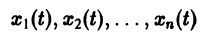
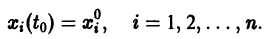
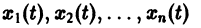
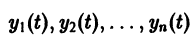
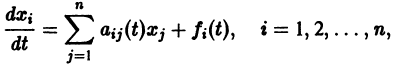
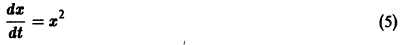
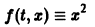
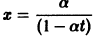
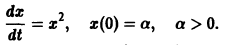
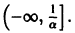
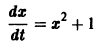


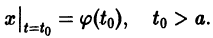
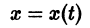
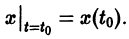


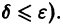

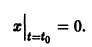
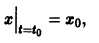
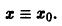
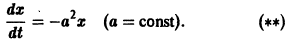
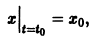
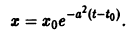
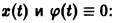
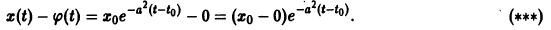
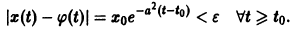
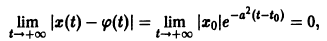
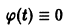
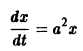
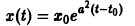
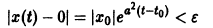
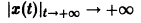
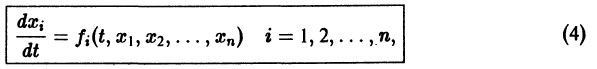
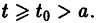
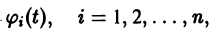
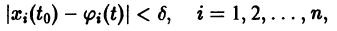
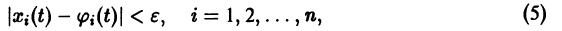
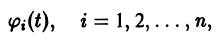
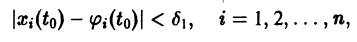
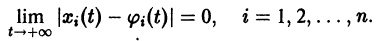


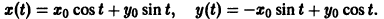
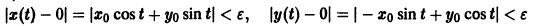
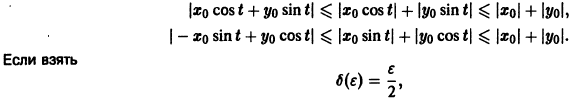
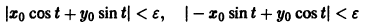
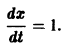
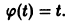
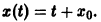


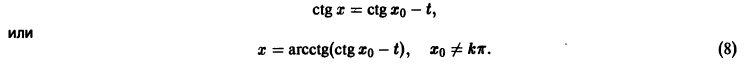
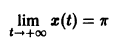
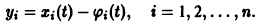

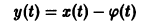
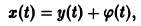

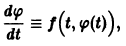
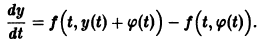

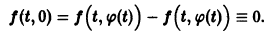
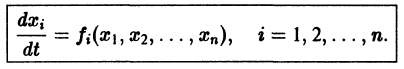
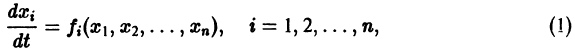
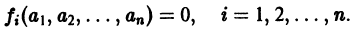
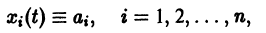
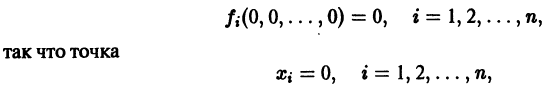
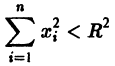
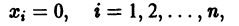
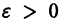
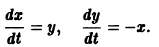
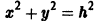
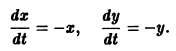
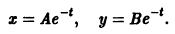
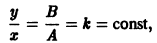
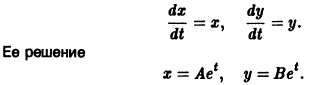
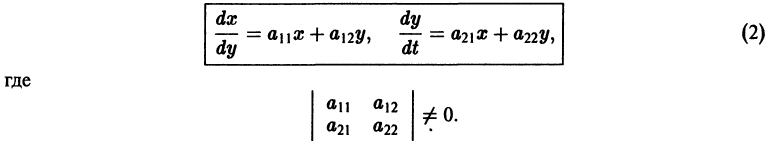
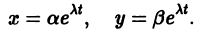
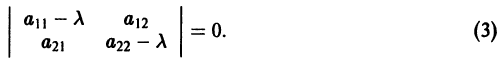
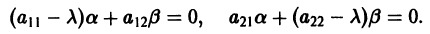
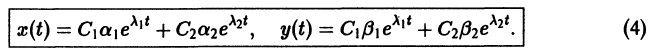
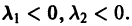 Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей 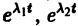 все точки каждой траектории, находившиеся в начальный момент
все точки каждой траектории, находившиеся в начальный момент  в произвольной
в произвольной  окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой, 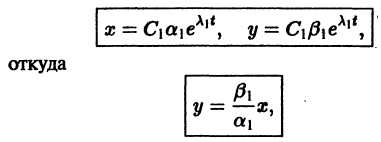
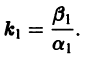
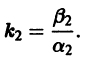
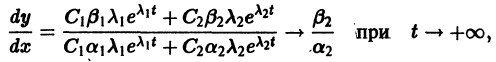
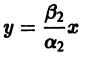
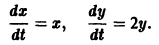
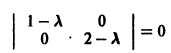
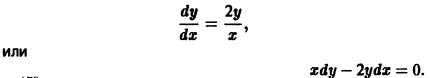

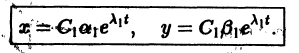
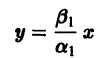
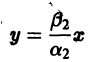
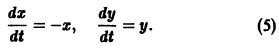
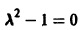
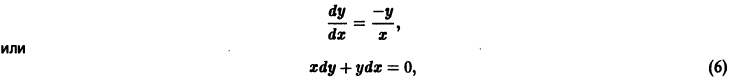
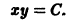
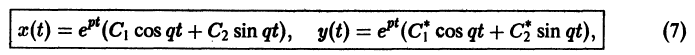
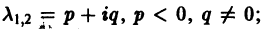 в этом случае множитель
в этом случае множитель 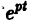 стремится к нулю при
стремится к нулю при 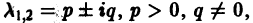 то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.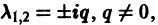 то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение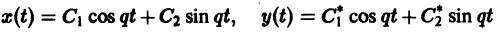
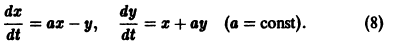
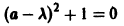
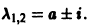

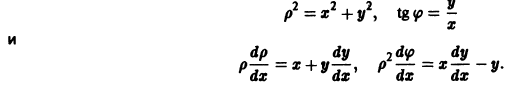
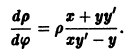

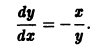
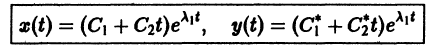
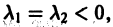 то из-за наличия множителя
то из-за наличия множителя 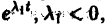 решения х(t), y(t) стремятся к нулю при
решения х(t), y(t) стремятся к нулю при 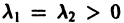 замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.