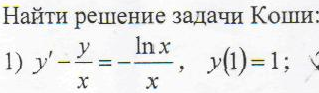Найти решение задачи коши для уравнения если

Видео:Пример 65. Решить задачу Коши (диффуры)Скачать

Задача Коши онлайн

Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.

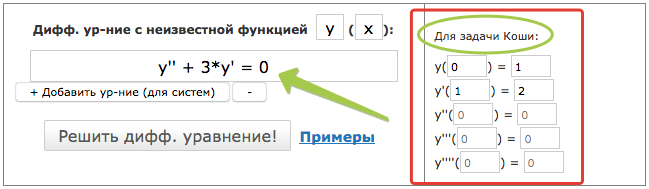
Найти решение задачи Коши для дифференциального уравнения:

при заданных начальных условиях:

При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .

Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:

удовлетворяющее начальным условиям:

Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:

Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:

Далее, поставляем начальные условия в функцию и её производную :

Решая полученную систему уравнений получаем значения произвольных постоянных и :

Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:

Видео:Задача Коши ДУ I п. 1. Caushy`s ProblemСкачать

Другие полезные разделы:

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме

Видео:Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

Решение задачи Коши

Онлайн калькулятор для решения задачи Коши. Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Для того чтобы решить задачу Коши необходимо найти общее решение дифференциального уравнения, а потом подставить начальные условия и найти неизвестные коэффициенты С1 и С2.
Данный калькулятор решает задачу Коши для дифференциального уравнения второго порядка.
В калькулятор вводим дифференциальное уравнение и начальные условия, как указано в примере, нажимаем кнопку «Вычислить», получаем ответ.

Видео:2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать

Найти решение задачи коши для уравнения если

Рассмотрим пример решения задачи Коши с помощью онлайн калькулятора «Контрольная-работа.Ру».

Внимание! Следуя этому примеру и подробно и внимательно читая вы сможете решить и свою задачу, просто следуя тем же шагам!

Возьмём задачу из контрольной «Решить задачу Коши для дифференциального уравнения второго порядка«:

Для того, чтобы решить данную задачу откройте сервис решения дифференциальных уравнений онлайн

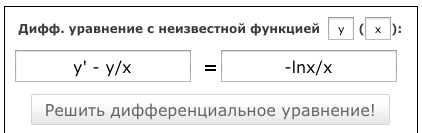
и введите в форму левую часть уравнения y’ — y/x

а в правую часть уравнения: -lnx/x

как на картинке:

Нажимаем кнопку «Решить дифференциальное уравнение!«

Видим ответ для этого дифф. ур-ния:

Но как вы знаете, это ещё не решение задачи Коши, это всего лишь решение дифференциального уравнения.

Теперь по начальным условиям y(1) = 1 надо найти C1.

Для этого воспользуемся сервисом по решению обычных уравнений онлайн

Вобъём в форму обычных уравнений в правую часть уравнения c*x + log(x) + 1, а в левую y

А также укажем, что уравнение с неизвестной c=C1

На рис. всё это видно:

Нажимаем кнопку «Решить уравнение!«

Получаем ответ для C1

Но и это ещё не всё.

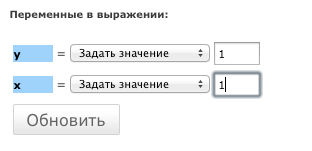
Надо указать, что y = 1 и x = 1 (т.к. y(1)=1). Подставляем по той же ссылке как на рис. ниже:

Нажимаем кнопку «Обновить«

И получаем окончательный ответ для C1:

Подставляем это C1 в решение дифф. уравнения и мы получим решение нашей задачи Коши:

Тэги: уравнение

© Контрольная работа РУ — примеры решения задач

🎬 Видео

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решить задачу КошиСкачать

Задача Коши для дифференциальных уравненийСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Задача Коши для системы д. у.Скачать

Задача Коши для ЛНДУ II п. (e^x)Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Решение задачи Коши дифференциального уравнения #maths #calculus #differentialequation #algebraСкачать

Операционный метод для задачи КошиСкачать

Метод ЭйлераСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

5.1 Задача Коши для уравнений теплопроводности IСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать