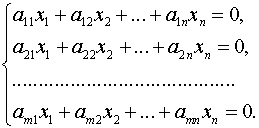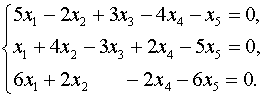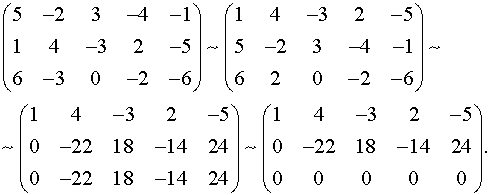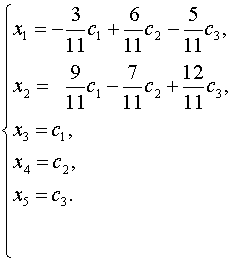Найти размерность и базис векторного пространства решений системы однородных линейных уравнений (5 видео)

Содержание

Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3
Системы линейных однородных уравнений
Векторное пространство: размерность и базис, разложение вектора по базису
Разложение вектора по базису
Связь между базисами
Системы линейных однородных уравнений
Свойства систем линейных однородных уравнений
Линейные пространства. Подпространства
Системы линейных однородных уравнений
Понятие размерности векторного пространства и базиса.
Разложение вектора по базису векторного пространства.
Связь между базисами.
Примеры базисов линейных пространств
💥 Видео

Видео:Линейная оболочка. Базис и размерностьСкачать

Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3

Системы линейных однородных уравнений

Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы

1. Записываем матрицу системы:

и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:

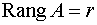
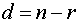
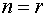
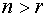
Размерность пространства решений равна . Если , то однородная система имеет единственное нулевое решение, если , то система имеет бесчисленное множество решений.

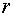
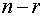
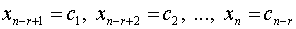
2. Выбираем базисных и свободных переменных. Свободные переменные обозначаем . Затем базисные переменные выражаем через свободные, получив таким образом общее решение однородной системы линейных уравнений.

3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.

Примечание. К элементарным преобразованиям матрицы относят:

1. умножение (деление) строки на множитель, отличный от нуля;

2. прибавление к какой-либо строке другой строки, умноженной на любое число;

3. перестановка строк местами;

4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).

Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.

Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:

Полагаем , тогда

Размерность линейного пространства решений равна 3.

:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Видео:Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Системы линейных однородных уравнений

Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Видео:Неоднородная система линейных уравненийСкачать

Свойства систем линейных однородных уравнений

Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.

Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.

Видео:Базис линейного пространства (01)Скачать

Линейные пространства. Подпространства

Время на чтение: 35 минут

Системы линейных однородных уравнений

Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы

1. Записываем матрицу системы:

Примечание. К элементарным преобразованиям матрицы относят:

1. умножение (деление) строки на множитель, отличный от нуля;

2. прибавление к какой-либо строке другой строки, умноженной на любое число;

3. перестановка строк местами;

Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.

Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:

P и A – подмножество из L . Если A само составляет линейное пространство над полем P относительно тех же операций, что и L , то A называют подпространством пространства L .

Согласно определению линейного пространства, чтобы A было подпространством надо проверить выполнимость в A операций:

1) :
;

2)
:
;

и проверить, что операции в A подчинены восьми аксиомам. Однако последнее будет излишним (в силу того, что эти аксиомы выполняются в L) т.е. справедлива следующая

Теорема. Пусть L линейное пространство над полем P и
. Множество A тогда и только тогда является подпространством L, когда выполняются следующие требования:

Утверждение. Если L – n -мерное линейное пространство и A его подпространство, то A также конечномерное линейное пространство и его размерность не превосходит n .

Пример 1. Является ли подпространством пространства векторов-отрезков V 2 множество S всех векторов плоскости , каждый из которых лежит на одной из осей координат 0x или 0y?

Решение : Пусть
,
и
,
. Тогда
. Следовательно, S не является подпространством .

Пример 2. Является ли линейным подпространством линейного пространства V 2 векторов-отрезков плоскости множество S всех векторов плоскости, начала и концы которых лежат на данной прямой l этой плоскости?

Если вектор
умножить на действительное число k , то получим вектор
, также принадлежащий S. Если и – два вектора из S, то
(по правилу сложения векторов на прямой). Следовательно, S является подпространством .

Пример 3. Является ли линейным подпространством линейного пространства V 2 множество A всех векторов плоскости, концы которых лежат на данной прямой l , (предположить, что начало любого вектора совпадает с началом координат)?

Решение.

В случае, когда прямая l не проходит через начало координат множество А линейным подпространством пространства V 2 не является, т.к.
.

В случае, когда прямая l проходит через начало координат, множество А является линейным подпространством пространства V 2 , т.к.
и при умножении любого вектора
на действительное число α из поля Р получим
. Таким образом , требования линейного пространства для множества А выполнены.

Пример 4. Пусть дана система векторов
из линейного пространства L над полем P . Доказать, что множество всевозможных линейных комбинаций
с коэффициентами
из P является подпространством L (это подпространство A называют подпространством, порожденным системой векторов или линейной оболочкой этой системы векторов , и обозначают так:
или
).

Решение . Действительно, так как , то для любых элементов x , y A имеем:
,
, где
,
. Тогда

Так как , то
, поэтому
.

Проверим выполнимость второго условия теоремы. Если x – любой вектор из A и t – любое число из P , то . Поскольку
и
,, то
, , поэтому
. Таким образом, согласно теореме , множество A – подпространство линейного пространства L .

Для конечномерных линейных пространств справедливо и обратное утверждение.

Теорема. Всякое подпространство А линейного пространства L над полем является линейной оболочкой некоторой системы векторов.

При решении задачи нахождения базиса и размерности линейной оболочки используют следующую теорему.

Теорема. Базис линейной оболочки
совпадает с базисом системы векторов . Размерность линейной оболочки совпадает с рангом системы векторов .

Пример 4. Найти базис и размерность подпространства
линейного пространства Р 3 [ x ] , если
,
,
,
.

Решение . Известно, что векторы и их координатные строки (столбцы) обладают одинаковыми свойствами (в отношении линейной зависимости). Составляем матрицу A =
из координатных столбцов векторов
в базисе
.

Найдем ранг матрицы A .

. М 3 =
.
.

Следовательно, ранг r (A )= 3. Итак, ранг системы векторов равен 3. Значит, размерность подпространства S равна 3, а его базис состоит из трех векторов
(т.к. в базисный минор
входят координаты только этих векторов).

Пример 5. Доказать, что множество H векторов арифметического пространства
, у которых первая и последняя координаты равны 0, составляет линейное подпространство. Найти его базис и размерность.

Решение . Пусть
.

Тогда , и . Следовательно,
для любых . Если
,
, то . Таким образом, согласно теореме о линейном подпространстве, множество H является линейным подпространством пространства . Найдем базис H . Рассмотрим следующие векторы из H :
,
, . Эта система векторов линейно независима. Действительно, пусть .

Подмножество линейного пространства образует подпространство, если оно замкнуто относительно сложения векторов и умножения на скаляры.

П р и м е р 6.1. Образует ли подпространство в плоскости множество векторов, концы которых лежат: а) в первой четверти; б) на прямой, проходящей через начало координат? (начала векторов лежат в начале координат)

а) нет, так как множество не замкнуто относительно умножения на скаляр: при умножении на отрицательное число конец вектора попадает в третью четверть.

б) да, так как при сложении векторов и умножении их на любое число их концы остаются на той же прямой.

У п р а ж н е н и е 6.1. Образуют ли подпространство следующие подмножества соответствующих линейных пространств:

а) множество векторов плоскости, концы которых лежат в первой или третьей четверти;

б) множество векторов плоскости, концы которых лежат на прямой, не проходящей через начало координат;

в) множество координатных строк ;

г) множество координатных строк ;

д) множество координатных строк .

Размерностью линейного пространства L называется число dim L векторов, входящих в любой его базис.

Размерность суммы и пересечения подпространств связаны соотношением

dim (U + V) = dim U + dim V – dim (U Ç V).

П р и м е р 6.2. Найти базис и размерность суммы и пересечения подпространств, натянутых на следующие системы векторов:

Р е ш е н и е. Каждая из систем векторов, порождающих подпространства U и V, линейно независима, значит, является базисом соответствующего подпространства. Построим матрицу из координат данных векторов, расположив их по столбцам и отделив чертой одну систему от другой. Приведем получившуюся матрицу к ступенчатому виду.

Базис U + V образуют векторы , , , которым в ступенчатой матрице соответствуют ведущие элементы. Следовательно, dim (U + V) = 3. Тогда

dim (UÇV) = dim U + dim V – dim (U + V) = 2 + 2 – 3 = 1.

Пересечение подпространств образует множество векторов, удовлетворяющих уравнению (стоящих в левой и правой частях этого уравнения). Базис пересечения получим с помощью фундаментальной системы решений системы линейных уравнений, соответствующей этому векторному уравнению. Матрица этой системы уже приведена к ступенчатому виду. Исходя из него, заключаем, что y 2 – свободная переменная, и полагаем y 2 = c. Тогда 0 = y 1 – y 2 , y 1 = c,. и пересечение подпространств образует множество векторов вида = с (3, 6, 3, 4). Следовательно, базис UÇV образует вектор (3, 6, 3, 4).

З а м е ч а н и я. 1. Если продолжить решать систему, находя значения переменных х, то получим x 2 = c, x 1 = c, и в левой части векторного уравнения получится вектор , равный полученному выше.

2. Указанным методом можно получить базис суммы независимо от того, являются ли порождающие системы векторов линейно независимыми. Но базис пересечения будет получен правильно, только если хотя бы система, порождающая второе подпространство, линейно независима.

3. Если будет установлено, что размерность пересечения равна 0, то пересечение не имеет базиса, и искать его не нужно.

У п р а ж н е н и е 6.2. Найти базис и размерность суммы и пересечения подпространств, натянутых на следующие системы векторов:

а)

б)

Евклидовым пространством называется линейное пространство над полем R , в котором определено скалярное умножение, ставящее в соответствие каждой паре векторов , скаляр , причем выполнены условия:

Стандартное скалярное произведение вычисляется по формулам

(a 1 , … , a n) (b 1 , … , b n) = a 1 b 1 + … + a n b n .

Векторы и называются ортогональными, записывается ^ , если их скалярное произведение равно 0.

Система векторов называется ортогональной, если векторы в ней попарно ортогональны.

Ортогональная система векторов линейно независима.

Процесс ортогонализации системы векторов , … , заключается в переходе к эквивалентной ортогональной системе , … , , выполняемом по формулам:

, где , k = 2, … , n.

П р и м е р 7.1. Ортогонализировать систему векторов

= (1, 2, 2, 1), = (3, 2, 1, 1), = (4, 1, 3, -2).

Р е ш е н и е. Имеем = = (1, 2, 2, 1);

, = = = 1;

= (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0).

, = = =1;

= =1;

= (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).

У п р а ж н е н и е 7.1. Ортогонализировать системы векторов:

а) = (1, 1, 0, 2), = (3, 1, 1, 1), = (-1, -3, 1, -1);

б) = (1, 2, 1, 1), = (3, 4, 1, 1), = (0, 3, 2, -1).

П р и м е р 7.2. Дополнить систему векторов = (1, -1, 1, -1),

= (1, 1, -1, -1), до ортогонального базиса пространства.

Р е ш е н и е. Исходная система ортогональна, поэтому задача имеет смысл. Так как векторы заданы в четырехмерном пространстве, то требуется найти еще два вектора. Третий вектор = (x 1 , x 2 , x 3 , x 4) определяем из условий = 0, = 0. Эти условия дают систему уравнений, матрица которой образована из координатных строк векторов и . Решаем систему:

Свободным переменным x 3 и x 4 можно придать любой набор значений, отличный от нулевого. Полагаем, например, x 3 = 0, x 4 = 1. Тогда x 2 = 0, x 1 = 1, и = (1, 0, 0, 1).

Аналогично находим = (y 1 , y 2 , y 3 , y 4). Для этого к полученной выше ступенчатой матрице добавляем новую координатную строку и приводим к ступенчатому виду:

Для свободной переменной y 3 полагаем y 3 = 1. Тогда y 4 = 0, y 2 = 1, y 1 = 0, и = (0, 1, 1, 0).

Нормой вектора евклидова пространства называется неотрицательное действительное число .

Вектор называется нормированным, если его норма равна 1.

Чтобы нормировать вектор, его следует разделить на его норму.

Ортогональная система нормированных векторов называется ортонормированной.

У п р а ж н е н и е 7.2. Дополнить систему векторов до ортонормированного базиса пространства:

а) = (1/2, 1/2, 1/2, 1/2), = (-1/2, 1/2, -1/2, 1/2);

Пусть U и V – линейные пространства над полем F. Отображение f: U ® V называется линейным, если и .

П р и м е р 8.1. Являются ли линейными преобразования трехмерного пространства:

а) f(x 1 , x 2 , x 3) = (2x 1 , x 1 – x 3 , 0);

б) f(x 1 , x 2 , x 3) = (1, x 1 + x 2 , x 3).

а) Имеем f((x 1 , x 2 , x 3) + (y 1 , y 2 , y 3)) = f(x 1 + y 1 , x 2 + y 2 , x 3 + y 3) =

= (2(x 1 + y 1), (x 1 + y 1) – (x 3 + y 3), 0) = (2x 1 , x 1 – x 3 , 0) + (2y 1 , y 1 — y 3 , 0) =

F((x 1 , x 2 , x 3) + f(y 1 , y 2 , y 3));

f(l(x 1 , x 2 , x 3)) = f(lx 1 , lx 2 , lx 3) = (2lx 1 , lx 1 – lx 3 , 0) = l(2x 1 , x 1 – x 3 , 0) =

L f(x 1 , x 2 , x 3).

Следовательно, преобразование является линейным.

б) Имеем f((x 1 , x 2 , x 3) + (y 1 , y 2 , y 3)) = f(x 1 + y 1 , x 2 + y 2 , x 3 + y 3) =

= (1, (x 1 + y 1) + (x 2 + y 2), x 3 + y 3);

f((x 1 , x 2 , x 3) + f(y 1 , y 2 , y 3)) = (1, x 1 + x 2 , x 3) + (1, y 1 + y 2 , y 3) =

= (2, (x 1 + y 1) + (x 2 + y 2), x 3 + y 3) ¹ f((x 1 , x 2 , x 3) + (y 1 , y 2 , y 3)).

Следовательно, преобразование не является линейным.

Образом линейного отображения f: U ® V называется множество образов векторов из U, то есть

У п р а ж н е н и е 8.1. Найти ранг, дефект, базисы образа и ядра линейного отображения f, заданного матрицей:

а) А = ; б) А = ; в) А = .

Когда мы разбирали понятия n -мерного вектора и вводили операции над векторами, то выяснили, что множество всех n -мерных векторов порождает линейное пространство. В этой статье мы поговорим о важнейших связанных понятиях – о размерности и базисе векторного пространства. Также рассмотрим теорему о разложении произвольного вектора по базису и связь между различными базисами n -мерного пространства. Подробно разберем решения характерных примеров.

Навигация по странице.

Видео:Базисные решения систем линейных уравнений (03)Скачать

Понятие размерности векторного пространства и базиса.

Понятия размерности и базиса векторного пространства напрямую связаны с понятием линейно независимой системы векторов, так что рекомендуем при необходимости обращаться к статье линейная зависимость системы векторов, свойства линейной зависимости и независимости.

Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Приведем некоторые рассуждения, основываясь на этих определениях.

Рассмотрим пространство n -мерных векторов.

Покажем, что размерность этого пространства равна n .

Возьмем систему из n единичных векторов вида

Примем эти векторы в качестве строк матрицы А . В этом случае матрица А будет единичной матрицей размерности n на n . Ранг этой матрицы равен n (при необходимости смотрите статью ). Следовательно, система векторов линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы являются базисом этого пространства .

Из последнего утверждения и определения базиса можно сделать вывод, что любая система n -мерных векторов, число векторов в которой меньше n , не является базисом .

Теперь переставим местами первый и второй вектор системы . Легко показать, что полученная система векторов также является базисом n -мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n . Таким образом, система из n векторов линейно независима и является базисом n -мерного векторного пространства.

Если переставить местами другие векторы системы , то получим еще один базис.

Если взять линейно независимую систему не единичных векторов, то она также является базисом n -мерного векторного пространства.

Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n -мерных векторов.

Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.

Рассмотрим несколько примеров.

Являются ли векторы базисом трехмерного векторного пространства?

Исследуем эту систему векторов на линейную зависимость. Для этого составим матрицу, строками которой будут координаты векторов, и найдем ее ранг:

Таким образом, векторы a , b и c линейно независимы и их количество равно размерности векторного пространства, следовательно, они являются базисом этого пространства.

Может ли система векторов быть базисом векторного пространства?

Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема исходной системы векторов является базисом).

Убедитесь, что векторы

могут быть базисом четырехмерного векторного пространства.

Составим матрицу, приняв ее строками исходные векторы:

Найдем :

Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.

Исходные векторы действительно являются базисом четырехмерного пространства.

Составляют ли векторы базис векторного пространства размерности 4 ?

Даже если исходная система векторов линейно независима, количество векторов в ней недостаточно для того, чтобы быть базисом четырехмерного пространства (базис такого пространства состоит из 4 векторов).

Нет, не составляет.

Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Разложение вектора по базису векторного пространства.

Пусть произвольные векторы являются базисом n -мерного векторного пространства. Если к ним добавить некоторый n -мерный вектор x , то полученная система векторов будет линейно зависимой. Из свойств линейной зависимости мы знаем, что хотя бы один вектор линейно зависимой системы линейно выражается через остальные. Иными словами, хотя бы один из векторов линейно зависимой системы раскладывается по остальным векторам.

Так мы подошли к очень важной теореме.

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Пусть — базис n -мерного векторного пространства. Добавим к этим векторам n -мерный вектор x . Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где — некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.

Предположим, что существует еще одно разложение , где — некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :

Так как система базисных векторов линейно независима, то по определению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты равны нулю. Поэтому, , что доказывает единственность разложения вектора по базису.

Коэффициенты называются координатами вектора x в базисе .

После знакомства с теоремой о разложении вектора по базису, мы начинаем понимать суть выражения «нам задан n -мерный вектор ». Это выражение означает, что мы рассматриваем вектор x n -мерного векторного пространства, координаты которого заданы в некотором базисе. При этом мы понимаем, что этот же вектор x в другом базисе n-мерного векторного пространства будет иметь координаты, отличные от .

Рассмотрим следующую задачу.

Пусть в некотором базисе n -мерного векторного пространства нам задана система из n линейно независимых векторов

и вектор . Тогда векторы также являются базисом этого векторного пространства.

Пусть нам требуется найти координаты вектора x в базисе . Обозначим эти координаты как .

Вектор x в базисе имеет представление . Запишем это равенство в координатной форме:

Это равенство равносильно системе из n линейных алгебраических уравнений с n неизвестными переменными :

Основная матрица этой системы имеет вид

Обозначим ее буквой А . Столбцы матрицы А представляют собой векторы линейно независимой системы векторов , поэтому ранг этой матрицы равен n , следовательно, ее определитель отличен от нуля. Этот факт указывает на то, что система уравнений имеет единственное решение, которое может быть найдено любым методом, например, или .

Так будут найдены искомые координаты вектора x в базисе .

Разберем теорию на примерах.

В некотором базисе трехмерного векторного пространства заданы векторы

Убедитесь, что система векторов также является базисом этого пространства и найдите координаты вектора x в этом базисе.

Чтобы система векторов была базисом трехмерного векторного пространства нужно, чтобы она была линейно независима. Выясним это, определив ранг матрицы A , строками которой являются векторы . Ранг найдем методом Гаусса

следовательно, Rank(A) = 3 , что показывает линейную независимость системы векторов .

Итак, векторы являются базисом. Пусть в этом базисе вектор x имеет координаты . Тогда, как мы показали выше, связь координат этого вектора задается системой уравнений

Подставив в нее известные из условия значения, получим

Решим ее методом Крамера:

Таким образом, вектор x в базисе имеет координаты .

В некотором базисе четырехмерного векторного пространства задана линейно независимая система векторов

Известно, что . Найдите координаты вектора x в базисе .

Так как система векторов линейно независима по условию, то она является базисом четырехмерного пространства. Тогда равенство означает, что вектор x в базисе имеет координаты . Обозначим координаты вектора x в базисе как .

Система уравнений, задающая связь координат вектора x в базисах и имеет вид

Подставляем в нее известные значения и находим искомые координаты :

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Связь между базисами.

Пусть в некотором базисе n -мерного векторного пространства заданы две линейно независимые системы векторов

и

то есть, они тоже являются базисами этого пространства.

Если — координаты вектора в базисе , то связь координат и задается системой линейных уравнений (об этом мы говорили в предыдущем пункте):

, которая в матричной форме может быть записана как

Аналогично для вектора мы можем записать

Предыдущие матричные равенства можно объединить в одно, которое по сути задает связь векторов двух различных базисов

Аналогично мы можем выразить все векторы базиса через базис :

Матрицу называют матрицей перехода от базиса к базису , тогда справедливо равенство

Умножив обе части этого равенства справа на

получим

Найдем матрицу перехода, при этом не будем подробно останавливаться на нахождении обратной матрицы и умножении матриц (смотрите при необходимости статьи и ):

Осталось выяснить связь координат вектора x в заданных базисах.

Пусть в базисе вектор x имеет координаты , тогда

а в базисе вектор x имеет координаты , тогда

Так как левые части последних двух равенств одинаковы, то мы можем приравнять правые части:

Если умножить обе части справа на

С другой стороны

(найдите обратную матрицу самостоятельно).
Два последних равенства дают нам искомую связь координат вектора x в базисах и .

Матрица перехода от базиса к базису имеет вид
;
координаты вектора x в базисах и связаны соотношениями

или
.

Мы рассмотрели понятия размерности и базиса векторного пространства, научились раскладывать вектор по базису и обнаружили связь между разными базисами n-мерного пространства векторов через матрицу перехода.

Линейное пространство V называется n-мерным , если в нем существует система из n линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число n называется размерностью (числом измерений) линейного пространства V и обозначается operatornameV . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве V найдется система, состоящая из n линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: operatornameV=infty ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.

Базисом n-мерного линейного пространства называется упорядоченная совокупность n линейно независимых векторов ( базисных векторов ).

Теорема 8.1 о разложении вектора по базису. Если — базис n-мерного линейного пространства V , то любой вектор mathbfin V может быть представлен в виде линейной комбинации базисных векторов:

mathbf=mathbf_1cdot mathbf_1+mathbf_2cdot mathbf_2+ldots+mathbf_ncdot mathbf_n

и притом единственным образом, т.е. коэффициенты mathbf_1, mathbf_2,ldots, mathbf_n определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.

Действительно, размерность пространства V равна n . Система векторов mathbf_1,mathbf_2,ldots,mathbf_n линейно независима (это базис). После присоединения к базису любого вектора mathbf , получаем линейно зависимую систему mathbf_1,mathbf_2,ldots,mathbf_n, mathbf (так как это система состоит из (n+1) векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.

Следствие 1. Если mathbf_1,mathbf_2,ldots,mathbf_n — базис пространства V , то V=operatorname (mathbf_1,mathbf_2, ldots,mathbf_n) , т.е. линейное пространство является линейной оболочкой базисных векторов.

В самом деле, для доказательства равенства V=operatorname (mathbf_1,mathbf_2, ldots, mathbf_n) двух множеств достаточно показать, что включения Vsubset operatorname(mathbf_1,mathbf_2, ldots,mathbf_n) и выполняются одновременно. Действительно, с одной стороны, любая линейная комбинация векторов линейного пространства принадлежит самому линейному пространству, т.е. operatorname(mathbf_1,mathbf_2,ldots,mathbf_n)subset V . С другой стороны, любой вектор пространства по теореме 8.1 можно представить в виде линейной комбинации базисных векторов, т.е. Vsubset operatorname(mathbf_1,mathbf_2,ldots,mathbf_n) . Отсюда следует равенство рассматриваемых множеств.

Следствие 2. Если mathbf_1,mathbf_2,ldots,mathbf_n — линейно независимая система векторов линейного пространства V и любой вектор mathbfin V может быть представлен в виде линейной комбинации (8.4): mathbf=v_1mathbf_1+ v_2mathbf_2+ldots+v_nmathbf_n , то пространство V имеет размерность n , а система mathbf_1,mathbf_2, ldots,mathbf_n является его базисом.

В самом деле, в пространстве V имеется система n линейно независимых векторов, а любая система mathbf_1,mathbf_2,ldots,mathbf_n из большего количества векторов (k>n) линейно зависима, поскольку каждый вектор из этой системы линейно выражается через векторы mathbf_1,mathbf_2,ldots,mathbf_n . Значит, operatorname V=n и mathbf_1,mathbf_2,ldots,mathbf_n — базис V .

Теорема 8.2 о дополнении системы векторов до базиса. Всякую линейно независимую систему k векторов n-мерного линейного пространства (1leqslant k V

(1leqslant k . Рассмотрим линейную оболочку этих векторов: L_k=operatorname(mathbf_1,mathbf_2,ldots, mathbf_k) . Любой вектор mathbfin L_k образует с векторами mathbf_1,mathbf_2,ldots, mathbf_k линейно зависимую систему mathbf_1,mathbf_2,ldots,mathbf_k,mathbf , так как вектор mathbf линейно выражается через остальные. Поскольку в n-мерном пространстве существует n линейно независимых векторов, то L_kne V и существует вектор mathbf_in V , который не принадлежит L_k . Дополняя этим вектором линейно независимую систему mathbf_1,mathbf_2,ldots,mathbf_k , получаем систему векторов mathbf_1,mathbf_2,ldots,mathbf_k,mathbf_ , которая также линейно независимая. Действительно, если бы она оказалась линейно зависимой, то из пункта 1 замечаний 8.3 следовало, что mathbf_in operatorname(mathbf_1, mathbf_2, ldots,mathbf_k)=L_k , а это противоречит условию mathbf_notin L_k . Итак, система векторов mathbf_1,mathbf_2,ldots, mathbf_k, mathbf_ линейно независимая. Значит, первоначальную систему векторов удалось дополнить одним вектором без нарушения линейной независимости. Продолжаем аналогично. Рассмотрим линейную оболочку этих векторов: L_=operatorname (mathbf_1, mathbf_2,ldots, mathbf_k, mathbf_) . Если L_=V , то mathbf_1,mathbf_2, ldots,mathbf_k, mathbf_ — базис и теорема доказана. Если L_ne V , то дополняем систему mathbf_1,mathbf_2, ldots,mathbf_k,mathbf_ вектором mathbf_notin L_ и т.д. Процесс дополнения обязательно закончится, так как пространство V конечномерное. В результате получим равенство V=L_n=operatorname (mathbf_1,ldots,mathbf_k,ldots,mathbf_n) , из которого следует, что mathbf_1,ldots,mathbf_k,ldots,mathbf_n — базис пространства V . Теорема доказана.

1. Базис линейного пространства определяется неоднозначно. Например, если mathbf_1,mathbf_2, ldots, mathbf_n — базис пространства V , то система векторов lambda mathbf_1,lambda mathbf_2,ldots,lambda mathbf_n при любом lambdane0 также является базисом V . Количество базисных векторов в разных базисах одного и того же конечномерного пространства, разумеется, одно и то же, так как это количество равно размерности пространства.

2. В некоторых пространствах, часто встречающихся в приложениях, один из возможных базисов, наиболее удобный с практической точки зрения, называют стандартным.

3. Теорема 8.1 позволяет говорить, что базис — это полная система элементов линейного пространства, в том смысле, что любой вектор пространства линейно выражается через базисные векторы.

4. Если множество mathbb является линейной оболочкой operatorname(mathbf_1,mathbf_2,ldots,mathbf_k) , то векторы mathbf_1,mathbf_2,ldots,mathbf_k называют образующими множества mathbb . Следствие 1 теоремы 8.1 в силу равенства V=operatorname (mathbf_1,mathbf_2,ldots,mathbf_n) позволяет говорить, что базис — это минимальная система образующих линейного пространства V , так как нельзя уменьшить количество образующих (удалить хотя бы один вектор из набора mathbf_1, mathbf_2,ldots,mathbf_n ) без нарушения равенства V=operatorname(mathbf_1,mathbf_2,ldots,mathbf_n) .

5. Теорема 8.2 позволяет говорить, что базис — это максимальная линейно независимая система векторов линейного пространства, так как базис — это линейно независимая система векторов, и ее нельзя дополнить каким-либо вектором без потери линейной независимости.

6. Следствие 2 теоремы 8.1 удобно применять для нахождения базиса и размерности линейного пространства. В некоторых учебниках оно берется за определение базиса, а именно: линейно независимая система mathbf_1,mathbf_2,ldots,mathbf_n векторов линейного пространства называется базисом, если любой вектор пространства линейно выражается через векторы mathbf_1,mathbf_2,ldots,mathbf_n . Количество базисных векторов определяет размерность пространства . Разумеется, что эти определения эквивалентны приведенным выше.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Примеры базисов линейных пространств

Укажем размерность и базис для примеров линейных пространств, рассмотренных выше.

1. Нулевое линейное пространство <mathbf> не содержит линейно независимых векторов. Поэтому размерность этого пространства полагают равной нулю: dim<mathbf>=0 . Это пространство не имеет базиса.

2. Пространства V_1,,V_2,,V_3 имеют размерности 1, 2, 3 соответственно. Действительно, любой ненулевой вектор пространства V_1 , образует линейно независимую систему (см. пункт 1. замечаний 8.2), а любые два ненулевых век тора пространства V_1 коллинеарны, т.е. линейно зависимы (см. пример 8.1). Следовательно, dim=1 , а базисом пространства V_1 является любой ненулевой вектор. Аналогично доказывается, что dim=2 и dim=3 . Базисом пространства V_2 служат любые два неколлинеарных вектора, взятые в определенном порядке (один из них считается первым базисным вектором, другой — вторым). Базисом пространства V_3 являются любые три некомпланарных (не лежащих в одной или параллельных плоскостях) вектора, взятые в определенном порядке. Стандартным базисом в V_1 является единичный вектор vec на прямой. Стандартным базисом в V_2 считается базис vec,,vec , со стоящий из двух взаимно перпендикулярных единичных векторов плоскости. Стандартным базисом в пространстве V_3 считается базис vec,,vec,,vec , составленный из трех единичных попарно перпендикулярных векторов, образующих правую тройку.

3. Пространство mathbb^n содержит не более, чем n , линейно независимых векторов. В самом деле, возьмем k столбцов из mathbb^n и составим из них матрицу размеров ntimes k . Если k>n , то столбцы линейно зависимы по теореме 3.4 о ранге матрицы. Следовательно, dim<mathbb^n>leqslant n . В пространстве mathbb^n не трудно найти п линейно независимых столбцов. Например, столбцы единичной матрицы

линейно независимы. Следовательно, dim<mathbb^n>=n . Пространство mathbb^n называется n-мерным вещественным арифметическим пространством . Указанный набор векторов считается стандартным базисом пространства mathbb^n . Аналогично доказывается, что dim<mathbb^n>=n , поэтому пространство mathbb^n называют n-мерным комплексным арифметическим пространством .

4. Напомним, что любое решение однородной системы Ax=o можно представить в виде x=C_1varphi_1+C_2varphi_2+ldots+C_varphi_ , где r=operatornameA , a varphi_1,varphi_2,ldots,varphi_ — фундаментальная система решений. Следовательно, =operatorname (varphi_1,varphi_2,ldots,varphi_) , т.е. базисом пространства решений однородной системы служит ее фундаментальная система решений, а размерность пространства dim=n-r , где n — количество неизвестных, а r — ранг матрицы системы.

5. В пространстве M_ матриц размеров 2times3 можно выбрать 6 матриц:

которые линейно независимы. Действительно, их линейная комбинация

alpha_1cdot mathbf_1+alpha_2cdot mathbf_2+alpha_3cdot mathbf_3+ alpha_4cdot mathbf_4+alpha_5cdot mathbf_5+alpha_6cdot mathbf_6= beginalpha_1&alpha_2&alpha_3\ alpha_4&alpha_5&alpha_6end

равна нулевой матрице только в тривиальном случае alpha_1=alpha_2= ldots= alpha_6=0 . Прочитав равенство (8.5) справа налево, заключаем, что любая матрица из M_ линейным образом выражается через выбранные 6 матриц, т.е. M_= operatorname (mathbf_1,mathbf_2,ldots,mathbf_6) . Следовательно, dim<M_>=2cdot3=6 , а матрицы mathbf_1, mathbf_2,ldots,mathbf_6 являются базисом (стандартным) этого пространства. Аналогично доказывается, что dim<M_>=mcdot n .

6. Для любого натурального n в пространстве P(mathbb) многочленов с комплексными коэффициентами можно найти п линейно независимых элементов. Например, многочлены mathbf_1=1, mathbf_2=z, mathbf_3=z^2,,ldots, mathbf_n=z^ линейно независимы, так как их линейная комбинация

a_1cdot mathbf_1+a_2cdot mathbf_2+ldots+a_ncdot mathbf_n= a_1+a_2z+ldots+a_nz^

равна нулевому многочлену (o(z)equiv0) только в тривиальном случае a_1=a_2=ldots=a_n=0 . Поскольку эта система многочленов линейно независима при любом натуральном л, пространство P(mathbb) бесконечномерное. Аналогично делаем вывод о бесконечной размерности пространства P(mathbb) многочленов с действительными коэффициентами. Пространство P_n(mathbb) многочленов степени не выше, чем n , конечномерное. Действительно, векторы mathbf_1=1, mathbf_2=x, mathbf_3=x^2,,ldots, mathbf_=x^n образуют базис (стандартный) это го пространства, так как они линейно независимы и любой многочлен из P_n(mathbb) можно представить в виде линейной комбинации этих векторов:

a_nx^n+ldots+a_1x+a_0=a_0cdot mathbf_1+a_1 mathbf_2+ldots+a_ncdot mathbf_ . Следовательно, dim<P_n(mathbb)>=n+1 .

7. Пространство C(mathbb) непрерывных функций является бесконечно мерным. Действительно, для любого натурального n многочлены 1,x,x^2,ldots, x^ , рассматриваемые как непрерывные функции, образуют линейно независимые системы (см. предыдущий пример).

В пространстве T_(mathbb) тригонометрических двучленов (частоты omegane0 ) с действительными коэффициентами базис образуют одночлены mathbf_1(t)=sinomega t,

mathbf_2(t)=cosomega t . Они линейно независимы, так как тождественное равенство asinomega t+bcosomega tequiv0 возможно только в тривиальном случае (a=b=0) . Любая функция вида f(t)=asinomega t+bcosomega t линейно выражается через базисные: f(t)=a,mathbf_1(t)+b,mathbf_2(t) .

8. Пространство mathbb^X действительных функций, определенных на множестве X , в зависимости от области определения X может быть конечномерным или бесконечномерным. Если X — конечное множество, то пространство mathbb^X конечномерное (например, X= ). Если X — бесконечное множество, то пространство mathbb^X бесконечномерное (например, пространство mathbb^N последовательностей).

9. В пространстве mathbb^ любое положительное число mathbf_1 , не равное единице, может служить базисом. Возьмем, например, число mathbf_1=2 . Любое положительное число r можно выразить через mathbf_1 , т.е. представить в виде alphacdot mathbf_1colon r=2^=log_2rast2=alpha_1ast mathbf_1 , где alpha_1=log_2r . Следовательно, размерность этого пространства равна 1, а число mathbf_1=2 является базисом.

10. Пусть mathbf_1,mathbf_2,ldots,mathbf_n — базис вещественного линейного пространства V . Определим на V линейные скалярные функции , положив:

mathcal_i(mathbf_j)=begin1,&i=j,\ 0,&ine j.end

При этом, в силу линейности функции mathcal_i , для произвольного вектора получаем mathcal(mathbf)=sum_^v_j mathcal(mathbf_j)=v_i .

Итак, определены n элементов (ковекторов) mathcal_1, mathcal_2, ldots, mathcal_n сопряженного пространства V^ . Докажем, что mathcal_1, mathcal_2,ldots, mathcal_n — базис V^ .

Во-первых, покажем, что система mathcal_1, mathcal_2,ldots, mathcal_n линейно независима. В самом деле, возьмем линейную комбинацию этих ковекторов (alpha_1 mathcal_1+ldots+alpha_nmathcal_n)(mathbf)= и приравняем ее нулевой функции

forall mathbfin V)colon

forall mathbfin V.

Подставляя в это равенство mathbf=mathbf_i,

i=1,ldots,n , получаем alpha_1=alpha_2cdot= alpha_n=0 . Следовательно, система элементов mathcal_1,mathcal_2,ldots,mathcal_n пространства V^ линейно независима, так как равенство alpha_1mathcal_1+ldots+ alpha_nmathcal_n =mathbf возможно только в тривиальном случае.

Во-вторых, докажем, что любую линейную функцию fin V^ можно представить в виде линейной комбинации ковекторов mathcal_1, mathcal_2,ldots, mathcal_n . Действительно, для любого вектора mathbf=v_1 mathbf_1+v_2 mathbf_2+ldots+v_n mathbf_n в силу линейности функции f получаем:

beginf(mathbf)&= f(v_1 mathbf_1+ldots+v_n mathbf_n)= v_1 f(mathbf_1)+ldots+v_n f(mathbf_n)= f(mathbf_1)mathcal_1(mathbf)+ ldots+ f(mathbf_n)mathcal_n(mathbf)=\ &=(f(mathbf_1)mathcal_1+ldots+ f(mathbf_n)mathcal_n)(mathbf)= (beta_1mathcal_1+ ldots+beta_nmathcal_n) (mathbf),end

т.е. функция f представлена в виде линейной комбинации f=beta_1 mathcal_1+ldots+beta_nmathcal_n функций mathcal_1,mathcal_2,ldots, mathcal_n (числа beta_i=f(mathbf_i) — коэффициенты линейной комбинации). Следовательно, система ковекторов mathcal_1, mathcal_2,ldots, mathcal_n является базисом сопряженного пространства V^ и dim<V^>=dim (для конечномерного пространства V ).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.