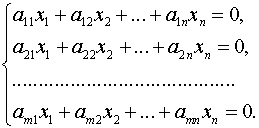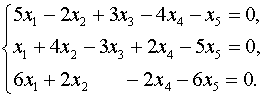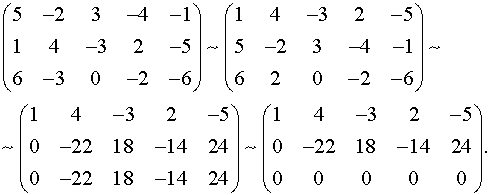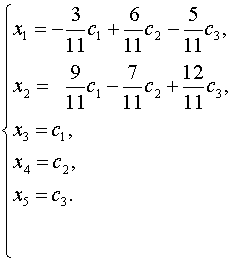Найти размерность и базис подпространства заданного системой линейных уравнений (5 видео)

Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3

Содержание

Системы линейных однородных уравнений
Примеры решений. Линейные пространства
Решения задач: линейные пространства
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Линейное пространство
Определения
Примеры линейных пространств
Изоморфизм
Линейная зависимость, базис, координаты
Критерии линейной зависимости
Относительный базис
Сумма и пересечение линейных подпространств
Прямая сумма линейных подпространств
Линейные многообразия
🎥 Видео

Системы линейных однородных уравнений

Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы

1. Записываем матрицу системы:

и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:

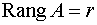
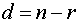
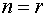
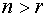
Размерность пространства решений равна . Если , то однородная система имеет единственное нулевое решение, если , то система имеет бесчисленное множество решений.

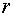
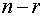
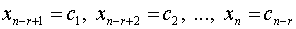
2. Выбираем базисных и свободных переменных. Свободные переменные обозначаем . Затем базисные переменные выражаем через свободные, получив таким образом общее решение однородной системы линейных уравнений.

3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.

Примечание. К элементарным преобразованиям матрицы относят:

1. умножение (деление) строки на множитель, отличный от нуля;

2. прибавление к какой-либо строке другой строки, умноженной на любое число;

3. перестановка строк местами;

4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).

Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.

Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:

Полагаем , тогда

Размерность линейного пространства решений равна 3.

:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Примеры решений. Линейные пространства

В этом разделе вы найдете бесплатные решения задач о линейных пространствах по темам: проверка линейности подпространства, базис пространства и подпространства, ортогональное подпространство, размерность.

Видео:Линейная оболочка. Базис и размерностьСкачать

Решения задач: линейные пространства

Задача 1. Образует ли линейное подпространство пространства $R^4$ множество $V$, заданное по правилу:

Задача 2. Даны векторы $e_1, e_2, e_3, e_4$ и $a$ в стандартном базисе пространства $R^4$.
Требуется:
а) убедиться, что векторы $e_1, e_2, e_3, e_4$ образуют базис пространства $R^4$;
б) найти разложение вектора $a$ по этому базису;
в) найти угол между векторами $e_1$ и $e_2$.

Задача 3.Найти ортогональный базис подпространства $L$, заданного системой уравнений, и базис подпространства $L^$

Задача 4. Для каждого из следующих множеств геометрических векторов определить, будет ли это множество линейным подпространством пространства $V_3$ :
1) радиус-векторы точек данной плоскости;
2) векторы, образующие с данным ненулевым вектором $overline$ угол $alpha$;
3) множество векторов, удовлетворяющих условию $|overline|=1$ .

Задача 5. Пусть $L$ — множество многочленов степени не выше 2, удовлетворяющих условию $p(1)+p'(1)+p»(1)=0$. Доказать, что $L$ — линейное подпространство в пространстве $P_2$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Задача 6. Образуют ли многочлены $p_1(x)=x^3+x^2-1$, $p_2(x)=x^2-2x$, $p_3(x)=x^3+x$, $p_4(x)=x^2-3$ базис в пространстве $P_3$?

Задача 7. Доказать, что матрицы вида $$ begin 2a & a+3b-2c\ b & 5c\ end $$ образуют линейное подпространство в пространстве матриц $M_$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

VMath

Инструменты сайта

Основное

Информация

Действия

Содержание

Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Линейное пространство

Видео:Базис линейного пространства (01)Скачать

Определения

Пусть дано множество $ mathbb V_=left $ элементов произвольной природы. Пусть для элементов этого множества определены две операции: сложения $ X+Y_ $ и умножения на любое вещественное число $ alpha_ $: $ alpha cdot X_ $, и множество $ mathbb V_ $ замкнуто относительно этих операций: $ X+Y in mathbb V , alpha cdot X in mathbb V_ $. Пусть эти операции подчиняются аксиомам:

1. $ X+Y=Y+X_ $ для $ subset mathbb V_ $;

2. $ (X+Y)+Z_=X+(Y+Z) $ для $ subset mathbb V_ $;

3. в $ mathbb V_ $ cуществует нулевой вектор $ mathbb O_ $ со свойством $ X+ mathbb O =X_ $ для $ forall Xin mathbb V_ $;

4. для каждого $ Xin mathbb V_ $ существует обратный вектор $ X^in mathbb V_ $ со свойством $ X+X^=mathbb O_ $;

5. $ 1cdot X=X_ $ для $ forall Xin mathbb V_ $;

6. $ lambda left(mu X right)_= left(lambda mu right)X $ для $ forall Xin mathbb V_ $, $ subset mathbb R_ $ ;

7. $ (lambda + mu)X=lambda X + mu X_ $ для $ forall Xin mathbb V_ $, $ subset mathbb R_ $ ;

8. $ lambda (X + Y) =lambda X_ + lambda Y $ для $ subset mathbb V_ , lambda in mathbb R $.

Тогда такое множество $ mathbb V_ $ называется линейным (векторным) пространством, его элементы называются векторами, и — чтобы подчеркнуть их отличие от чисел из $ mathbb R_ $ — последние называются скалярами 1) . Пространство, состоящее из одного только нулевого вектора, называется тривиальным .

Элементарно доказывается единственность нулевого вектора, и единственность вектора, обратного вектору $ Xin mathbb V_ $: $ X^=-1cdot X_ $, его привычно обозначают $ — X_ $.

Подмножество $ mathbb V_ $ линейного пространства $ mathbb V_ $, само являющееся линейным пространством (т.е. $ mathbb V_ $ замкнуто относительно сложения векторов и умножения на произвольный скаляр), называется линейным подпространством пространства $ mathbb V_ $. Тривиальными подпространствами линейного пространства $ mathbb V_ $ называются само $ mathbb V_ $ и пространство, состоящее из одного нулевого вектора $ mathbb O_ $.

Видео:Базисные решения систем линейных уравнений (03)Скачать

Примеры линейных пространств

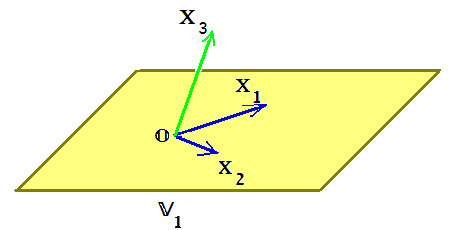
Пример 1. Пространство $ mathbb R^ $ упорядоченных троек вещественных чисел $ (a_1,a_2,a_) $ с операциями, определяемыми равенствами:

$$ (a_1,a_2,a_3)+(b_1,b_2,b_3)= (a_1+b_1,a_2+b_2,a_3+b_3), alpha (a_1,a_2,a_3) = ( alpha a_1, alpha a_2, alpha a_3 ) . $$ Геометрическая интерпретация очевидна: вектор в пространстве, «привязанный» к началу координат, может быть задан координатами своего конца $ (a_1,a_2,a_) $. На рисунке показано и типичное подпространство пространства $ mathbb R^ $: плоскость, проходящая через начало координат. 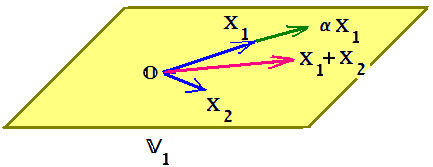Точнее говоря, элементами $ mathbb V_1 $ являются векторы, имеющие начало в начале координат и концы — в точках плоскости. Замкнутость такого множества относительно сложения векторов и их растяжения 2) очевидна.

Пример 2. Основываясь на том же примере, можно дать и иную интерпретацию векторного пространства $ mathbb V_1 $ (заложенную, кстати, уже в самом происхождении слова «вектор» 3) ) — оно определяет набор «сдвигов» точек пространства $ mathbb R^ $. Эти сдвиги — или параллельные переносы любой пространственной фигуры — выбираются параллельными плоскости $ mathbb V_1 $.

Пример 3. Естественным обобщением $ mathbb R^ $ служит пространство $ mathbb R_^ $: векторное пространство строк $ (x_1,dots,x_) $ или столбцов $ (x_1,dots,x_n)^ $. Один из способов задания подпространства в $ mathbb R_^ $ — задание набора ограничений. Множество решений системы линейных однородных уравнений:

$$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&0,\ a_x_1 +a_x_2+ldots+a_x_n &=&0,\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&0 endright. iff AX=mathbb O $$ образует линейное подпространство пространства $ mathbb R_^ $. В самом деле, если $$x_1=alpha_1,dots, x_n=alpha_n $$ — решение системы, то и $$x_1=t alpha_1,dots, x_n= t alpha_n $$ — тоже решение при любом $ t in mathbb R $. Если $$x_1=beta_1,dots, x_n=beta_n $$ — еще одно решение системы, то и $$x_1=alpha_1+beta_1,dots,x_n=alpha_n+beta_n $$ — тоже будет ее решением.

Почему множество решений системы неоднородных уравнений не образует линейного подпространства?

Пример 4. Обобщая далее, можем рассмотреть пространство «бесконечных» строк или последовательностей

$$ (x_1,dots,x_n, dots ) , , $$ обычно являющееся объектом математического анализа — при рассмотрении последовательностей и рядов. Подпространство этого пространства образуют, например, линейные рекуррентные последовательности $ _ $ удовлетворяющие — при произвольных числах $ <x_0,dots x_> subset mathbb R $ — линейному однородному разностному уравнению $ n_ $-го порядка, $$ x_=a_1 x_+ dots+ a_n x_K npu K in ; $$ здесь числа $ < a_1,dots,a_, a_n ne 0 > subset mathbb R $ считаются фиксированными.

Пример 5. Множество $ mtimes n_ $-матриц с вещественными элементами с операциями сложения матриц и умножения на вещественные числа образует линейное пространство. Будем обозначать это пространство $ mathbb R^ $.

В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.

Пример 6. Множество полиномов одной переменной $ x_ $ степени в точности равной $ n_ $ с коэффициентами из $ mathbb A_ $ (где $ mathbb A_ $ — любое из множеств $ mathbb Z, mathbb Q, mathbb R_ $ или $ mathbb C_ $) с обычными операциями сложения полиномов и умножения на число из $ mathbb A_ $ не образует линейного пространства. Почему? — Потому что оно не является замкнутым относительно сложения: сумма полиномов

$$ f(x)=x^n -x+1 quad mbox quad g(x)=-x^n+x^-2 $$ не является полиномом $ n_ $-й степени. Но вот множество полиномов степени не выше $ n_ $ $$ mathbb P_n= left

$$ линейное пространство образует; только к этому множеству надо придать еще и тождественно нулевой полином 4) . Очевидными подпространствами $ mathbb P_ $ являются $ mathbb P_, mathbb P_1,dots,mathbb P_ $. Кроме того, подпространствами будут множество четных и множество нечетных полиномов степени не выше $ n_ $. Множество всевозможных полиномов

$$ mathbb P= bigcup_^ mathbb P_n $$ (без ограничения на степени) тоже образует линейное пространство.

Пример 7. Обобщением предыдущего случая будет пространство полиномов нескольких переменных $ x_1,dots, x_ $ степени не выше $ n_ $ с коэффициентами из $ mathbb A_ $. Например, множество линейных полиномов

$$ left< a_1x_1+dots+a_x_+b big| (a_1,dots,a_,b) in mathbb A^ right> $$ образует линейное пространство. Множество однородных полиномов (форм) степени $ n_ $ (с присоединением к этому множеству тождественно нулевого полинома) — также линейное пространство.

Видео:Базисные решения систем линейных уравнений (01)Скачать

Изоморфизм

Пусть имеются два линейных пространства разной природы: $ mathbb V_ $ с операцией $ +_ $ и $ mathbb W_ $ с операцией $ boxplus_ $. Может оказаться так, что эти пространства «очень похожи», и свойства одного получаются простым «переводом» свойств другого.

Говорят, что пространства $ mathbb V_ $ и $ mathbb W_ $ изоморфны если между множествами их элементов можно установить такое взаимно-однозначное соответствие, что если $ X_ leftrightarrow X^ $ и $ Y_ leftrightarrow Y^ $ то $ X+Y leftrightarrow X_^ boxplus Y^ $ и $ lambda X_ leftrightarrow lambda X^ $.

При изоморфизме пространств $ mathbb V_ $ и $ mathbb W_ $ нулевому вектору одного пространства будет соответствовать нулевой вектор другого пространства.

Пример. Пространство $ mathbb R^_ $ изоморфно пространству $ mathbb P_^ $. В самом деле, изоморфизм устанавливается соответствием $$ [a_1,dots,a_n] leftrightarrow a_1+a_2x+dots + a_nx^ .$$

Пример. Пространство $ mathbb R^ $ вещественных матриц порядка $ m_times n $ изоморфно пространству $ mathbb R_^ $. Изоморфизм устанавливается с помощью операции векторизации матрицы (матрица «вытягивается» в один столбец).

Пример. Пространство квадратичных форм от $ n_ $ переменных изоморфно пространству симметричных матриц $ n_ $-го порядка. Изоморфизм устанавливается соответствием, которое мы проиллюстрируем для случая $ n=3_ $:

$$ a_x_1^2+a_x_1x_2+a_x_1x_3+a_x_2^2+a_x_2x_3+a_x_3^2 leftrightarrow left( begin a_ & fraca_ & fraca_ \ fraca_ & a_ & fraca_ \ fraca_ & fraca_ & a_ end right) . $$

Видео:Образуют ли данные векторы базисСкачать

Линейная зависимость, базис, координаты

Линейной комбинацией системы векторов $ <X_1,dots,X_> $ называется произвольный вектор $$ alpha_1 X_1+dots+ alpha_m X_m $$ при каких-то фиксированных значениях скаляров $ alpha_, dots, alpha_ $.

Множество всевозможных линейных комбинаций системы векторов $ <X_1,dots,X_> $ $$ left< alpha_1 X_1+dots+ alpha_m X_m bigg| subset mathbb R right> $$ называется линейной оболочкой векторов $ X_1,dots,X_ $ и обозначается $ (X_1,dots,X_) $.

Теорема 1. Линейная оболочка векторов $ X_1,dots,X_ $ образует линейное подпространство пространства $ mathbb V_ $.

Пример. В пространстве $ mathbb P_ $ полиномов степеней $ le n_ ge 3 $ линейной оболочкой полиномов $ x,x^2,x^3 $ будет множество полиномов вида $ a_0x^3+a_1x^2+a_2x $, т.е. множество полиномов степеней $ le 3 $, имеющих корень $ lambda_=0 $. ♦

Система векторов $ < X_,dots,X_m > $ называется линейно зависимой (л.з.) если существуют числа $ alpha_,dots,alpha_m $, такие что хотя бы одно из них отлично от нуля и $$ alpha_1X_1+dots+alpha_mX_m=mathbb O $$ Если же это равенство возможно только при $ alpha_=0,dots,alpha_m=0 $, то система векторов называется линейно независимой (л.н.з.).

Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)

$$ f_1=(x_1+x_2+x_3)^2,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$ являются линейно зависимыми, поскольку $$ f_1-2,f_2-f_3 equiv 0 . $$ Полиномы $$ tilde f_1=x_1+x_2+x_3,quad f_2=x_1x_2+x_1x_3+x_2x_3,quad f_3=x_1^2+x_2^2+x_3^2 $$ не являются линейно зависимыми, но являются функционально зависимыми, поскольку $$ tilde f_1^2-2,f_2-f_3 equiv 0 . $$ ♦

Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.

б) Если система л.н.з., то и любая ее подсистема л.н.з.

в) При $ m>1 $ система $ <X_,dots,X_m> $ л.з. тогда и только тогда, когда по меньшей мере один ее вектор линейно выражается через остальные, т.е. существуют $ jin $ и константы $ gamma_,dots,gamma_, gamma_,dots,gamma_ $ такие, что $$ X_j=gamma_1X_1+dots+gamma_X_+ gamma_X_+dots + gamma_X_ .$$

Теорема 3. Если каждый из векторов системы $ < X_1,dots,X_> $ линейно выражается через векторы другой системы $ < B_,dots,B_k > $ с меньшим числом векторов: $ k ☞ ЗДЕСЬ.

Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.

Теорема 4. Системы векторов

$$ < X_1,dots,X_> quad mbox quad < Y_,dots,Y_k > $$ будут эквивалентными тогда и только тогда когда совпадают линейные оболочки этих систем: $$(X_1,dots,X_m)=(Y_1,dots,Y_k) . $$

Теорема 5. Если каждая из двух эквивалентных систем

$$ < X_1,dots,X_> quad mbox quad < Y_,dots,Y_k > $$ является л.н.з., то эти системы состоят из одинакового числа векторов: $ m=k_ $ .

Линейно независимая система векторов $ <X_>subset mathbb V $ называется базисом этого пространства если каждый $ Xin mathbb V $ можно представить в виде линейной комбинации указанных векторов: $$ X=sum_ alpha_j X_j . $$

При этом не подразумевается конечность системы, т.е. суммирование может распространяться на бесконечное число слагаемых. Так, например, пространство бесконечных строк (или последовательностей) $ left[a_,a_2,dots, right] $ имеет бесконечный базис, состоящий из векторов $$ [underbrace_j,0,dots , ] quad npu j in mathbb N . $$

В случае, когда базис пространства $ mathbb V_ $ конечен, пространство $ mathbb V_ $ называется конечномерным, а число векторов базиса тогда называется размерностью пространства $ mathbb V_ $ и обозначается 5) : $ dim mathbb V_ $. Также полагают, что размерность тривиального пространства, состоящего из одного только нулевого вектора, равна нулю: $ dim <mathbb O_>= 0 $.

Пример. Линейное пространство $ mtimes n_ $ матриц имеет размерность $ mn_ $. Так, для случая $ m_=3 ,n=2 $ в качестве базиса можно выбрать следующий набор матриц

$$ left( begin 1 & 0 \ 0 & 0 \ 0 & 0 end right) , left( begin 0 & 1 \ 0 & 0 \ 0 & 0 end right) , left( begin 0 & 0 \ 1 & 0 \ 0 & 0 end right) , left( begin 0 & 0 \ 0 & 1 \ 0 & 0 end right) , left( begin 0 & 0 \ 0 & 0 \ 1 & 0 end right) , left( begin 0 & 0 \ 0 & 0 \ 0 & 1 end right) . $$ ♦

Найти размерности подпространства симметричных и подпространства кососимметричных матриц порядка $ n_ $.

Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

под умножением цвета на положительное число $ k_ $ — увеличение в $ k_ $ раз яркости цвета

Анимация ☞ ЗДЕСЬ (1500 K, gif)

под умножением на $ (-1) $ — взятие дополнительного цвета. При этом оказывается, что совокупность всех цветов выражается линейно через три цвета: красный, зеленый и синий, т.е. образует трехмерное линейное пространство. (Точнее, некоторое тело в трехмерном пространстве, поскольку яркости цветов ограничены верхним порогом раздражения.) Исследование этого трехмерного тела всех цветов является важным орудием цветоведения. ♦

Если $ dim mathbb V=d_ $ и вектора $ X_1,dots,X_ $ являются базисными для $ mathbb V_ $, то разложение вектора $ X in mathbb V_ $ в сумму: $$ X=alpha_1 X_1+dots+ alpha_d X_d .$$ называется разложением вектора $ X_ $ по базису $ X_1,dots,X_ $; при этом числа $ alpha_1,dots, alpha_ $ называются координатами вектора $ X_ $ в данном базисе.

Теорема 6. Если $ dim mathbb V=d>0 $, то любая система из $ d_ $ линейно независимых векторов пространства образует базис этого пространства.

Доказательство. Пусть $ $ — л.н.з. система. Рассмотрим произвольный $ Xin mathbb V_ $. Если система $ $ л.н.з., то $ dim mathbb V ge d+1 $, что противоречит условию теоремы. Следовательно, система линейно зависима: $ alpha_0X+alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то из чисел $ _^ $ не равном нулю. Если $ alpha_0=0 $, то $ alpha_1Y_1+dots+alpha_dY_d=mathbb O $ при каком-то ненулевом коэффициенте. Это означает, что система $ $ линейно зависима, что противоречит предположению. Следовательно $ alpha_0ne 0 $, но тогда вектор $ X_ $ может быть представлен в виде линейной комбинации векторов $ Y_1,dots,Y_d $: $$X=- / Y_1-dots -/Y_d .$$ По определению, система $ $ является базисом $ mathbb V $. ♦

Теорема 7. Любой вектор $ X in mathbb V_ $ может быть разложен по фиксированному базису пространства единственным образом.

Очевидно, $ dim mathbb R^ = n $: строки из $ n_ $ элементов $$[1,0,0,dots,0], [0,1,0,dots,0], [0,0,1,dots,0], dots , [0,0,0,dots,1] $$ образуют базис этого пространства.

Имеются два способа задания линейных подпространств в $ mathbb R^_ $. Пусть $$ mathbb V_1 = (A_1,dots,A_k) quad npu subset mathbb R^n .$$ В разделе ☞ РАНГ установлено, что $$ dim mathbb V_1 = operatorname = operatorname (A) ,$$ где $ A_ $ — матрица, составленная из строк (столбцов) $ A_,dots,A_k $.

Пример. Найти базис подпространства

Решение. Ищем $$ operatorname left( begin 1 & 2 & 1 & 1 \ -1&0&-1&0 \ -1& 2 &-1 &1 \ 0& 1& 0 & 1 end right) $$ по методу окаймляющих миноров. Существует минор третьего порядка $$ left| begin 1 & 2 & 1 \ -1&0&0 \ 0& 1 & 1 end right| $$ отличный от нуля, а определитель самой матрицы равен нулю. Замечаем, что найденный отличный от нуля минор расположен в первой, второй и четвертой строках матрицы. Именно эти строки и образуют базис.

Ответ. Базис составляют, например, первая, вторая и четвертая строки.

Другим способом задания линейного подпространства в $ mathbb R^ $ может служить задание набора ограничений, которым должны удовлетворять векторы подпространства. Таким набором ограничений может являться, например, система уравнений $$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&0,\ a_x_1 +a_x_2+ldots+a_x_n &=&0,\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&0 endright. qquad iff qquad AX=mathbb O . $$ Какова размерность подпространства решений этой системы? На этот вопрос мы ответим сразу же, если вспомним определение фундаментальной системы решений (ФСР). Именно, ФСР — как набор линейно независимых решений, через которые линейно выражается любое решение системы однородных уравнений — является базисом подпространства этих решений.

Теорема 8. Множество решений системы однородных уравнений $ AX=mathbb O_ $ образует линейное подпространство пространства $ mathbb R^ $. Размерность этого подпространства равна $ n-operatorname (A) $, а фундаментальная система решений образует его базис.

Пример. В пространстве $ mathbb P_ $ полиномов степеней $ le n_ $ каноническим базисом можно взять систему мономов $ $, т.е. $ dim mathbb P_ =n+1 $. Координатами полинома

$$ f(x)=a_0+a_1x+a_2x^2+dots+a_nx^n $$ будут его коэффициенты. Можно выбрать и другой базис, например, $ $ при произвольном числе $ c_ $. Координатами полинома в этом базисе будут теперь коэффициенты формулы Тейлора: $$ f(x) equiv f(c)+ frac<f^(c)> (x-c) + frac<f^(c)> (x-c)^2+ dots + frac<f^(c)> (x-c)^ . $$

Найти координаты полинома

Теорема 9. Любое векторное пространство $ mathbb V_ $ размерности $ d_ $ изоморфно $ mathbb R^ $.

Доказательство. Изоморфизм можно установить следующим соответствием. Если $ $ — какой-то базис $ mathbb V_ $, то вектору $ X in mathbb V $ поставим в соответствие набор его координат в этом базисе: $$ X=x_1X_1+dots+x_d X_d Rightarrow X mapsto [x_1,dots,x_d]in mathbb R^d . $$ На основании теоремы $ 6 $, такое соответствие будет взаимно-однозначным, а проверка двух свойств изоморфизма тривиальна. ♦

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Критерии линейной зависимости

Теорема . Строки

$$ <(a_,dots,a_),dots, (a_,dots,a_)> subset mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ left|begin a_&dots & a_ \ dots & & dots \ a_& dots & a_ end right|=0 , . $$

Теорема . Строки

$$ <(a_,dots,a_),dots, (a_,dots,a_)> subset mathbb C^n $$ линейно зависимы тогда и только тогда, когда $$ operatorname A

$$ <(a_,dots,a_),dots, (a_,dots,a_)> subset mathbb R^n $$ линейно зависимы тогда и только тогда, когда $$ det (A^ A) = 0 , . $$ (Определитель в левой части можно интерпретировать как определитель Грама системы строк.)

Теорема . Аналитические на интервале $ ]a,b[ $ функции $ u_1(x),dots,u_n(x) $ линейно зависимы на $ ]a,b[ $ тогда и только тогда, когда их вронскиан

Относительный базис

В настоящем пункте $ mathbb V_1 $ обозначает линейное подпространство пространства $ mathbb V_ $, отличное от тривиального; обозначаем $ d_1=dim mathbb V_1 $.

Теорема. Произвольный базис подпространства $ mathbb V_1 $ можно дополнить до базиса пространства $ mathbb V_ $.

Доказательство. Пусть $ <X_1,dots,X_> $ — какой-то базис $ mathbb V_1 $. В пространстве $ mathbb V_ $ найдется вектор $ X_ $ такой, что система $ <X_1,dots,X_, X_> $ будет л.н.з. (В противном случае, $ dim mathbb V=d_1 $, что противоречит условию настоящего пункта.) Если $ d_1+1=d = dim mathbb V $, то, на основании теоремы 5 предыдущего пункта, требуемый базис построен. Если же $ d_1+1 ♦

Говорят, что система векторов $ $ линейно независима относительно подпространства $ mathbb V_1 $ пространства $ mathbb V_ $ если $$_ mbox quad alpha_1X_1+dots+alpha_k X_k in mathbb V_1 quad mbox quad alpha_1=dots=alpha_k=0 .$$

Теорема. Обозначим $ <Y_1,dots,Y_> $ — произвольный базис $ mathbb V_1 $. Система $ <X_,dots,X_k> $ л.н.з. относительно $ mathbb V_1 $ тогда и только тогда, когда система $ <Y_1,dots,Y_,X_1,dots,X_k> $ линейно независима.

Пример. Найти все значения параметра $ <coloralpha > $, при которых система

Решение. Базисом подпространства $ mathbb V_1 $ является произвольная ФСР заданной системы однородных уравнений, например $ <Y_1=[-1,2,1,0]^<^>, Y_2=[6,-5,0,1]^<^>> $. Теорема утверждает, что система $ $ л.н.з. относительно $ mathbb V_1 $ тогда и только тогда, когда система $ $ л.н.з. (в обычном понимании). Последнее равносильно тому, что матрица, составленная из этих векторов, должна иметь ранг равный $ 4_ $. $$operatorname left( begin 1 & 1 &-1 & 6 \ 2 & <coloralpha > & 2 & -5 \ <coloralpha > & 2 & 1 & 0 \ 1 & 1 & 0 & 1 end right)=4 iff left| begin 1 & 1 &-1 & 6 \ 2 & <coloralpha > & 2 & -5 \ <coloralpha > & 2 & 1 & 0 \ 1 & 1 & 0 & 1 end right|= <coloralpha >^2-10, <coloralpha > +16 ne 0 . $$

Ответ. $ <coloralpha >not in $.

Говорят, что система векторов $ $ образует базис пространства $ mathbb V_ $ относительно (или над) $ mathbb V_1 $ если она л.н.з. относительно $ mathbb V_1 $ и любой вектор $ Xin mathbb V_ $ можно представить в виде $$ X=c_1X_1+dots+c_kX_k+Y, quad mbox quad Yin mathbb V_1 . $$

Теорема. Обозначим $ < Y_1,dots,Y_> $ — произвольный базис подпространства $ mathbb V_1 $. Система $ $ образует базис $ mathbb V_ $ относительно $ mathbb V_1 $ тогда и только тогда, когда система $ < X_1,dots,X_k,Y_1,dots,Y_> $ образует базис $ mathbb V_ $.

Доказательство. Действительно, любой вектор $ Xin mathbb V_ $ выражается через векторы $ X_1,dots,X_k,Y_1,dots,Y_ $. По предыдущей теореме для линейной независимости этих векторов необходимо и достаточно относительной линейной независимости $ X_1,dots,X_k $. ♦

Базис $ mathbb V_ $ строится дополнением базиса $ mathbb V_1 $ векторами $ X_1,dots,X_k $ линейно независимыми относительно $ mathbb V_1 $. Поэтому $$_ mbox = dim mathbb V — dim mathbb V_1 .$$

Это число называется коразмерностью 6) подпространства $ mathbb V_1 $ в пространстве $ mathbb V $.

Видео:Базисы суммы и пересечения линейных подпространствСкачать

Сумма и пересечение линейных подпространств

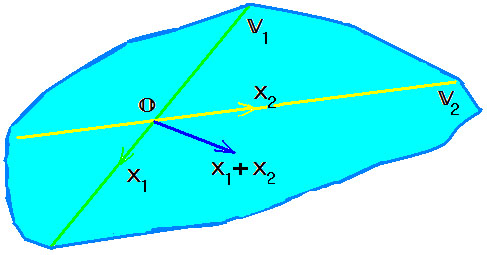
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_ $. Множество $$ mathbb V_1+ mathbb V_2 = left$$ называется суммой, а множество $$ mathbb V_1 cap mathbb V_2 = left$$ — пересечением подпространств $ mathbb V_1 $ и $ mathbb V_2 $. Аналогично определяется сумма и пересечение произвольного количества подпространств.

Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.

Теорема. $ mathbb V_1+ mathbb V_2 $ и $ mathbb V_1 cap mathbb V_2 $ являются подпространствами линейного пространства $ mathbb V_ $.

Докажите, что $ mathbb V_1+ mathbb V_2 $ — это подпространство минимальной размерности, содержащее как $ mathbb V_1 $, так и $ mathbb V_2 $.

Теорема. Имеет место формула:

$$ dim , mathbb V_1 + dim , mathbb V_2=dim , (mathbb V_1 cap mathbb V_2) + dim , (mathbb V_1 + mathbb V_2) . $$

Доказательство ☞ ЗДЕСЬ.

Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:

$$dim , mathbb V_1 + dim , mathbb V_2 + dim , mathbb V_3 — $$ $$ -left + $$ $$+ dim , (mathbb V_1 cap mathbb V_2 cap mathbb V_3) =dim , (mathbb V_1 + mathbb V_2 + mathbb V_3) ?$$

Теорема. Имеет место формула:

Пример. Найти базис суммы и размерность пересечения

$$mathbb V_1=left( left[ begin 0 \1 \ 1 \ 1 end right] , left[ begin 1 \1 \ 1 \ 2 end right] , left[ begin -2 \0 \ 1 \ 1 end right] right) quad mbox quad mathbb V_2=left( left[ begin -1 \3 \ 2 \ -1 end right] , left[ begin 1 \1 \ 0 \ -1 end right] right) $$

Решение. Действуя согласно предыдущей теореме, составляем матрицу из всех векторов $$ left( begin 0 & 1 & -2 & -1 & 1 \ 1 & 1 & 0 & 3 & 1 \ 1 & 1 & 1 & 2 & 0 \ 1 & 2 & 1 & -1 & -1 end right) $$ и ищем ее ранг методом окаймляющих миноров. Имеем: $ operatorname = 3 $ при ненулевом миноре матрицы расположенном в первых трех ее столбцах.

Ответ. Базис $ mathbb V_1 + mathbb V_2 $ составляют векторы $ X_1,X_2,X_3 $; $ dim , (mathbb V_1 cap mathbb V_2) = 3+2 — 3 =2 $.

Алгоритм нахождения базиса $ (X_1,dots,X_m) cap (Y_1,dots,Y_) $ проиллюстрируем на примере.

Пример. Найти базис $ mathbb V_1 cap mathbb V_2 $ при

$$ begin mathbb V_1= left( left[ begin 1 \ -1 \ 1 \ -1 \ 1 end right],, left[ begin 1 \ 2 \ 1 \ 2 \ 1 end right],, left[ begin 0 \ 1 \ 0 \ 1 \ 0 end right] right) \ _ qquad qquad quad X_1 quad quad X_2 quad quad X_3 end , begin mathbb V_2= left( left[ begin 1 \ 0 \ 0 \ 0 \ 1 end right],, left[ begin 1 \ 1 \ 0 \ 1 \ 1 end right],, left[ begin 0 \ 1 \ 1 \ 1 \ 0 end right] right) \ _ quad qquad qquad Y_1 qquad Y_2 quad quad Y_3 end . $$

Решение. 1. Сначала найдем базисы каждого из подпространств: $$dim mathbb V_1=2, mathbb V_1=mathcal L(X_1, X_2) ; dim mathbb V_2=3, mathbb V_2=mathcal L(Y_1, Y_2, Y_3) . $$

2. Произвольный вектор $ Zin mathbb R^5 $, принадлежащий $ mathbb V_1 cap mathbb V_2 $, должен раскладываться по базису каждого из подпространств: $$Z=alpha_1 X_1 + alpha_2 X_2= beta_1 Y_1 + beta_2 Y_2 + beta_3 Y_3 .$$ Для определения неизвестных значений координат составляем систему уравнений $$ begin qquad X_1 X_2 \ qquad <colordownarrow> <colordownarrow> \ left( begin 1 & 1 & -1 & &-1 & & 0 \ -1 & 2 & 0 & & -1 & & -1 \ 1 & 1 & 0 & & 0 & & -1 \ -1 & 2 & 0 & & -1 & & -1 \ 1 & 1 & -1 & & -1 & & 0 end right) \ qquad qquad qquad <coloruparrow> qquad <coloruparrow> qquad quad <coloruparrow> \ quad qquad qquad -Y_1 quad — Y_2 quad -Y_3 end left( begin alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3 end right)= mathbb O_ $$ и решаем ее по методу Гаусса с нахождением фундаментальной системы решений: $$ left( begin 1 & 1 & -1 & -1 & 0 \ 0 & 3 & -1 & -2 & -1 \ 0 & 0 & 1 & 1 & -1 \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 end right) left( begin alpha_1 \ alpha_2 \ beta_1 \ beta_2 \ beta_3 end right)= mathbb O quad Rightarrow qquad mbox qquad begin alpha_1 & alpha_2 & beta_1 & beta_2 & beta_3 \ hline -1/3 & 1/3 & -1 & 1 & 0 \ 1/3 & 2/3 & 1 & 0 & 1 end $$

3. Получившиеся значения координат позволяют выразить базис пересечения — либо через базис подпространства $ mathbb V_1 $ (если использовать полученные значения для $ alpha_1,alpha_2 $), либо через базис подпространства $ mathbb V_2 $ (если использовать $ beta_1,beta_2, beta_3 $). Например, $$ Z_1=-1/3 X_1 + 1/3 X_2 = [0,1,0,1,0]^<^>, $$ $$ Z_2=1/3 X_1 + 2/3 X_2 = [1,1,1,1,1]^<^> . $$

Найти базисы суммы и пересечения подпространств

Решение ☞ ЗДЕСЬ.

Прямая сумма линейных подпространств

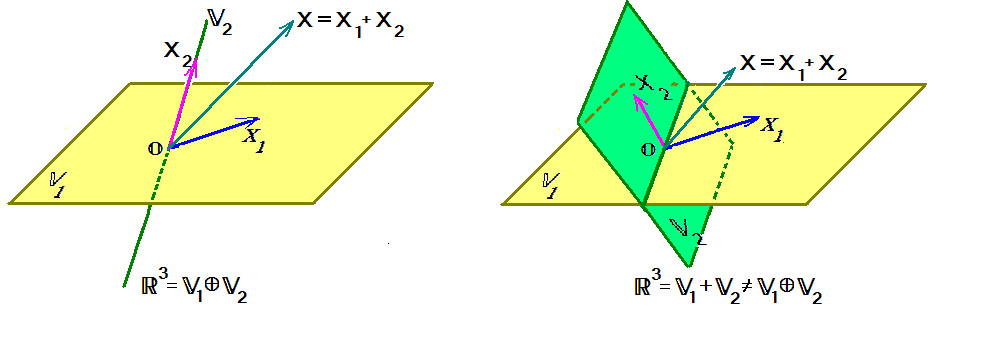
Пусть $ mathbb V_1 $ и $ mathbb V_2 $ — подпространства линейного пространства $ mathbb V_ $. Говорят, что $ mathbb V_ $ раскладывается в прямую сумму подпространств $ mathbb V_1 $ и $ mathbb V_2 $ если любой вектор $ Xin mathbb V_ $ может быть представлен в виде $ X=X_1+X_2 $, где $ X_1in mathbb V_1,X_2in mathbb V_2 $ и такое представление единственно. Этот факт записывают: $ mathbb V= mathbb V_1 oplus mathbb V_2 $. Вектор $ X_ $ называется проекцией вектора $ X_ $ на подпространство $ mathbb V_1 $ параллельно подпространству $ mathbb V_ $.

Пример. Линейное пространство квадратных матриц порядка $ n_ $ раскладывается в прямую сумму подпространств: подпространства симметричных матриц и подпространства кососимметричных матриц. В самом деле, для матрицы $ A_ $ справедливо разложение

$$A=frac left(A+A^ right) + frac left(A-A^ right) $$ и в правой части первая скобка дает симметричную матрицу, а вторая — кососимметричную. Покажите, что не существует иного разложения матрицы $ A_ $ в сумму симметричной и кососимметричной.

Теорема. Пусть $ mathbb V=mathbb V_1 + mathbb V_2 $. Эта сумма будет прямой тогда и только тогда, когда подпространства $ mathbb V_1 $ и $ mathbb V_2 $ имеют тривиальное пересечение:

$$mathbb V_1 cap mathbb V_2= .$$

Доказательство. Необходимость. Пусть сумма $ mathbb V_1 + mathbb V_2 $ — прямая, но существует вектор $ Xne mathbb O $, принадлежащий $ mathbb V_1 cap mathbb V_2 $. Но тогда и вектор $ (-X) $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Для нулевого вектора $ mathbb O $ получаем два представления в виде суммы проекций на подпространства: $$ mathbb O = mathbb O + mathbb O = X+ (-X) , . $$ Это противоречит понятию прямой суммы.

Достаточность. Если $ mathbb V_1 cap mathbb V_2= $, но существует вектор $ X in mathbb V_1 + mathbb V_2 $, имеющий два различных разложения в сумму проекций $$ X=X_1+X_2 =Y_1+ Y_2 quad npu quad subset mathbb V_1, subset mathbb V_2, $$ то $$ (X_1-Y_1)+(X_2-Y_2) =mathbb O quad Rightarrow quad X_1-Y_1=Y_2-X_2 , , $$ т.е. вектор $ X_1-Y_1 $ принадлежит $ mathbb V_1 cap mathbb V_2 $. Но, по предположению, $ mathbb V_1 cap mathbb V_2= $, следовательно, $ X_1-Y_1=mathbb O $, но тогда и $ Y_2-X_2=mathbb O $. ♦

Сумма $ mathbb V=mathbb V_1 + mathbb V_2 $ будет прямой тогда и только тогда, когда базис $ mathbb V_ $ может быть получен объединением базисов $ mathbb V_ $.

Пример [2]. Доказать, что сумма подпространств

$$mathbb V_1=left( left[ begin 2 \3 \ 11 \ 5 end right] , left[ begin 1 \1 \ 5 \ 2 end right] , left[ begin 0 \1 \ 1 \ 1 end right] right) quad mbox quad mathbb V_2=left( left[ begin 2 \1 \ 3 \ 2 end right] , left[ begin 1 \1 \ 3 \ 4 end right] , left[ begin 5 \2 \ 6 \ 2 end right] right) $$ будет прямой и найти проекции вектора $ Z=[2,0,0,3]^ $ на эти подпространства.

Решение. Базисы $ mathbb V_1 $ и $ mathbb V_2 $ составляют соответственно системы $ $ и $ $, т.е. $ dim , mathbb V_1=dim , mathbb V_2 =2 $. На основании следствия достаточно установить, что объединенная система $ $ л.н.з. Для этого достаточно проверить, что определитель матрицы $$ A=left( begin 1 & 0 & 2 & 1 \ 1 & 1 & 1 & 1 \ 5 & 1 & 3 & 3 \ 2 & 1 & 2 & 4 end right) $$ отличен от нуля. Поскольку это условие выполнено, то сумма $ mathbb V_1 + mathbb V_2 $ — прямая и базис этой суммы состоит из взятых векторов. Для нахождения разложения вектора $ X_ $ по этому базису решаем систему уравнений $$A left[ begin alpha_2 \ alpha_3 \ beta_1 \ beta_2 end right] = Z $$ и получаем единственное решение: $ alpha_2=-1,, alpha_3=-1,, beta_1 =1, , beta_2=1 $. Разложение $ Z=Z_1+Z_2 $ составляют векторы $ Z_1=alpha_2 X_2+alpha_3 X_3 $ и $ Z_2=beta_1 Y_1+beta_2 Y_2 $.

Линейные многообразия

Пусть $ mathbb V_1 $ — линейное подпространство пространства $ mathbb V_ $, а $ X_ $ — произвольный фиксированный вектор из $ mathbb V_ $. Множество $$ mathbb M = X_0+ mathbb V_1 = left $$ называется линейным многообразием (порожденным подпространством $ mathbb V_1 $). Размерностью этого многообразия называется размерность порождающего его подпространства: $ dim mathbb M = dim mathbb V_1 $. В случае $ 1 ☞ ОБЩЕЕ РЕШЕНИЕ: если система совместна, то ее общее решение можно представить как сумму какого-то одного ее решения и общего решения соответствующей однородной системы $ AX= mathbb O $. Таким образом, многообразие решений неоднородной системы $ AX= $ допускает «параметрическое представление»: $$mathbb M=X_0+ (X_1,dots,X_<n->)= $$ $$=left<X_0+t_1 X_1+dots+ t_<n-> X_<n-> mid (t_1,dots, t_<n->) in mathbb R^<n-> right> ; $$ здесь $ X_ $ означает частное решение системы (т.е. $ AX_0= $),

$ <X_1,dots,X_<n->> $ — ФСР для системы $ AX= mathbb O $,

а $ mathfrak r= operatorname A= operatorname [Amid mathcal B] $.

Получаем, следовательно, $ (n-) $-мерную плоскость в $ mathbb R^n $, a в случае $ (n-)=1 $ — прямую $$mathbb M=X_0+tX_1 quad npu t in mathbb R ; $$ в последнем случае вектор $ X_ $ называют направляющим вектором этой прямой.

Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.